Презентация на тему: Четырехугольники 8 класс

Автор: учитель математики Комлякова Ксения ГеннадьевнаГБОУ Гимназия №105, г. Санкт-Петербург Урок «Четырехугольники» геометрия 8 класс

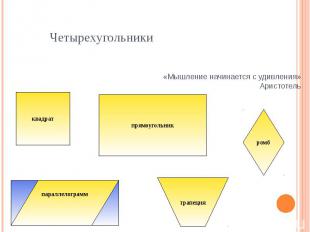
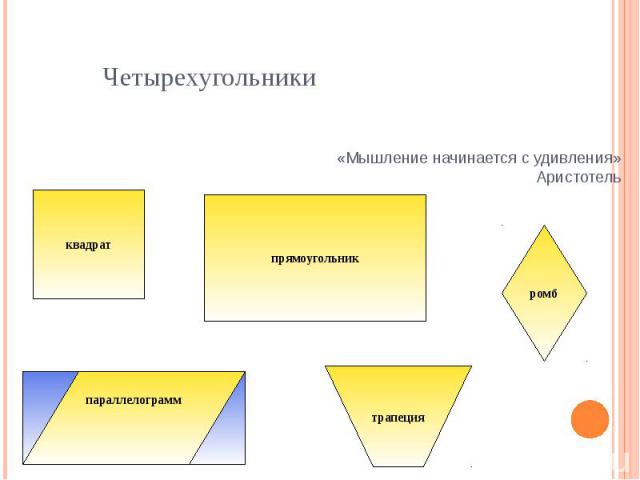
Четырехугольники «Мышление начинается с удивления»Аристотель

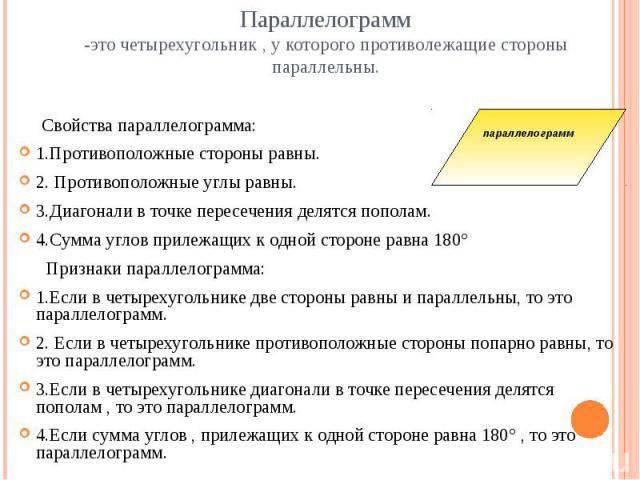
Параллелограмм-это четырехугольник , у которого противолежащие стороны параллельны. Свойства параллелограмма:1.Противоположные стороны равны.2. Противоположные углы равны.3.Диагонали в точке пересечения делятся пополам.4.Сумма углов прилежащих к одной стороне равна 180° Признаки параллелограмма:1.Если в четырехугольнике две стороны равны и параллельны, то это параллелограмм.2. Если в четырехугольнике противоположные стороны попарно равны, то это параллелограмм.3.Если в четырехугольнике диагонали в точке пересечения делятся пополам , то это параллелограмм.4.Если сумма углов , прилежащих к одной стороне равна 180° , то это параллелограмм.

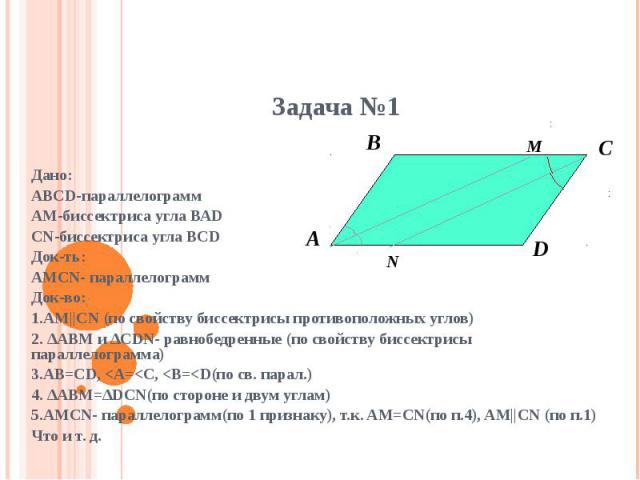
АВСД - параллелограмм. Луч АМ -биссектриса угла ВАД. Луч СN-биссектриса угла ВСД . Докажите , что АNСМ-параллелограмм.

Прямоугольник- это параллелограмм, у которого все углы прямые Свойства прямоугольника:1-4 свойства параллелограмма.5.Диагонали прямоугольника равны. Признаки прямоугольника:1.Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.2.Если в параллелограмме один угол прямой, то это прямоугольник.3. Четырехугольник, у которого три прямых угла -прямоугольник.

Задача №2 Диагонали прямоугольника ABCD пересекаются в точке O. Докажите, что треугольники AOB и AOD – равнобедренные.

Ромб – это параллелограмм, у которого все стороны равны. Свойства ромба:1-4 параллелограмма5.Диагонали ромба взаимно перпендикулярны.6.Диагонали ромба делят углы пополам. Признаки ромба:1. Если в параллелограмме диагонали взаимно-перпендикулярны, то это ромб.2.Если в параллелограмме диагонали делят углы пополам, то это ромб.3.Если в параллелограмме две смежные стороны равны , то это ромб.4.Четырехугольник, у которого все стороны равны -ромб.

Задача №3Верно ли , что четырехугольник , у которого диагонали взаимно-перпендикулярны, является ромбом?

Квадрат – это параллелограмм, у которого все стороны равны и все углы прямые.Квадрат -это прямоугольник, у которого все стороны равны.Квадрат -это ромб, у которого все углы прямые. Свойства квадрата:1-4 свойства параллелограмма.5 свойство прямоугольника.5,6 свойства ромба. Признаки квадрата:1. Если диагонали прямоугольника пересекаются под прямым углом, то это квадрат.2. Если у ромба один угол прямой, то это квадрат.3. Если в четырехугольнике диагонали равны, взаимно -перпендикулярны, точкой пересечения делятся пополам, то это квадрат.

В прямоугольном треугольнике проведена биссектриса прямого угла. Через точку пересечения этой биссектрисы с гипотенузой проведены прямые, параллельные катетам. Докажите, что полученный четырехугольник – квадрат.

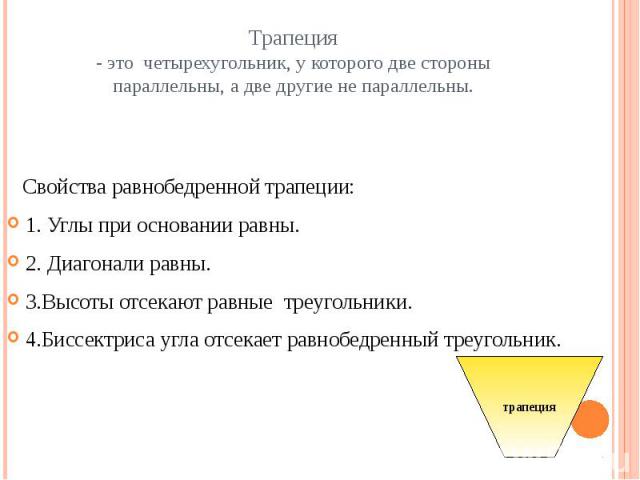
Трапеция- это четырехугольник, у которого две стороны параллельны, а две другие не параллельны. Свойства равнобедренной трапеции:1. Углы при основании равны.2. Диагонали равны.3.Высоты отсекают равные треугольники.4.Биссектриса угла отсекает равнобедренный треугольник.

Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 120°.

Самостоятельная работа №1. АВСД - параллелограмм . Луч АМ- биссектриса угла ВАД. Луч СN- биссектриса угла ВСД. Докажите, что АNСМ-параллелограмм.(5 б.)№2. Диагонали прямоугольника ABCD пересекаются в точке O. Докажите, что треугольники AOB и AOD – равнобедренные.(2 б.)№3. Верно ли, что четырехугольник, у которого диагонали взаимно-перпендикулярны, является ромбом?(2 б.)№4. В прямоугольном треугольнике проведена биссектриса прямого угла. Через точку пересечения этой биссектрисы с гипотенузой проведены прямые, параллельные катетам. Докажите, что полученный четырехугольник – квадрат.(5 б.)№5. Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 120°.(4 б.)

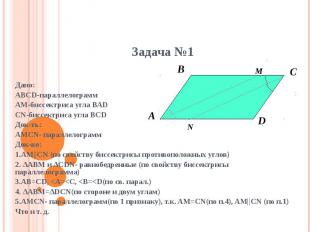
Дано:АВСD-параллелограммАМ-биссектриса угла ВАDCN-биссектриса угла BCDДок-ть:AMCN- параллелограммДок-во:1.AM||CN (по свойству биссектрисы противоположных углов)2. ∆ABM и ∆CDN- равнобедренные (по свойству биссектрисы параллелограмма)3.AB=CD, <A=<C, <B=<D(по св. парал.)4. ∆ABM=∆DCN(по стороне и двум углам)5.AMCN- параллелограмм(по 1 признаку), т.к. AM=CN(по п.4), AM||CN (по п.1)Что и т. д.

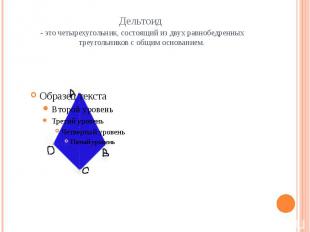
Дельтоид - это четырехугольник, состоящий из двух равнобедренных треугольников с общим основанием.