Презентация на тему: Чертеж прямой. Положение прямой в пространстве

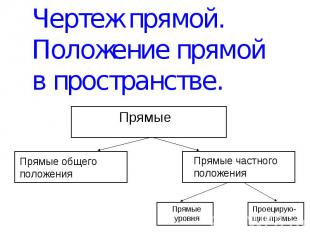
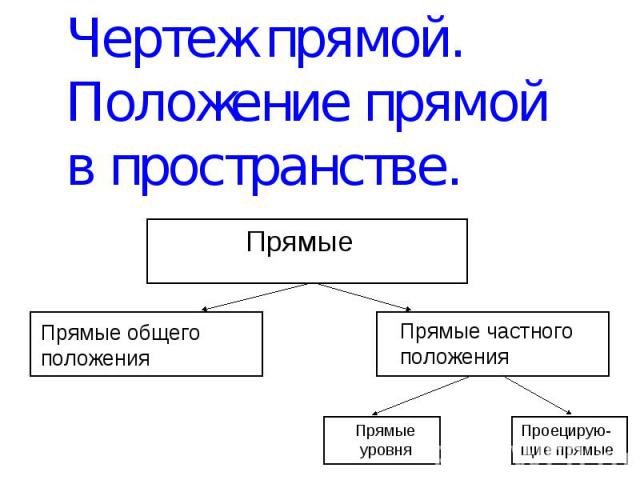
Чертеж прямой. Положение прямой в пространстве. Прямые Прямые общего положения Прямые частного положения Прямые уровня Проецирую-щие прямые

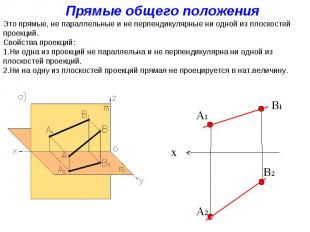
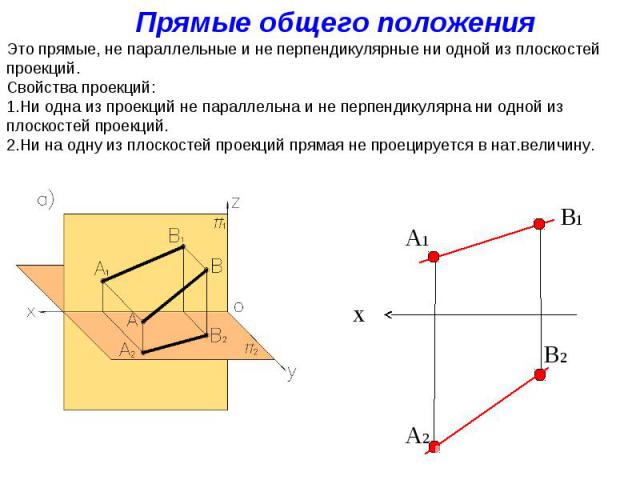
Прямые общего положения Это прямые, не параллельные и не перпендикулярные ни одной из плоскостей проекций. Свойства проекций: Ни одна из проекций не параллельна и не перпендикулярна ни одной из плоскостей проекций. Ни на одну из плоскостей проекций прямая не проецируется в нат.величину. A1 A2 B1 B2 x

m1 x m2

Прямые уровня – это прямые, параллельные одной из плоскостей проекций

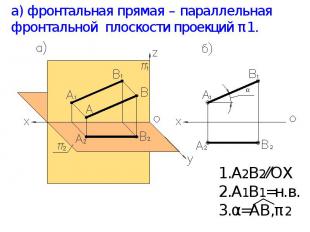
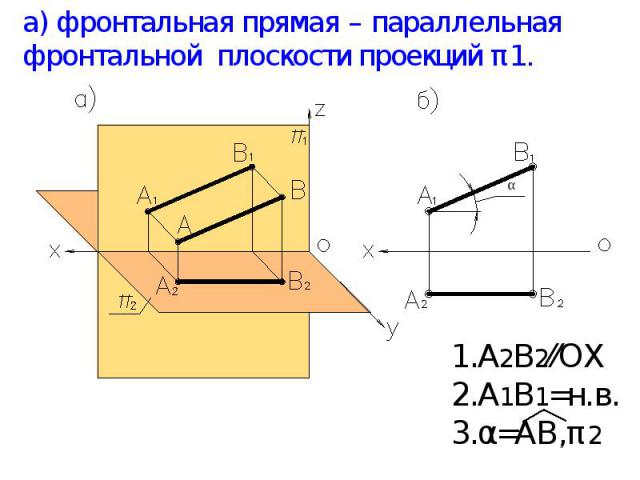
а) фронтальная прямая – параллельная фронтальной плоскости проекций π1. А2В2⁄⁄ОХ А1В1=н.в. α=АВ,π2

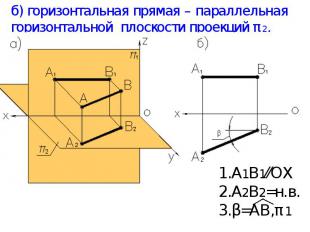
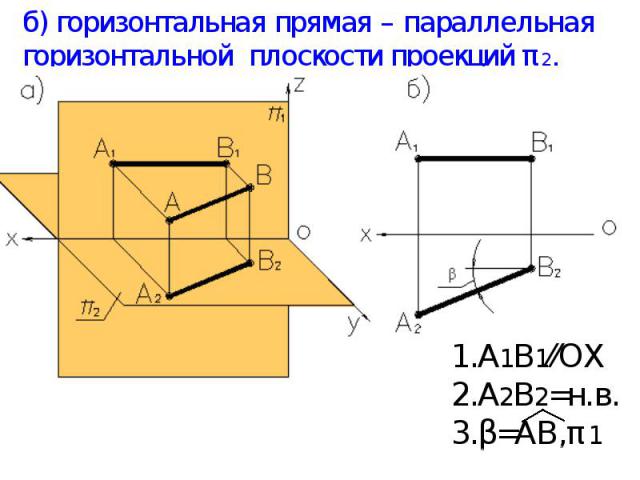
б) горизонтальная прямая – параллельная горизонтальной плоскости проекций π2. А1В1⁄⁄ОХ А2В2=н.в. β=АВ,π1

Проецирующие прямые- это прямые, перпендикулярные одной из плоскостей проекций.

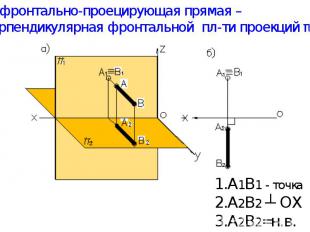
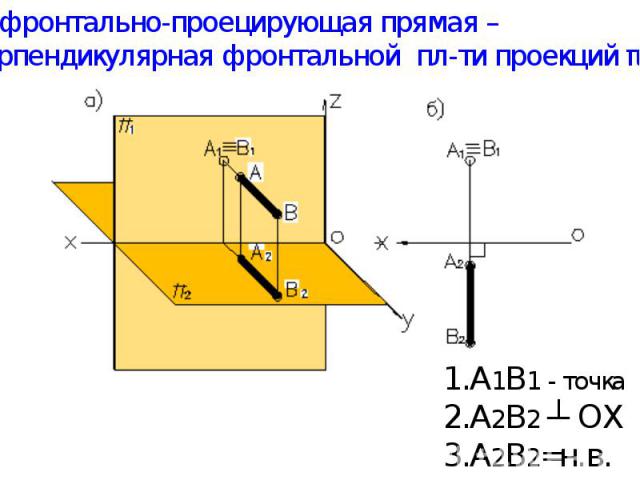
а) фронтально-проецирующая прямая – перпендикулярная фронтальной пл-ти проекций π1. А1В1 - точка А2В2 ┴ ОХ А2В2=н.в.

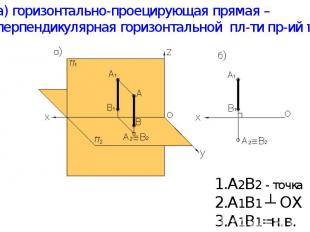
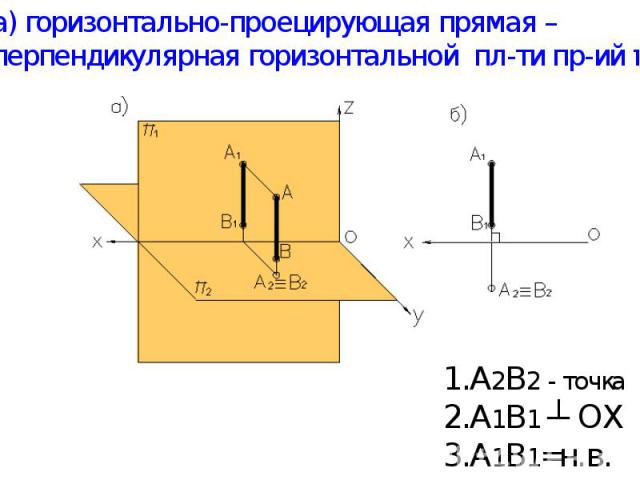
а) горизонтально-проецирующая прямая – перпендикулярная горизонтальной пл-ти пр-ий π2. А2В2 - точка А1В1 ┴ ОХ А1В1=н.в.

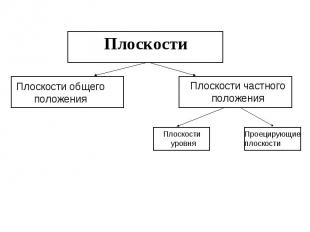
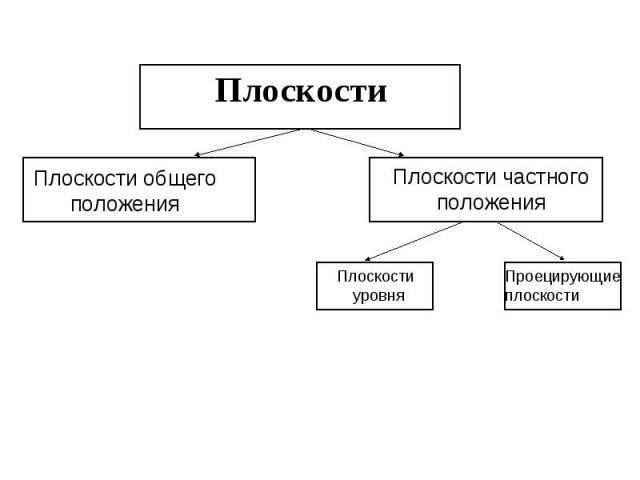
Плоскости Плоскости общего положения Плоскости частного положения Плоскости уровня Проецирующие плоскости

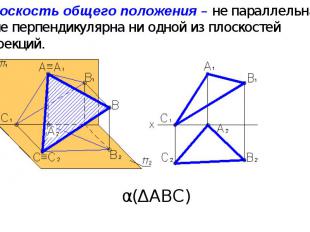
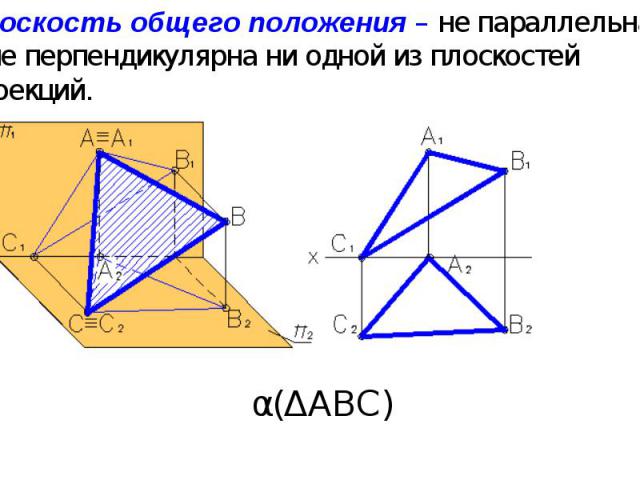
Плоскость общего положения – не параллельна и не перпендикулярна ни одной из плоскостей проекций. α(ΔАВС)

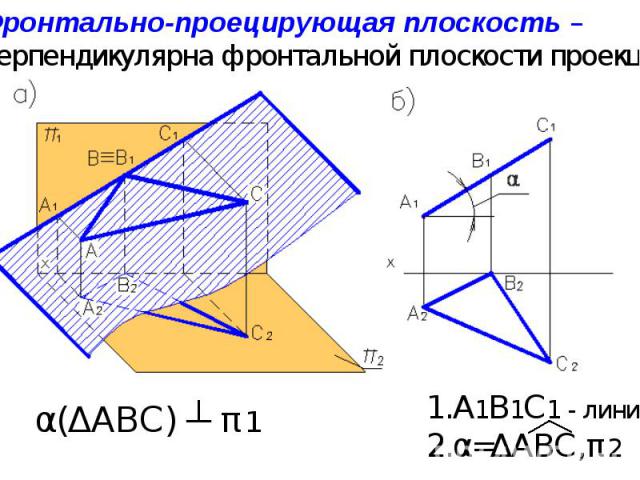
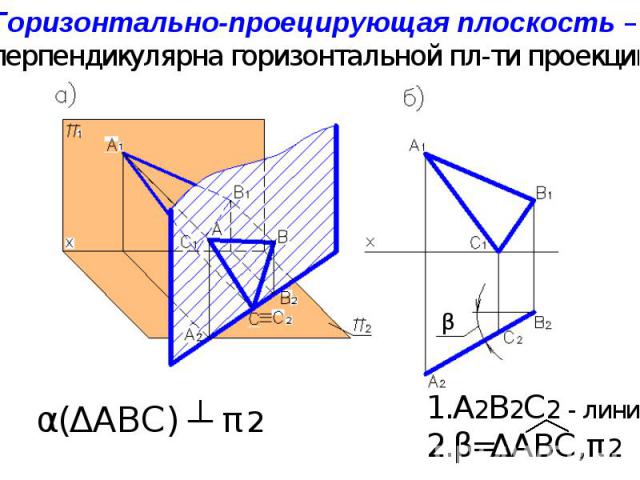
Проецирующая плоскость- перпендикулярна одной из плоскостей проекций.

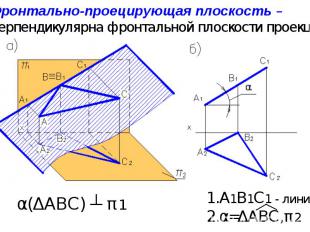
А1В1С1 - линия α=ΔАВС,π2 Фронтально-проецирующая плоскость – перпендикулярна фронтальной плоскости проекций. α(ΔАВС) ┴ π1

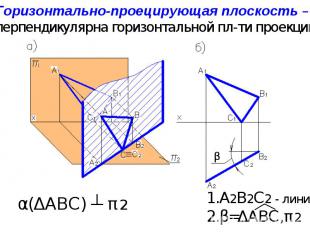
А2В2С2 - линия β=ΔАВС,π2 Горизонтально-проецирующая плоскость – перпендикулярна горизонтальной пл-ти проекций. α(ΔАВС) ┴ π2 β

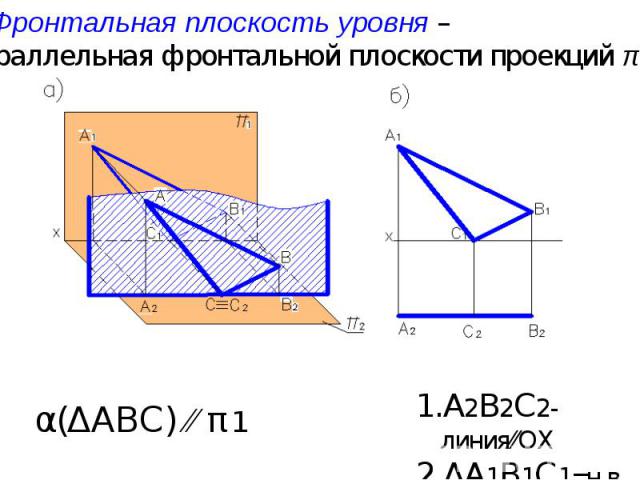
Плоскости уровня – это плоскости, параллельные одной из плоскостей проекций.

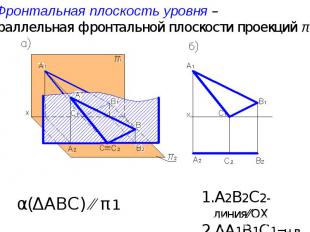
Фронтальная плоскость уровня – параллельная фронтальной плоскости проекций π1 А2В2С2-линия⁄⁄ОХ ΔА1В1С1=н.в. α(ΔАВС) ⁄⁄ π1

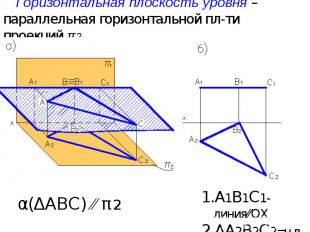
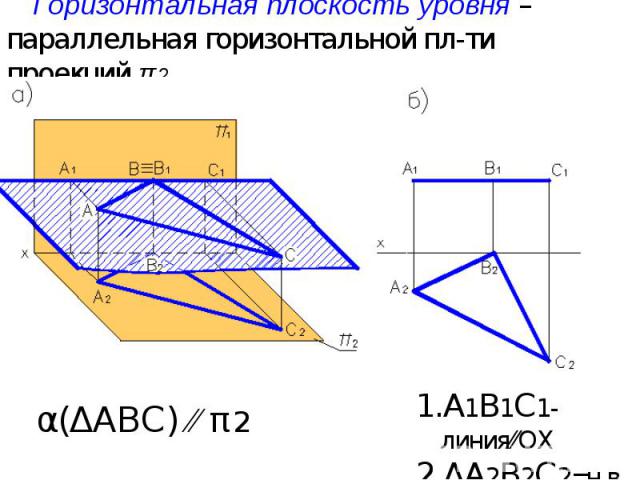
Горизонтальная плоскость уровня – параллельная горизонтальной пл-ти проекций π2 А1В1С1-линия⁄⁄ОХ ΔА2В2С2=н.в. α(ΔАВС) ⁄⁄ π2

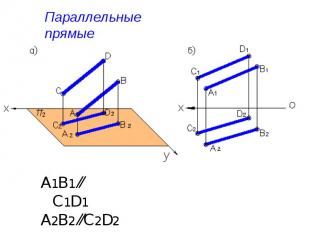
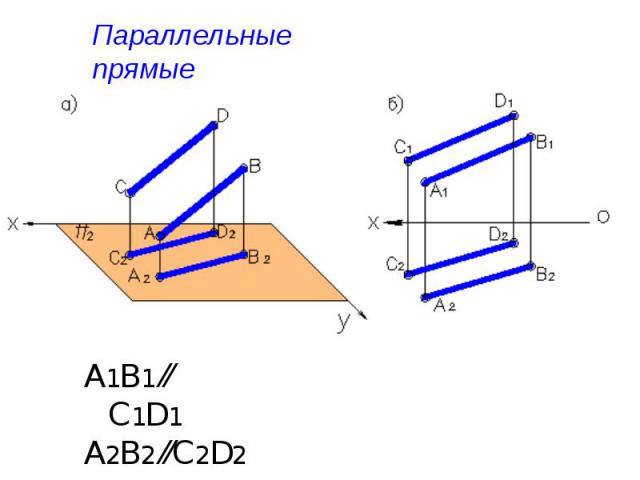
Параллельные прямые А1В1 ⁄⁄ C1D1 А2В2 ⁄⁄C2D2

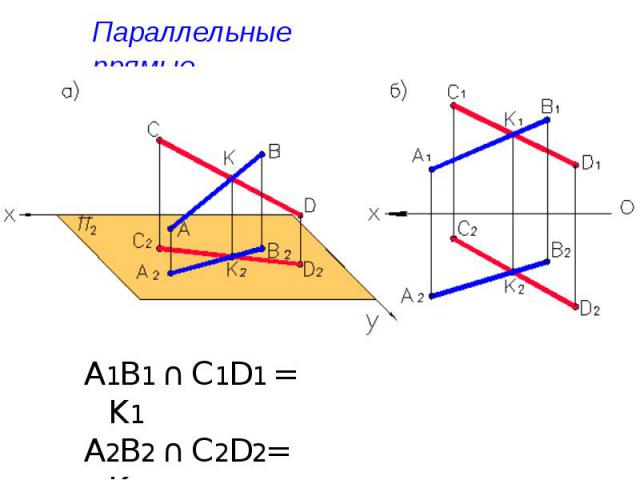
Параллельные прямые А1В1 ∩ C1D1 = K1 А2В2 ∩ C2D2= K2

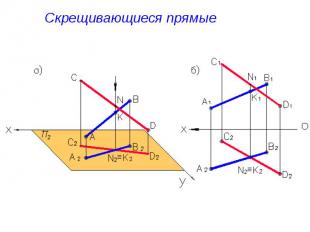
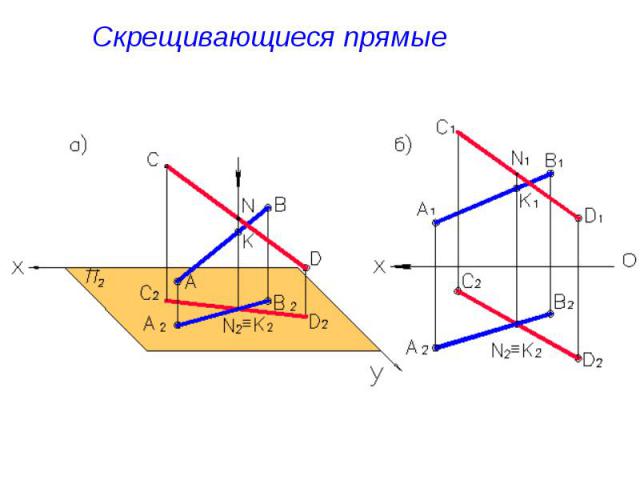
Скрещивающиеся прямые