Презентация на тему: Векторы. Модуль вектора. Равенство векторов. Сложение векторов

Векторы. Модуль вектора. Равенство векторов. Сложение векторовПреподаватель: Никонорова Е.А.

Направления отрезка

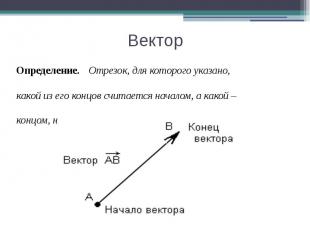
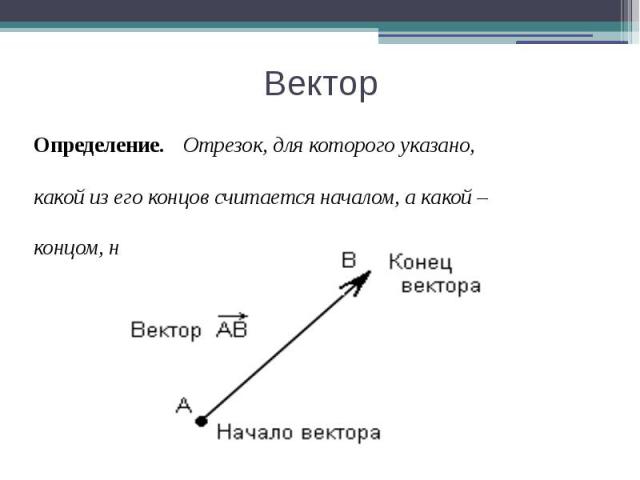
Вектор Определение. Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором.

Вектор Векторы обозначают: или

Нулевой вектор Определение. Нулевой вектор – это вектор,начало и конец которого совпадают. Направлениенулевого вектора считается неопределенным.

Длина вектора Определение. Длиной ненулевого вектора называется длина отрезка АВ. Длина вектора (вектора ) обозначается так: ( ). Длина нулевого вектора: = 0.

Коллинеарные векторы Определение. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. – коллинеарны

Сонаправленные векторы Определение. Два ненулевых вектора называютсясонаправленными, если они коллинеарны инаправлены в одну сторону. – сонаправленные векторы – противоположно направленные векторы

Противоположные векторы Определение. Два ненулевых вектора называются противоположными друг другу, если они имеют одинаковые модули, коллинеарны и противоположно направленные. противоположно направленные противоположные векторы

Равные векторы Определение. Векторы называются равными, если они сонаправленны и их длины равны.Теорема. От любой точки можно отложить вектор, равный данному, и притом только один. , так как

Правило треугольника Определение. Суммой двух векторов и называетсятретий вектор , соединяющий начало первого слагаемоговектора с концом второго при условии, что начало второго слагаемого совмещено с концом первого.

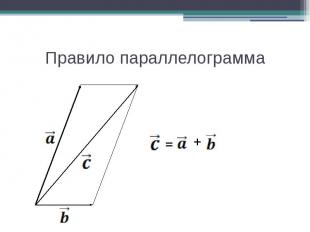
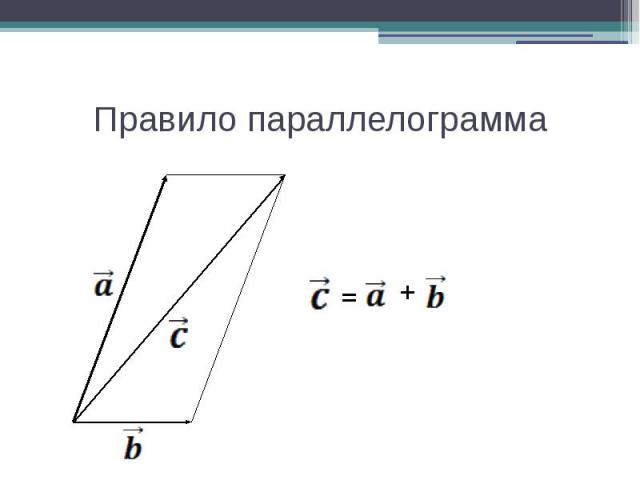
Правило параллелограмма

Правило многоугольника Определение. Суммой нескольких векторов , , , ,….,является вектор , соединяющий начало первогослагаемого вектора , с концом последнего слагаемоговектора , при условии, что начало каждогопоследующего вектора совмещено с концомпредыдущего.

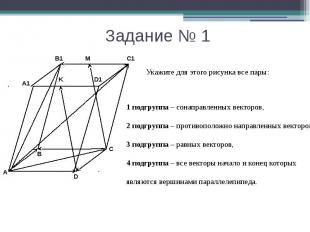
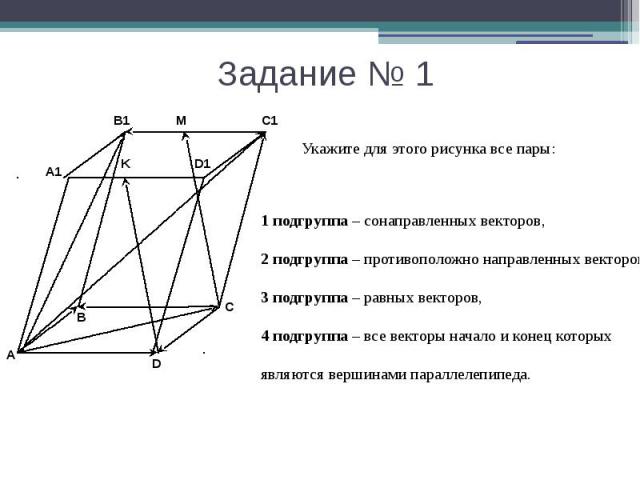
Задание № 1 1 подгруппа – сонаправленных векторов,2 подгруппа – противоположно направленных векторов,3 подгруппа – равных векторов,4 подгруппа – все векторы начало и конец которых являются вершинами параллелепипеда.

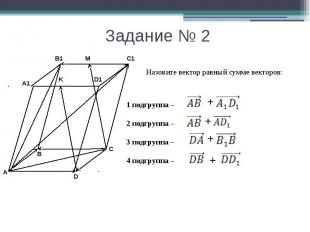
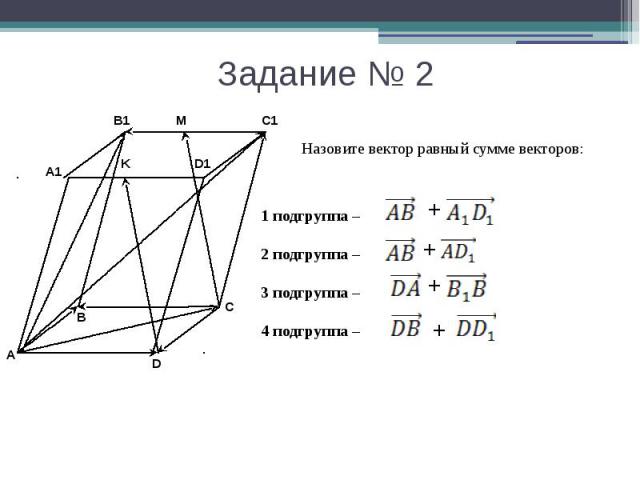
Задание № 2 Назовите вектор равный сумме векторов: 1 подгруппа – 2 подгруппа – 3 подгруппа – 4 подгруппа –

Что такое вектор?Что понимают под длинной или модулем вектора?Какие векторы называются коллинеарными?Какие векторы называются сонаправленными?Какие векторы называют равными?Как построить сумму двух векторов? Какие правила сложения двух векторов мы сегодня изучили?Как называется правило сложения более двух векторов?

Домашнее задание Сборник задач по математике А.А. Дадаян:№ 3.2.№ 3.3.№ 3.5.

Спасибо за внимание!