Презентация на тему: Решение уравнений, содержащих модуль

Решение уравнений, содержащих модуль

Проверка домашнего задания №1110(в,г) При b=0 |b |-2= |0 |-2 =0-2=-2; При d= 2 -1 |d |+1= | 2-1 |+1= 2-1+1= 2 №1111(в,г) При m=-5/7,n=4 |m+n |:2= |-5/7+4 |:2=23/7:2==23/14. При p=-1,2, q=8 |p-q |:4= |-1,2-8 |:4=9,2:4=2,3. №1132 а)на отрезке [2;6] унаим.=-2,унаиб.= 2; б) на луче [-1;+∞) унаим.= -4,унаиб. не сущ.; в)на луче (-∞;0] унаим.= -4,унаиб. не сущ.; г)на отрезке [-4;5] унаим.= -4,унаиб.= 1;

Проверим знания! 1. Дайте определение модуля 2. Верно ли, что |-5 |=5; |8 |=-8; |5,7|=5,7? 3. С какими свойствами модуля вы знакомы?

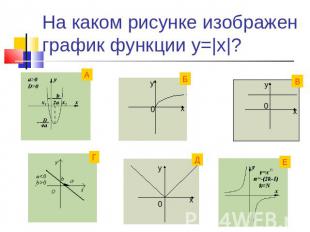
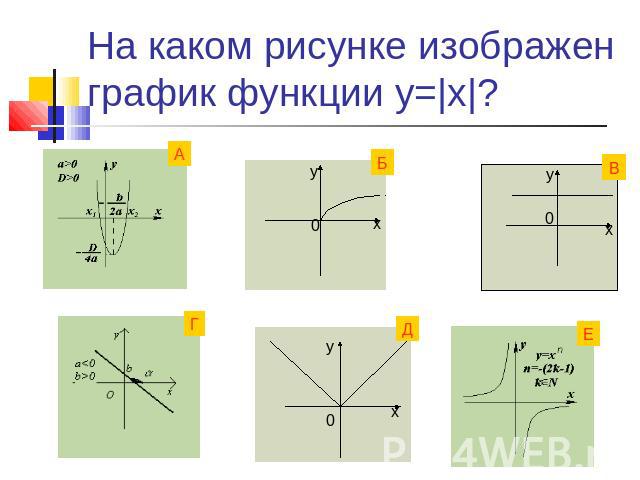
На каком рисунке изображен график функции у=|х|?

Какие из следующих уравнений вы не умеете решать? 1.5х-6=-7х+23 2.|2х-5|=2-х 3.4/х=5-х 4.х² – 5х + 6 = 0 5. 2 х² 3х+2 х-2 2-х

1. Использование определения модуля |0,2х-2|=3,6 Решение. 0,2х-2 = 3,6 или 0,2х-2 = -3,6 0,2х = 3,6+2 0,2х =-3,6+2 0,2х =5,6 0,2х = -1,6 х =28 х =-8 Ответ: -8;28

2. Графический способ

3. Метод введения новой переменной (х+3)²-|4х+12|-21=0 Решение |х+3|²-4|х+3|-21=0 Пусть |х+3|=t, тогда получаем уравнение t²-4t-21=0. t=-3 или t=7.Возвращаемся к переменной х: |х+3|=-3 |х+3|=7 - решений нет, х+3=7 или х+3=-7 х=4 х=-10 Ответ: -10;4.

Домашнее задание № 1133(а, б) № 1140(в),1144(г) |х+2|=2(3-х) х² –|х | =20

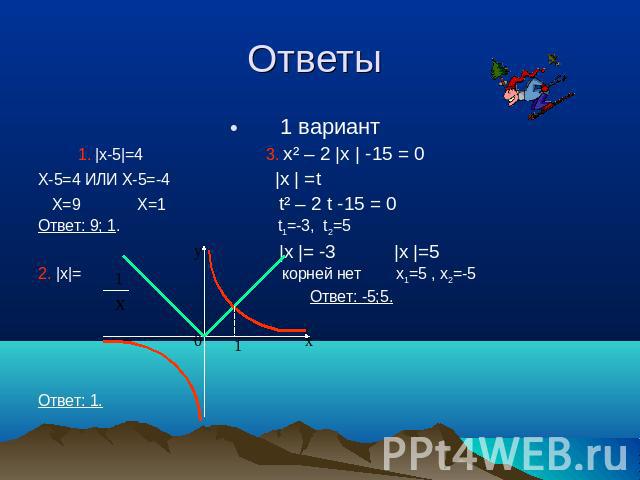
Проверь себя! 1 вариант |х-5|=4 |х|= х² – 2 |х | -15 = 0

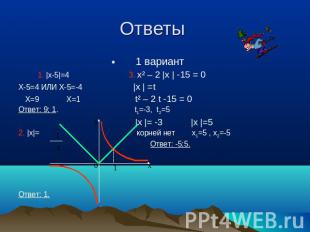
Ответы 1 вариант 1. |х-5|=4 3. х² – 2 |х | -15 = 0 Х-5=4 ИЛИ Х-5=-4 |х | =t Х=9 Х=1 t² – 2 t -15 = 0 Ответ: 9; 1. t1=-3, t2=5 |х |= -3 |х |=5 2. |х|= корней нет х1=5 , х2=-5 Ответ: -5;5. Ответ: 1.

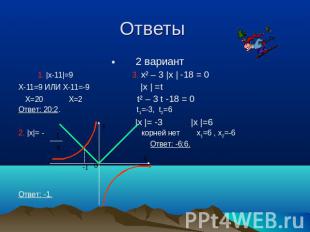
Ответы 2 вариант 1. |х-11|=9 3. х² – 3 |х | -18 = 0 Х-11=9 ИЛИ Х-11=-9 |х | =t Х=20 Х=2 t² – 3 t -18 = 0 Ответ: 20;2. t1=-3, t2=6 |х |= -3 |х |=6 2. |х|= - корней нет х1=6 , х2=-6 Ответ: -6;6. Ответ: -1.

Поставь оценку! «5»-решены верно все уравнения «4»- решены верно два уравнения «3»- решено верно одно уравнение «2»- ни одно уравнение не решено верно

Запомни!

Какое из предложенных уравнений мы не решили? |3х-1|= |2х+3| ? Попробуй решить это уравнение!