Презентация на тему: Решение тригонометрических уравнений, содержащих радикалы

Решение тригонометрических уравнений , содержащих радикалы Курылева С.С., учитель математики МОУ «Лицей №1» г. Воркуты

Эпиграф: Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это путь самый легкий и путь опыта – это путь самый горький. Конфуций

Задачи на урок: совершенствовать навыки решения тригонометрических уравнений различными способами; продолжить формирование умений применять различные способы отбора корней в тригонометрических уравнениях; Развивать познавательный интерес, интеллектуальные способности.

Решение простейших тригонометрических уравнений

Частные случаи записи решения уравнения

Частные случаи записи решения уравнения

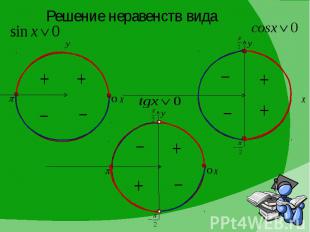
Решение неравенств вида

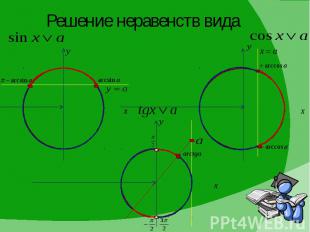
Решение неравенств вида

Решение некоторых иррациональных уравнений

Способы отбора корней в тригонометрических уравнениях

Арифметический способ Данный способ отбора корней связан с вычислением корней при переборе значений целочисленного параметра или нахождением значений тригонометрических выражений непосредственной подстановкой при отборе корней.

Непосредственная подстановка В случае непосредственной подстановки серий полученных решений для удаления «посторонних» решений полезно использование формул приведения. В частности,

Алгебраический способ Применяется если заданные ограничения охватывают большой промежуток, т последовательный перебор значений параметров приводит к громоздким вычислениям; серии решений содержат нетабличные значения обратных тригонометрических функций; требуется определить количество корней уравнения, удовлетворяющих дополнительным условиям.

Тригонометрическая окружность Удобно использовать при отборе корней на промежутке длина которого не превосходит ; в случае, когда значения обратных тригонометрических функций, входящих в серию решений, не являются табличными.

Основные методы решения тригонометрических уравнений: разложение на множители; способ замены; сведение к уравнениям, однородным относительно и ; преобразование суммы тригонометрических функций в произведение; преобразование произведения в тригонометрических функций в сумму; использование формул понижения степени; равенство одноименных тригонометрических функций; введение вспомогательного аргумента.

Тренировочные упражнения Решите уравнения: Уравнение 1 Ответ: Уравнение 2 Ответ: Уравнение 3 Ответ:

Проверь себя Самостоятельная работа

Проверь себя!!!

Спасибо за урок! Удачи на ЕГЭ!!!