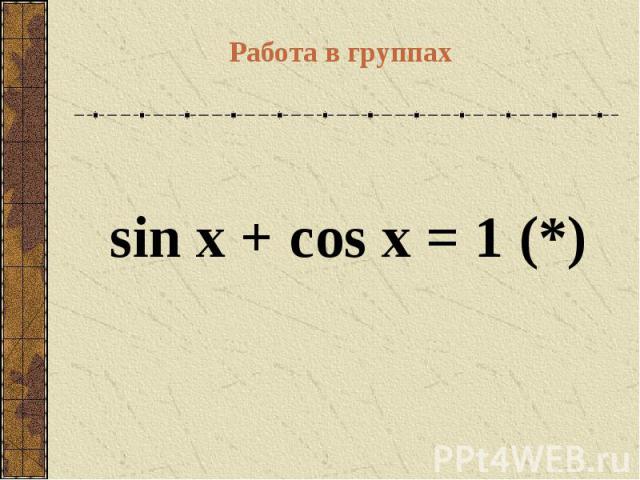Презентация на тему: Урок одной задачи. Решение тригонометрических уравнений разными способами

Урок – практикум по теме: «Урок одной задачи. Решение тригонометрических уравнений разными способами»  Урок – практикум по теме: «Урок одной задачи» РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ РАЗНЫМИ СПОСОБАМИ

План урока SIN α ; COS α1.Организационный момент 2. Повторение материала 3. Работа в группах 4. Тестирование 5. Домашнее задание 6. Итог урока

1. 2 cos² x + 3 cos x + 1 = 0; 2. 3sin x = 2 cos2 x;3. 2 cos2 3x + sin 3x – 1 = 0;4. (sin x – 0,5) (sin x + 1) = 0; 5. tg3 х - tg2 x – 3tg x + 3 = 0;6. tg x – 15/tg x = 2;7. sin 2x cos x + 2 sin3 x = 1;8. cos x + sin x = √2;9. 8 sin x — 6 sin x cos x + 3 cos x – 4 = 0; 10. cos² x = 1; 11. cos² πx + 4 sin πx + 4 = 0; 12. cos (2x - π/4) = -1; 13. 3 sin x + 4 cos x = 2.

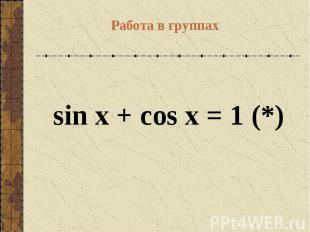
Работа в группах sin x + cos x = 1(*)  

I способ sin x + cos x = 1(*) Введение вспомогательного угла sin x + cos x = 1 | √2

II способsin x + cos x = 1(*) Введение выражений для sin α и сos α через tg по формулам sin α = 2tg α/2 / 1 + tg² α /2 cos α = 1- tg² α /2 / 1 + tg² α /2 (1)

III способsin x + cos x = 1(*) Сведение к одному уравнению Выразим sin x, cos x и 1 через функции половинного аргумента:2 sin x/2 · cos x/2 + cos² x/2 - sin² x/2 = sin² x/2 + cos² x/2

IV способsin x + cos x = 1(*) Преобразование суммы в произведение Выразим cos x через sin (π/2 – x)

V способsin x + cos x = 1(*) Применение формулы sin x + cos x = √2 sin (x + π/4)

VI способsin x + cos x = 1(*) Возведение в квадрат обеих частей уравнения (*) ( sin x + cos x)2 = 1

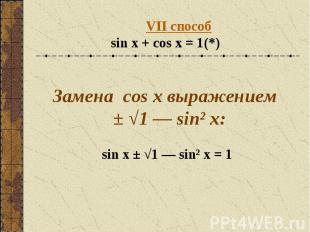
VII способsin x + cos x = 1(*) Замена cos x выражением ± √1 — sin² x:sin x ± √1 — sin² x = 1

Самостоятельная работа I вариант № 1 Решить уравнение: cos 0,5x = - 1 № 2 Решить уравнение: № 3 Решить уравнение: 2 cos2 x = 3 sin x

Ф.И. _______________________________________Нуждаешься ли ты в индивидуальной консультации?Да ______Нет ______Затрудняюсь: А) при решении простейших тригонометрических уравнений: ____Б) при решении однородных тригонометрических уравнений: ____В) при решении тригонометрических уравнений методом разложения на множители: _________ Г) при решении тригонометрических уравнений, приводимых к алгебраическим методом подстановки: _______

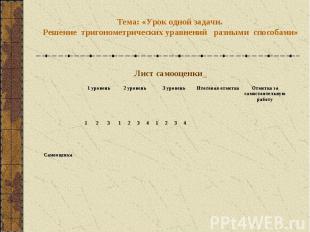
Тема: «Урок одной задачи. Решение тригонометрических уравнений разными способами»Лист самооценки