Презентация на тему: Решение простейших тригонометрических уравнений

Решение простейших тригонометрических уравненийШахова Т. А.МОУ гимназия №3 г. Мурманска.

Чтобы успешно решать простейшие тригонометрическиеуравнения необходимо следующее: ) уметь отмечать точки на числовой окружности;2) уметь определять значения синуса, косинуса, тангенса и котангенса для точек числовой окружности;3) знать свойства основных тригонометрических функций;) знать понятие арксинуса, арккосинуса, арктангенса, арккотангенса и уметь отмечать их на числовой окружности.

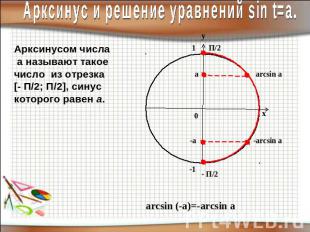
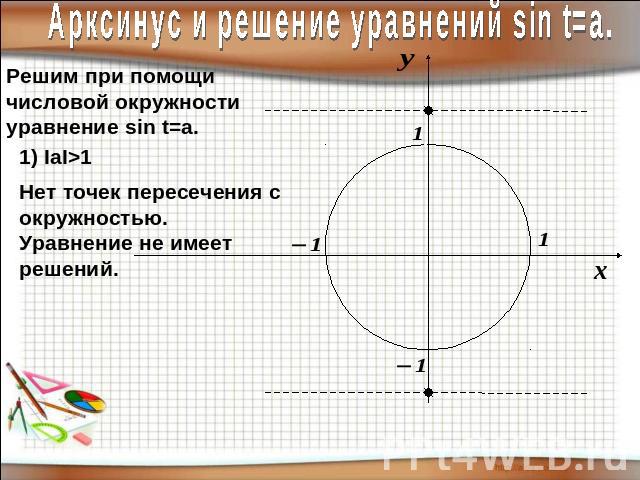
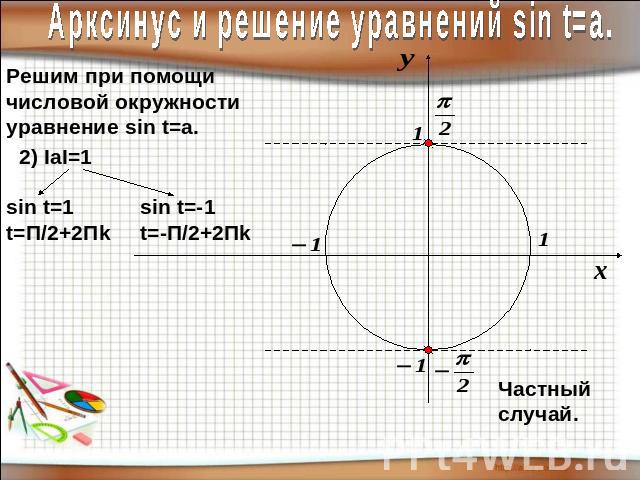
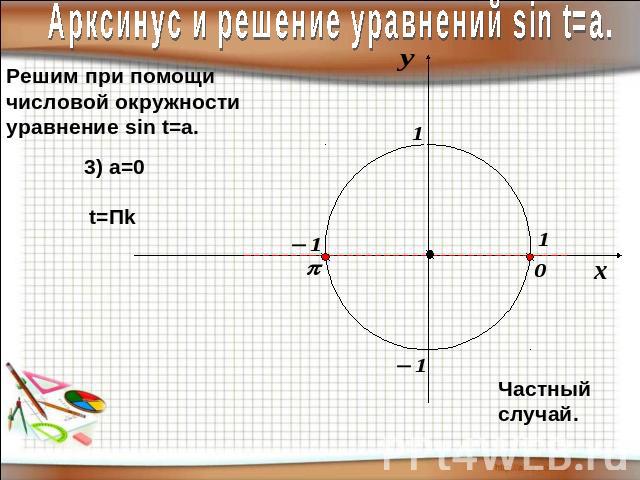
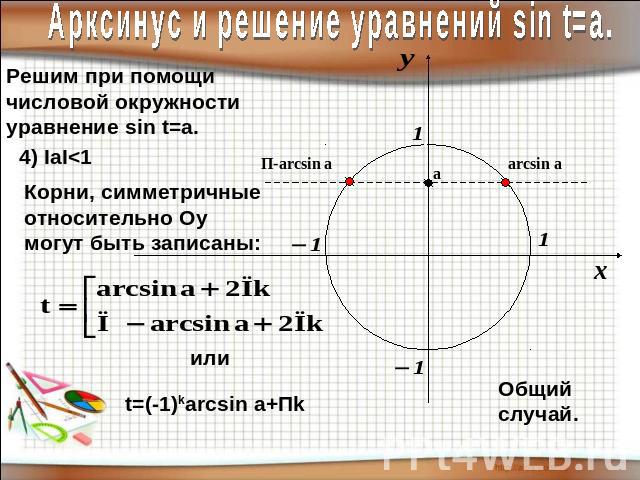
Арксинус и решение уравнений sin t=a.Арксинусом числа а называют такое число из отрезка [- П/2; П/2], синус которого равен а.

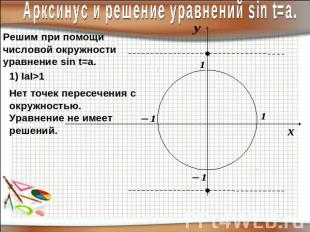
Арксинус и решение уравнений sin t=a.Решим при помощичисловой окружностиуравнение sin t=a.Нет точек пересечения с окружностью.Уравнение не имеет решений.

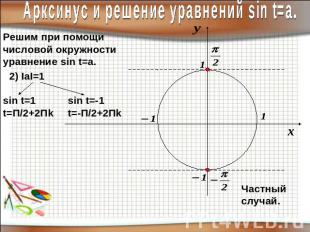
Арксинус и решение уравнений sin t=a.Решим при помощичисловой окружностиуравнение sin t=a.

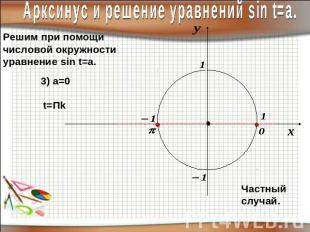
Арксинус и решение уравнений sin t=a.Решим при помощичисловой окружностиуравнение sin t=a.

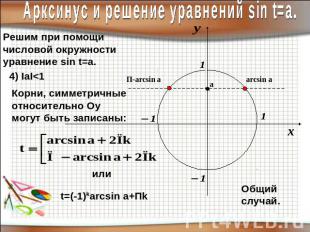
Арксинус и решение уравнений sin t=a.Решим при помощичисловой окружностиуравнение sin t=a.Корни, симметричные относительно Оу могут быть записаны:

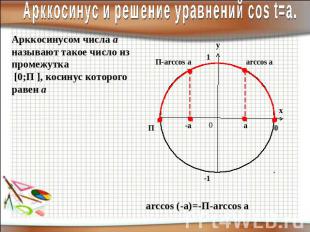
Арккосинус и решение уравнений соs t=a.Арккосинусом числа а называют такое число из промежутка [0;П ], косинус которого равен а

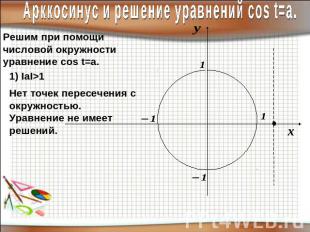
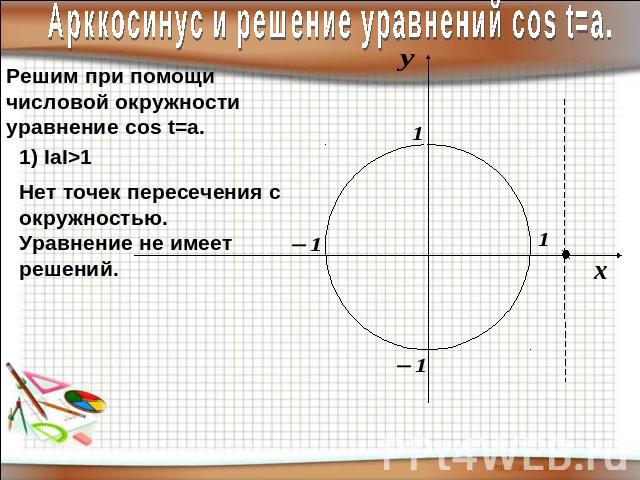
Арккосинус и решение уравнений соs t=a.Решим при помощичисловой окружностиуравнение cos t=a.Нет точек пересечения с окружностью.Уравнение не имеет решений.

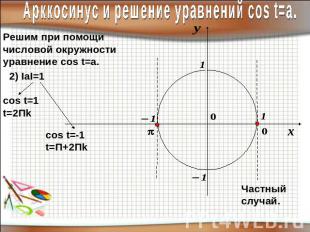
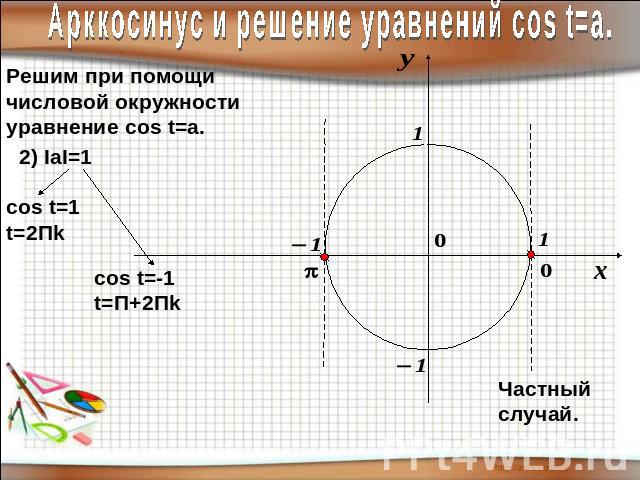
Арккосинус и решение уравнений соs t=a.Решим при помощичисловой окружностиуравнение cos t=a.

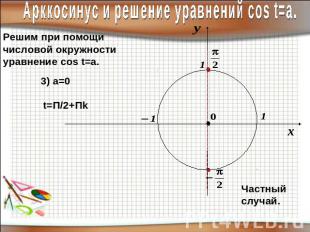
Арккосинус и решение уравнений соs t=a.Решим при помощичисловой окружностиуравнение cos t=a.

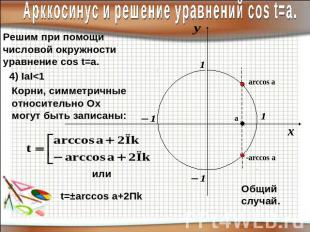
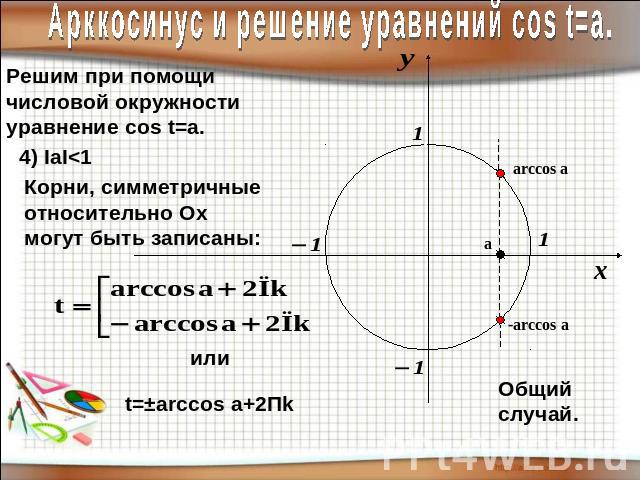
Арккосинус и решение уравнений соs t=a.Решим при помощичисловой окружностиуравнение cos t=a.Корни, симметричные относительно Оx могут быть записаны:

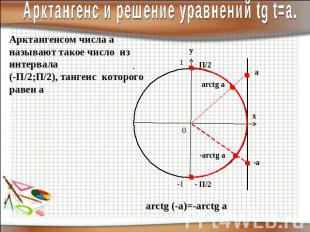
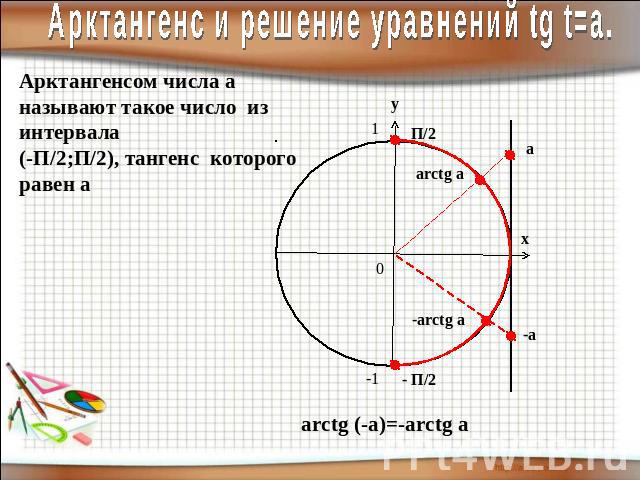
Арктангенс и решение уравнений tg t=a.Арктангенсом числа а называют такое число из интервала (-П/2;П/2), тангенс которого равен а

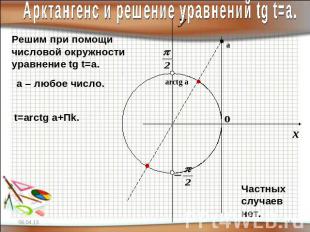
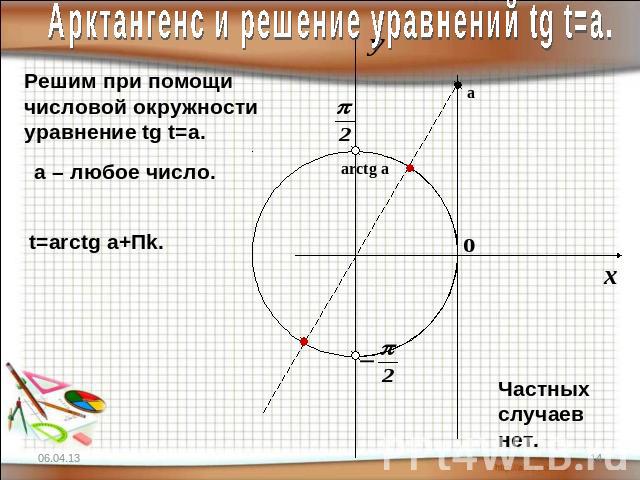
Арктангенс и решение уравнений tg t=a.Решим при помощичисловой окружностиуравнение tg t=a.

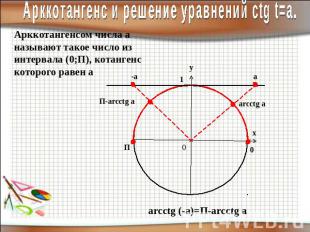
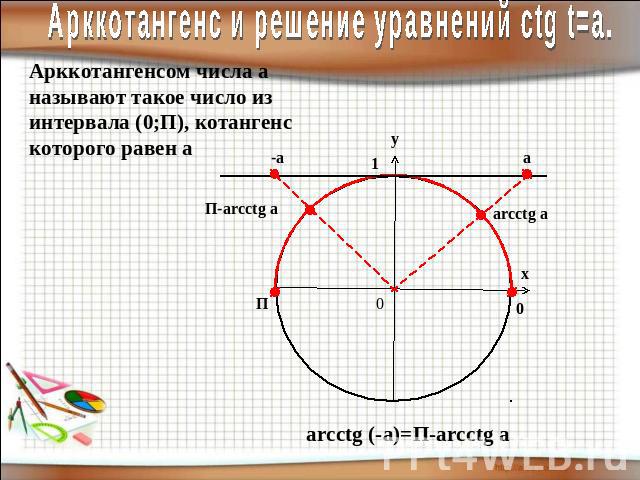
Арккотангенс и решение уравнений сtg t=a.Арккотангенсом числа а называют такое число из интервала (0;П), котангенс которого равен а

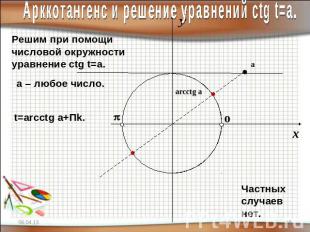
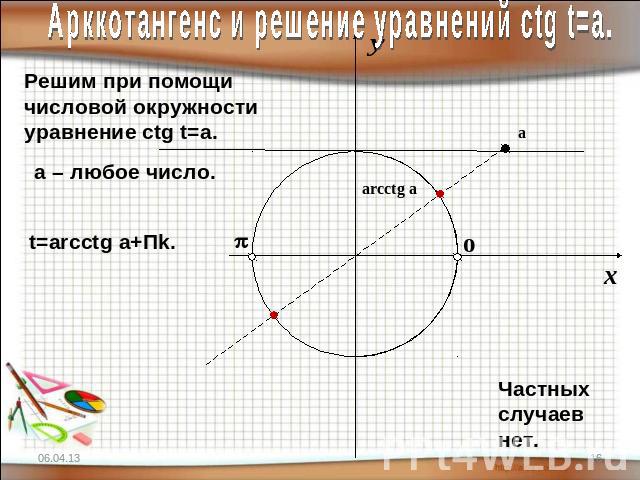
Арккотангенс и решение уравнений сtg t=a.Решим при помощичисловой окружностиуравнение сtg t=a.

Наша задача: свести любое тригонометрическое уравнение к простейшему виду.

Примеры уравнений.Уравнение уже имеет простейший вид , однако можно применить формулы приведения и упростить его.

Характерная ошибкаУчащиеся делят обе части на 4 и получают следующее:

Примеры уравнений.Уравнение переносом слагаемого и делением обеих частей легко сводится к простейшему.

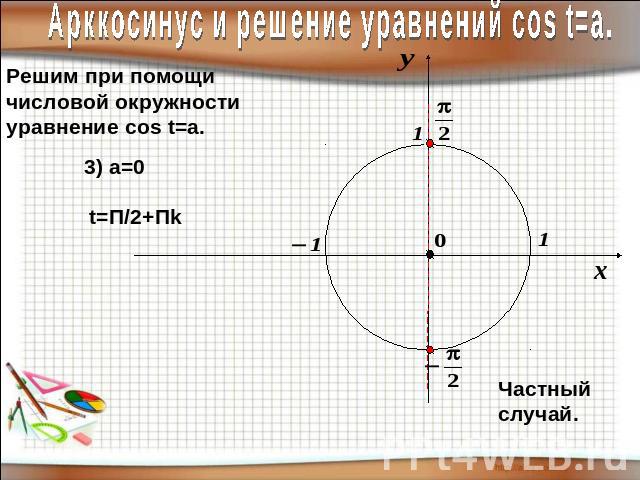
Примеры уравнений.Уравнение уже имеет простейший видЭто частный вид уравнения cos t=a a=0

Примеры уравнений.Уравнение уже имеет простейший вид , однако, можно использовать четность функции cos, применить формулы приведения и упростить его.

Примеры уравнений.Здесь уместно использовать формулу косинуса разности аргументов:Теперь уравнение имеет простейший вид.Решение удобнее разбить на два.

Потренируйся.

Спасибо за то, что стараешься!