Презентация на тему: Решение простейших тригонометрических неравенств

Решение простейших тригонометрических неравенств

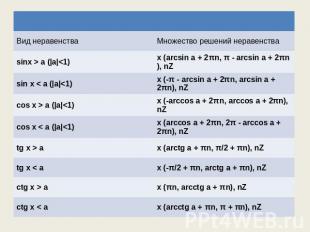
Решение неравенств, содержащих тригонометрические функции обычно сводится к решению простейших неравенств вида: sin(t)<(≤;>;≥)a; cos(t)<(≤;>;≥)a; tg(t)<(≤;>;≥)a; ctg(t)<(≤;>;≥)a; Способы решения этих неравенств совершенно очевидным образом вытекают из представления тригонометрических функций на единичном круге.
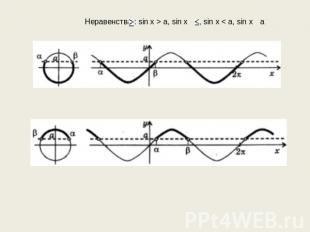


Тригонометрическое неравенство sin(t)≥a. Все точки Pt единичной окружности при значениях t, удовлетворяющих данному неравенству, имеют ординату, большую или равную -1/2. Множество таких точек это дуга l, которая выделена жирным на рисунке ниже. Найдем условие принадлежности точки Pt этой дуге. Точка Pt лежит на правой полуокружности, ордината Pt равна 1/2, и, следовательно, в качестве t1 удобно взять значение t1=arcsin(-1/2)=-π/6. Представим себе, что мы совершаем обход дуги l от точки Pt1 к Pt2 против часовой стрелки. Тогда t2 > t1, и, как легко понять, t2=π-arcsin(-1/2)=7*π/6. Таким образом, получаем, что точка Pt принадлежит дуге l, если -π/6 ≤ t ≤ 7*π/6. Таким образом, решения неравенства, принадлежащие промежутку [-π/2 ; 3*π/2] длиной 2*π таковы: -π/6 ≤ t ≤ 7*π/6. Вследствие периодичности синуса остальные решения получаются добавлением к найденным чисел вида 2πn, где n - целое. Таким образом, мы приходим к ответу: -π/6+2πn≤t≤7π/6+2πn, n - целое.

Пример 1 Решите неравенство Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит Для x [0; 2π] решением данного неравенства будут Ясно также, что если некоторое число x будет отличаться от какого-нибудь числа из указанного интервала на 2π n то sin x также будет не меньше Следовательно, к концам найденного отрезка решения нужно просто добавить 2π n , где Окончательно, получаем, что решениями исходного неравенства будут все где Ответ. где
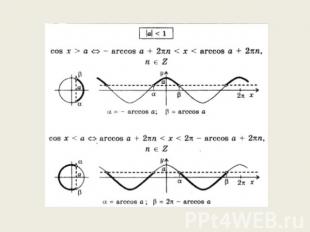


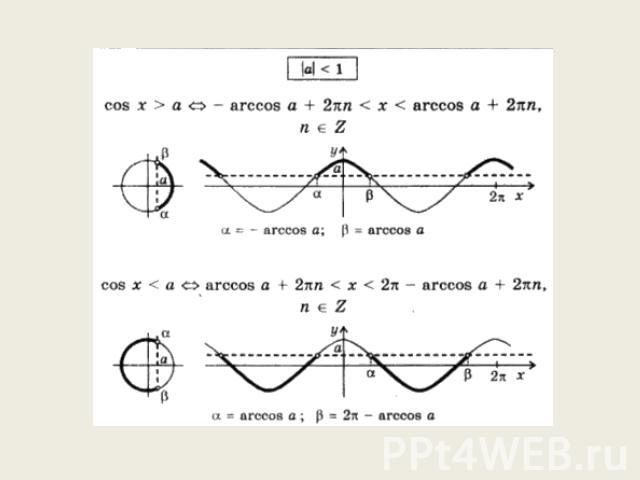
Тригонометрическое неравенство cos(t)<a Рассмотрим решение простейших тригонометрических неравенств с косинусом на примере решения неравенства cos(t)<1/2. Множество точек единичной окружности, абсциссы которых меньше 1/2 левее прямой x=1/2. Значит, множкество всех таких точек есть дуга l, выделенная на рисунке ниже жирным, прияем ее концы Pt1 и Pt2 не входят в это множкество. Необходимо найти точки t1 и t2. Точка Pt1 расположена на верхней полуокружности, абсцисса Pt1 равна 1/2, следовательно t1=arccos(1/2)=5*π/3. При переходе от точки Pt1 к Pt2 по дуге l выполняем обход против движения часовой стрелки, тогда t2>t1 и t2=2π-arccos(1/2)=5π/3. Точка принадлежит выделенной дуге l (исключая ее концы) при условии, что π/3<t<5π/3. Решения неравенства, принадлежащие промежутку [0; 2π] длиной 2π, таковы: π/3<t<5π/3. Вследствие периодичности косинуса остальные решения получаются добавлением к найденным чисел вида 2πn, где n - целое. Таким образом, мы приходим к окончательному ответу: π/3+2πn<t<5π/3+2πn, n - целое.
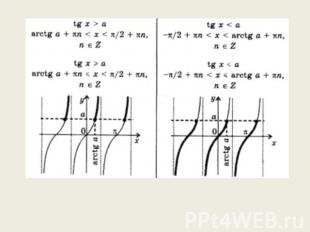

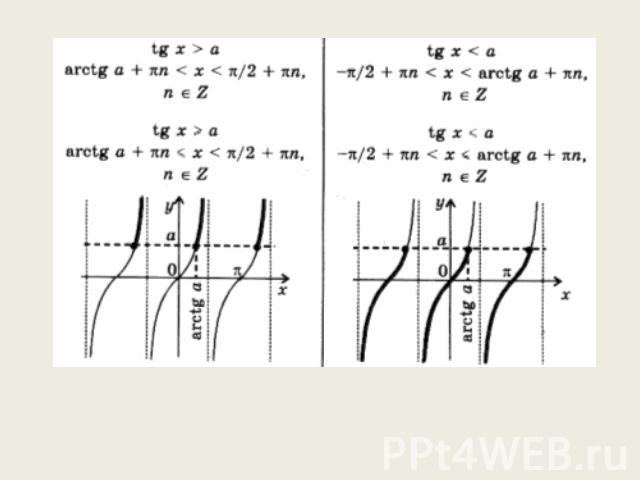
Тригонометрическое неравенство tg(t)≤a Рассмотрим способ решения тригонометрического неравенства с тангенсом на примере неравенства tg(t)≤1. период тангенса равен π Найдем сначала все решения данного неравенства, принадлежащие промежутку (-π/2; π/2), а затем воспользуемся периодичностью тангенса. Для выделения всех точек Pt правой полуокружности, значения t которых удовлетворяют данному неравенству, обратимся к линии тангенсов. Если t является решением неравенства, то ордината точки T - луч AT (см. рисунок ниже). Множество точек Pt, соответствующих точкам этого луча, - дуга l, выделенная на рисунке жирным. Следует отметить, что точка Pt1 принадлежит рассматриваемому множеству, а Pt2 нет. Найдем условие, при котором точка Pt принадлежит дуге l. t1 принадлежит интервалу (-π/2 ; π/2), и tf(t)=1, следовательно t1=arctg(1)=π/4. Значит t должно удовлетворять условию -π/2<t≤π/4. Все решения данного неравенства, принадлежащие промежутку (-π/2 ; π/2), таковы: (-π/2 ; π/4]. учитывая периодичность тангенса, приходим к окончательному ответу: -π/2+πn<t≤π/4+πn, n - целое.

Сабитова Файруза Рифовна преподаватель математики ГАОУ СПО «Сармановский аграрный колледж»




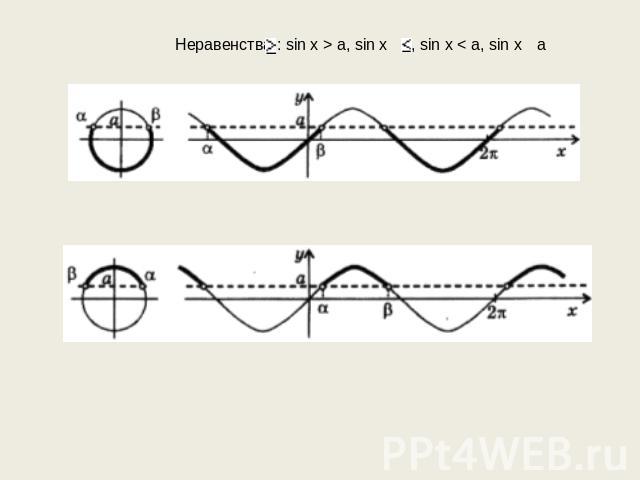


![Пример 1 Решите неравенство Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит Для x [0; 2π] решением данного неравенства будут Ясно также, что если некоторое число x будет отличаться от какого-нибудь… Пример 1 Решите неравенство Нарисуем тригонометрическую окружность и отметим на ней точки, для которых ордината превосходит Для x [0; 2π] решением данного неравенства будут Ясно также, что если некоторое число x будет отличаться от какого-нибудь…](/images/288/15492/640/img6.jpg)