Презентация на тему: Площадь треугольника

Площадь треугольника

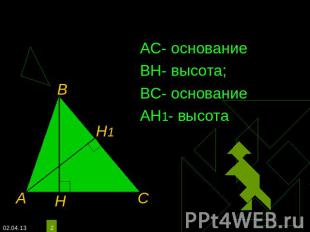
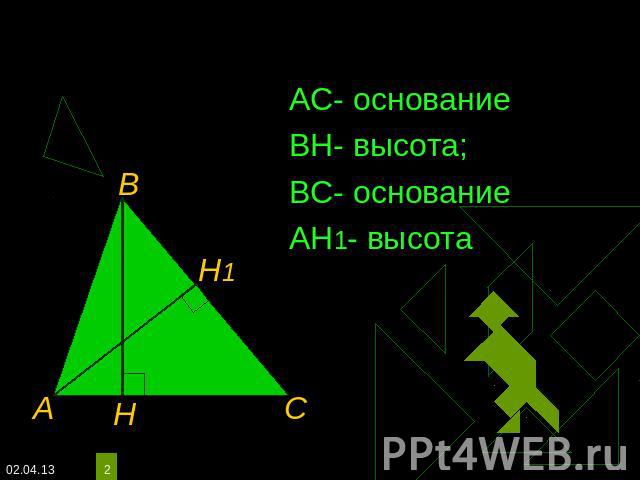
АС- основаниеВН- высота;ВС- основаниеАН1- высота

Теорема. Площадь треугольника равна половине произведения его основания на высоту. Дано: АВС; СН- высота; АВ- основание.Док-ть: S= ½ АВ СН.Док-во: АВС= DСВ (по трем сторонам (СВ- общая, АВ= СД, АС= ВД )) SАВС =SDСВ SАВС= ½ S ABCD, т.е. S = = ½ АВ СН. Теорема доказана.

Следствие 1. Площадь прямоугольного треугольника равна половине произведения его катетов. ВС- гипотенуза;АВ и АС- катеты. АВС- прямоугольный;SАВС= ½ АВ АС.

Следствие 2. Если высоты двух треугольников равны, то их площади относятся как основания.ВН= В1Н1S/S1= АС/А1С1

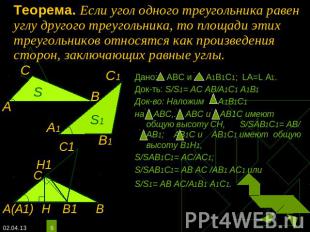
Теорема. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы. Дано: АВС и А1В1С1; LА=L А1.Док-ть: S/S1= АС АВ/А1С1 А1В1Док-во: Наложим А1В1С1на АВС,. АВС и АВ1С имеют общую высоту СН, S/SАВ1С1= АВ/ АВ1; АВ1С и АВ1С1 имеют общую высоту В1Н1, S/SАВ1С1= АС/АС1; S/SАВ1С1= АВ АС /АВ1 АС1 или S/S1= АВ АС/А1В1 А1С1.