Презентация на тему: Золотая теорема геометрии

Золотая теорема геометрии Различные доказательства теоремы Пифагора8 классМОУ “Яконурская средняя общеобразовательная школа”Учитель математики Елекова Эльвира Михайловна

Золотая теорема геометрии Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов.

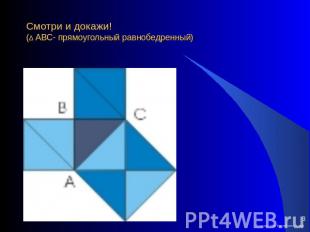
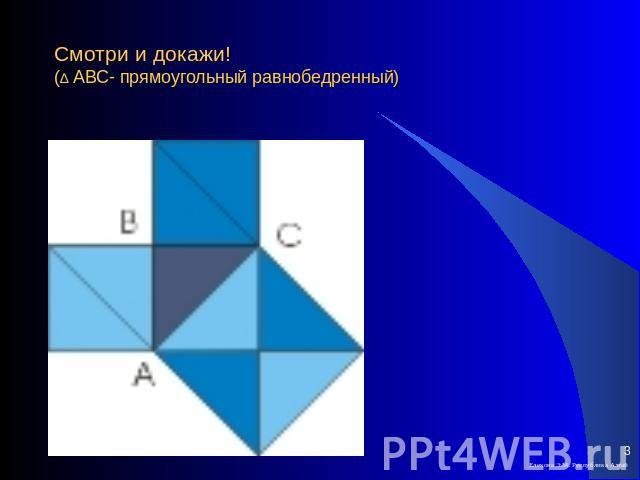
Смотри и докажи!(∆ АВС- прямоугольный равнобедренный)

Смотри и докажи!

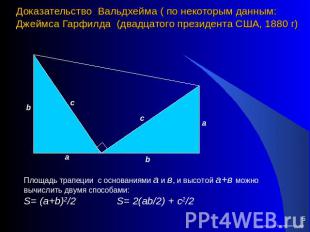
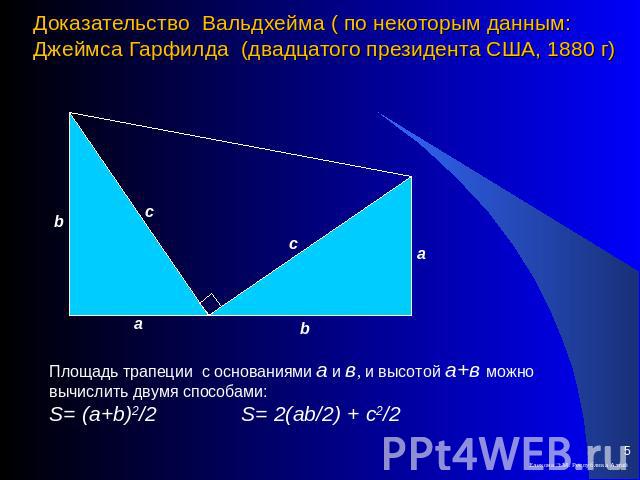
Доказательство Вальдхейма ( по некоторым данным: Джеймса Гарфилда (двадцатого президента США, 1880 г) Площадь трапеции с основаниями а и в, и высотой а+в можно вычислить двумя способами:S= (a+b)2/2 S= 2(ab/2) + c2/2

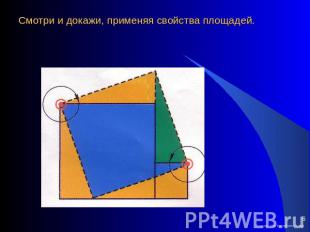
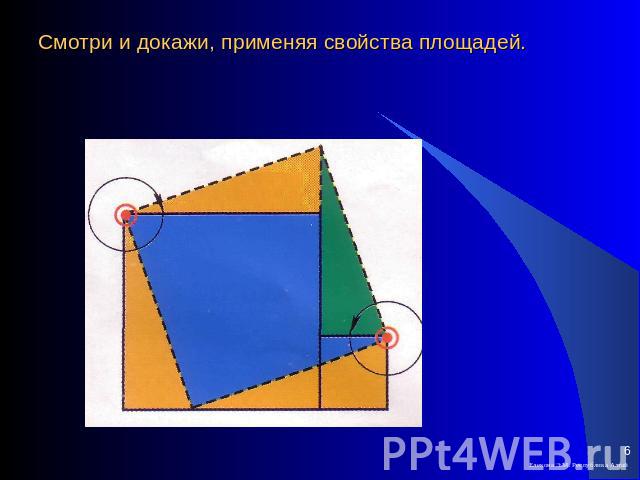
Смотри и докажи, применяя свойства площадей.

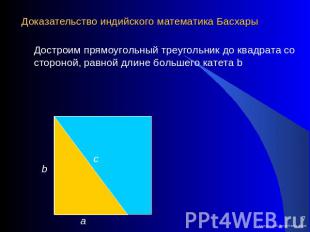
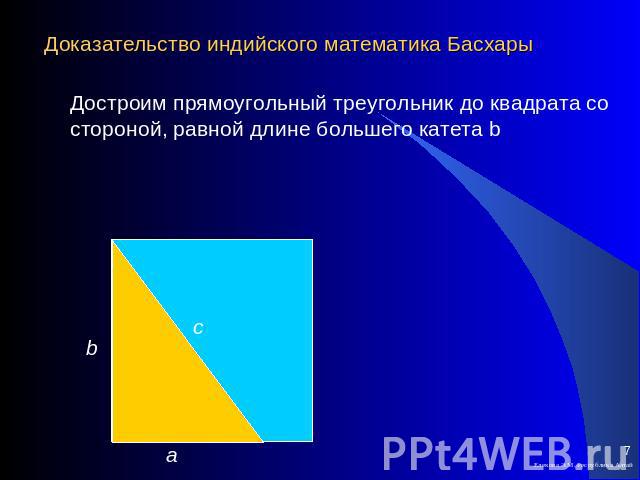
Доказательство индийского математика Басхары Достроим прямоугольный треугольник до квадрата со стороной, равной длине большего катета b

Отложим точно такие же треугольники как показано на рисунке.

На рисунке есть квадрат, площадь которого равна b2Есть квадрат, площадь которого равна c2

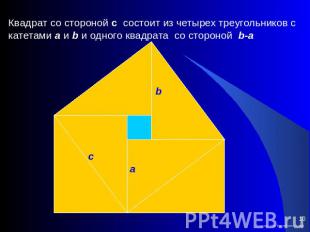
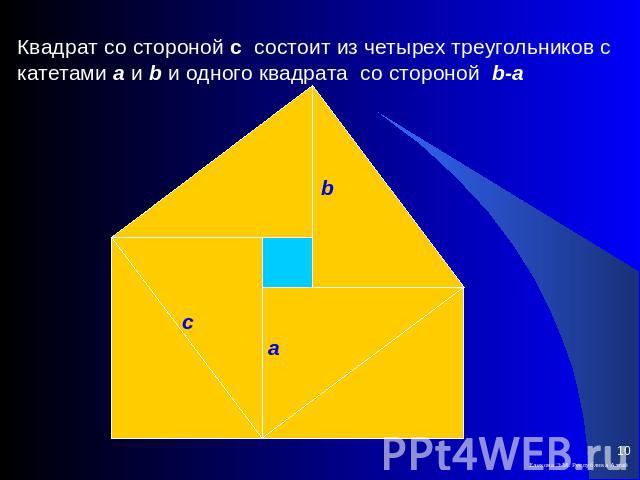
Квадрат со стороной с состоит из четырех треугольников с катетами a и b и одного квадрата со стороной b-a

Рассуждения: Большой квадрат состоит из четырех равных прямоугольных треугольников с катетами а и b и одного квадрата со стороной b-a т.е. с2=4∙Sтр + (b-a)2== 4∙(ab/2) + (b-a)2= 2ab + b2 - 2ab + a2 == a2 + b2 Итак, с2 = a2 + b2 что и требовалось доказать.

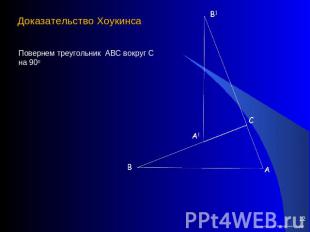
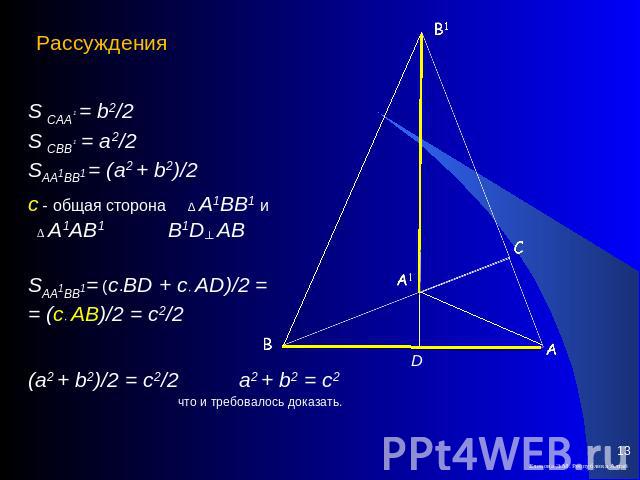
Доказательство Хоукинса Повернем треугольник АВС вокруг С на 900

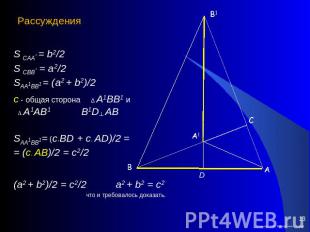
Рассуждения S САА1 = b2/2S СВВ1 = a2/2SAA1BB1 = (a2 + b2)/2с - общая сторона ∆ А1ВВ1 и ∆ А1АВ1 B1D┴ ABSAA1BB1= (c∙BD + c∙ AD)/2 = = (c∙ AB)/2 = c2/2

Образовательные ресурсы Теорема Пифагора - история, доказательства, применения. http://th-pif.narod.ru/index.htm Сайт учителя Шапошникова И.М. Геометрия. http://moypifagor.narod.ru Теорема Пифагора. http://th-pif.narod.ru/formul.htmВ. Литцман Теорема Пифагора. http://ega-ath.narod.ru/Books/Pythagor.htm