Презентация на тему: Соотношения между сторонами и углами прямоугольного треугольника

Соотношения между сторонами и углами прямоугольного треугольника Составила учитель математики МОУ СОШ №127 г.Перми: Коблова С.Ю.

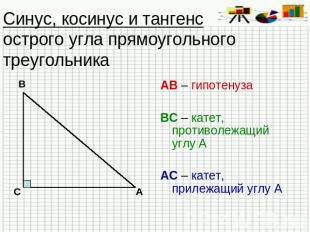
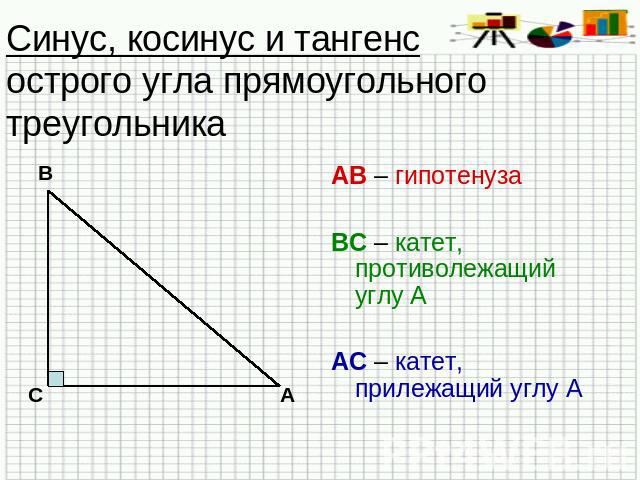
Синус, косинус и тангенс острого угла прямоугольного треугольника АВ – гипотенузаВС – катет, противолежащий углу ААС – катет, прилежащий углу А

Синус, косинус и тангенс острого угла прямоугольного треугольника Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Синус, косинус и тангенс острого угла прямоугольного треугольника Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Синус, косинус и тангенс острого угла прямоугольного треугольника Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Тригонометрические тождества Основное тригонометрическое тождество:Приведите доказательство (учебник, п.66)2) Тангенс угла равен отношению синуса к косинусу этого угла.Приведите доказательство (учебник, п.66)

Значения синуса, косинуса и тангенса угла 30° . Рассмотрим прямоугольный треугольник АВС:ﮮА=30°, ﮮВ=60° Так как катет, лежащий против угла 30°, равен половине гипотенузы, то Но Значит, Из основного тригонометрического тождества получаем По 2-му тождеству находим

Значения синуса, косинуса и тангенса угла 60°. Рассмотрим прямоугольный треугольник АВС:ﮮА=30°, ﮮВ=60° Так как катет, лежащий против угла 30°, равен половине гипотенузы, то Или Значит, Из основного тригонометрического тождества получаем По 2-му тождеству находим

Значения синуса, косинуса и тангенса угла 45°. Рассмотрим равнобедренный прямоугольный треугольник АВС: АС=ВС,ﮮА=45°, ﮮВ=45° По теореме Пифагора АВ2= АС2+ ВС2 = 2 АС2 = 2 ВС2, откуда Следовательно,

Таблица значенийдля углов, равных 300, 450, 600. Заполните таблицу (учебник, п.67)