Презентация на тему: Расстояние между скрещивающимися прямыми

Семинар-практикум Расстояние между скрещивающимися прямымиЗубарева Т.В., учитель математикиТемниковской СОШ №1

Цели: Систематизация и обобщение приемов работы с пространственными объектами: прямыми , плоскостями и теламиЗнакомство с новым понятием: расстояние между скрещивающимися прямымиУсвоение и отработка общих приемов определения расстояний между скрещивающимися прямыми

Задачи: Устная работа по актуализация необходимых известных приемов работы с пространственными объектами: прямыми и плоскостямиОпределение нового понятия: расстояние между скрещивающимися прямымиРешение типовых задач на определение расстояний между скрещивающимися прямымиРешение проблемной задачи на обобщение приема нахождения расстояния между скрещивающимися прямыми

Средства: Модели пространственных фигур, чертежи к задачамТеорема Фалеса и теорема о трех перпендикулярах Приемы стерео и планиметрических построенийТиповые и проблемные задачиКомпьютер с мультимедийным проектором

План: Первый урок: Актуализация: выполнение устных заданий, доказательство теоремы, решение задачи Определение и усвоение нового понятия Второй урок . Решение типовых задач на усвоение и отработку нового понятияТретий урок. Проблемная задача на обобщение приема нахождения расстояния между двумя скрещивающимися прямыми

Первый урок Подготовительные устные задачи Параллельны ли прямая B1K и плоскость DD1C1C?Параллельны ли прямые C1D и B1K?Параллельны ли прямая AC и плоскость A1B1C1D1?Параллельны ли прямая AL и плоскость A1B1C1D1?

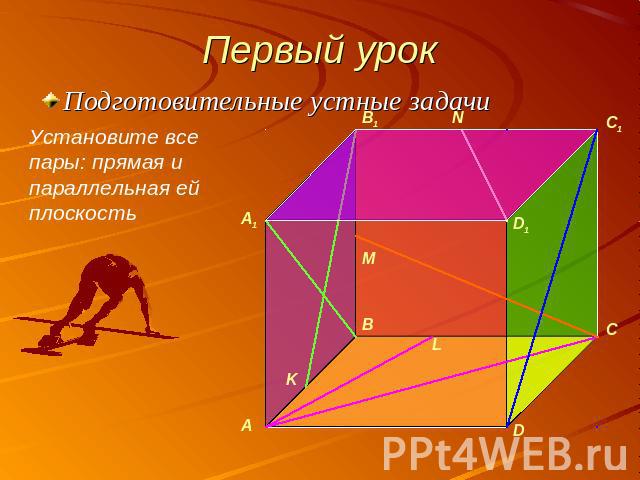
Первый урок Подготовительные устные задачиУстановите все пары: прямая и параллельная ей плоскость

Первый урок Подготовительные устные задачиКак определяется расстояние между прямой и параллельной ей плоскостью?Найдите расстояние между прямой MN и плоскостью AA1D1DНайдите расстояние между прямой MN и плоскостью DD1C1CНайдите расстояние между прямой B1K и плоскостью DD1C1C

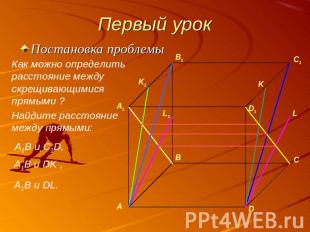
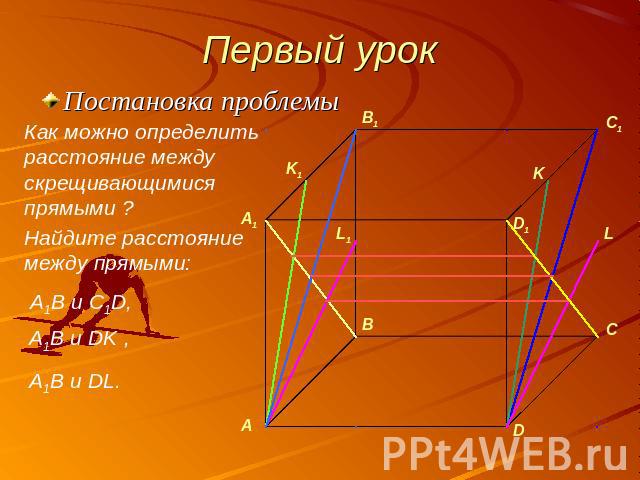
Первый урок Постановка проблемыКак можно определить расстояние между скрещивающимися прямыми ?Найдите расстояние между прямыми: A1B и C1D, A1B и DK ,A1B и DL.

Первый урок Какие следствия можно сформулировать?Отрезок с концами на двух скрещивающихся прямых одновременно перпендикулярный им и есть расстояние между этими прямымиЭтот отрезок равен расстоянию от одной из скрещивающихся прямых до параллельной ей плоскости в которой лежит другая прямая

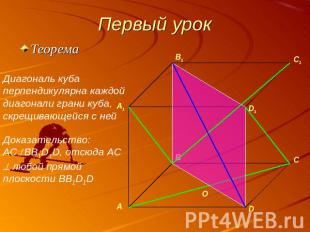
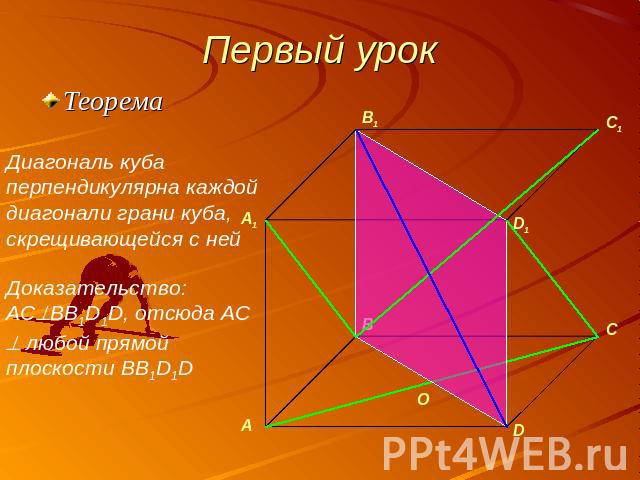
Первый урок ТеоремаДиагональ куба перпендикулярна каждой диагонали грани куба, скрещивающейся с нейДоказательство: ACBB1D1D, отсюда AC любой прямой плоскости BB1D1D

Первый урок Следствие теоремы. Задача.Найдите расстояние между скрещивающимися диагональю куба и диагональю его грани. Решение. Треугольник BB1D перпендикулярен AC. Отрезок OM B1D, будет перпендикулярен и AC . OM - расстояние между AC и B1D.Рассмотрим треугольники BB1D и OMD. Из их подобия следует OM/BB1=OD/B1D

Второй урок Обобщение.Три типовых случая определения расстояния между скрещивающимися прямымиОбщий перпендикуляр к обеим прямым (единственный!)Перпендикуляр от одной из прямых до параллельной плоскости, в которой расположена другая прямая, конец которого не обязательно лежит на прямой!Перпендикуляр между параллельными плоскостями в которых лежат скрещивающиеся прямые, концы которого не обязательно лежат на прямых!

Второй урок Проблема: Как найти плоскость с одной прямой, параллельную другой скрещивающейся прямой ? Достаточно провести через одну из скрещивающихся прямых прямую линию, параллельную другой скрещивающейсяЗаметим, что отрезок соединяющий точки пересечения пар параллельных прямых не равен расстоянию между скрещивающимися прямыми!

Второй урок Типовые задачиЧаще других возникают задачи с перпендикулярными скрещивающимися прямыми. К этому типу относится уже рассмотренная задача о расстоянии между диагональю куба и скрещивающейся диагональю его грани.Стандартный прием решения этих задач заключается в проведении плоскости, в которой лежит одна прямая, перпендикулярно другой скрещивающейся прямой

Второй урок Решение задачДан куб ABCDA1B1C1D1 с длиной ребра AB=a. Найдите расстояние между прямыми AD и D1 M, где M – середина ребра DCПлоскость грани DD1C1C перпендикулярна ребру AD. Из точки D опустим перпендикуляр DK на D1 M. Треугольники DD1M и DKM подобны с коэффициентом подобия 1/2. DK=D1M/2=a√5/2

Второй урок Решение задач Дан куб ABCDA1B1C1D1 с длиной ребра AB=a. Найдите расстояние между прямыми BD и O1 M, где M – середина AO, O и O1 – центры граней ABCD и A1B1C1D1, соответственноДиагональная плоскость AA1C1C перпендикулярна прямой BD. Из точки O опустим перпендикуляр OK на O1 M. Треугольники OO1M и OKM подобны. OK=OO1OM/O1M =a/3 (по теореме Пифагора O1M=3/2√2, OM=1/2√2)

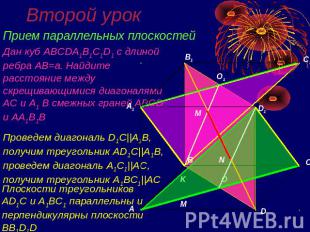
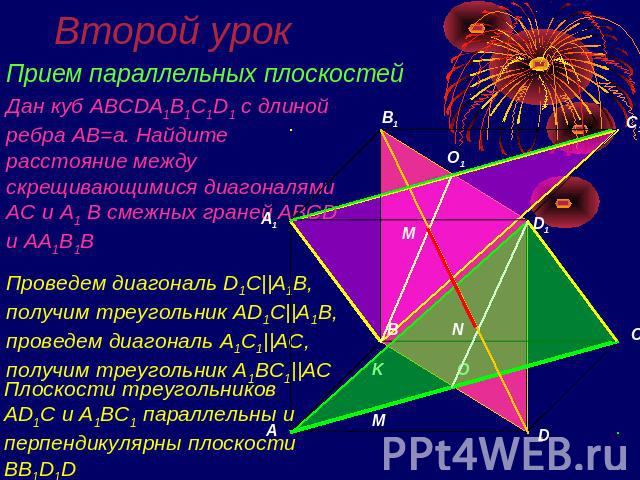
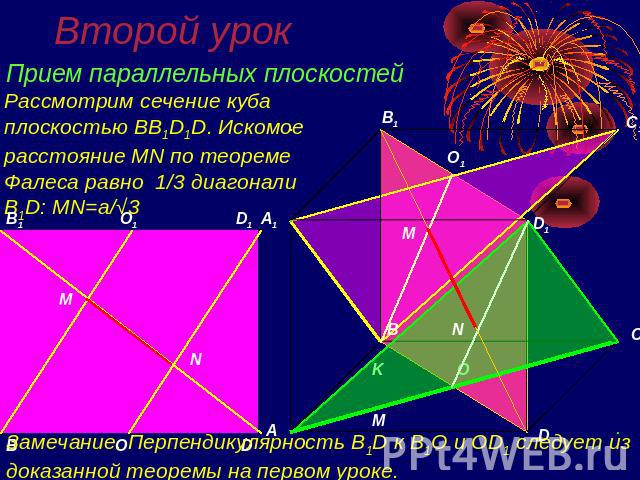
Второй урок Прием параллельных плоскостейДан куб ABCDA1B1C1D1 с длиной ребра AB=a. Найдите расстояние между скрещивающимися диагоналями AC и A1 B смежных граней ABCD и AA1B1BПроведем диагональ D1C||A1B, получим треугольник AD1C||A1B, проведем диагональ A1C1||AC, получим треугольник A1BC1||AC

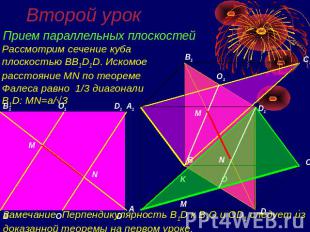
Второй урок Прием параллельных плоскостейРассмотрим сечение куба плоскостью BB1D1D. Искомое расстояние MN по теореме Фалеса равно 1/3 диагонали B1D: MN=a/√3Замечание. Перпендикулярность B1D к B1O и OD1 следует из доказанной теоремы на первом уроке.

Третий урок Обобщение приемов определения расстояний между скрещивающимися прямым Проблема. Даже в случае, если определены параллельные плоскости, в которых лежат прямые, часто трудно найти расстояние между ними –необходимо еще провести третью перпендикулярную плоскостьДля решения проблемы достаточно провести эту плоскость перпендикулярно к одной из прямых!

Третий урок Задача на обобщение приема Проведем через точку A прямую параллельную BM. Из точки B опустим на неё перпендикуляр BK.По теореме о трех перпендикулярах DK AK и треугольник DBK треугольнику ADK , в которой лежит прямая AD.Прямая BM находится на расстоянии BN от плоскости ADK, равном длине перпендикуляра BN к DK!

Третий урок Задача на обобщение приема Вычислим длину отрезка BN через площадь DBK и длину DK. SDBK =a2/4, DK=√5∙a/2, BN=2 SDBK /DK BN=a/ √5

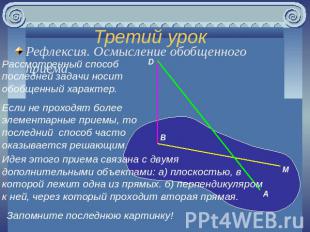
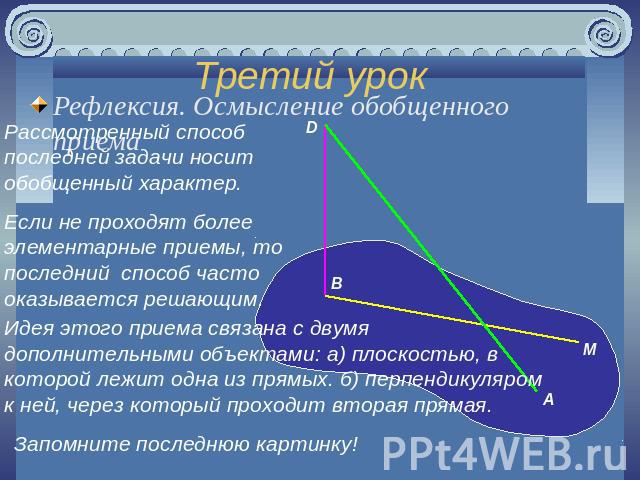
Третий урок Рефлексия. Осмысление обобщенного приема Рассмотренный способ последней задачи носит обобщенный характер.Если не проходят более элементарные приемы, то последний способ часто оказывается решающим.Идея этого приема связана с двумя дополнительными объектами: а) плоскостью, в которой лежит одна из прямых. б) перпендикуляром к ней, через который проходит вторая прямая.

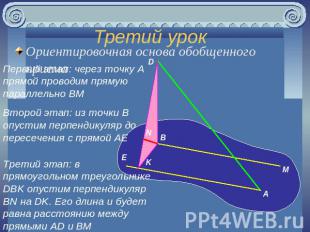
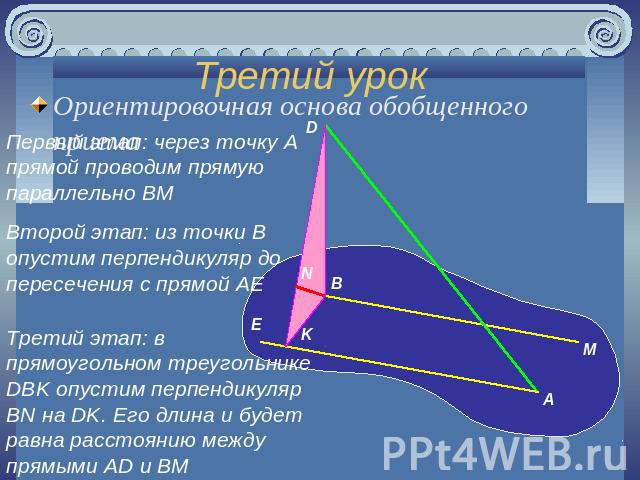
Третий урок Ориентировочная основа обобщенного приема Первый этап: через точку A прямой проводим прямую параллельно BMВторой этап: из точки B опустим перпендикуляр до пересечения с прямой AEТретий этап: в прямоугольном треугольнике DBK опустим перпендикуляр BN на DK. Его длина и будет равна расстоянию между прямыми AD и BM

Третий урок Как найти точки на скрещивающихся прямых AD и BM, ближайшие друг к другу? Через точку N проводим прямую параллельно BM до пересечения с прямой AD в точке L (в плоскости треугольника ADK).Прямоугольный треугольник DBK переносим параллельно вдоль прямой на отрезок NL. Новые положения точек B и N будут ближайшими друг к другу точками прямых AD и BM

Третий урок Задача на закрепление обобщеннного способаВ кубе с длиной ребра a=5 на ребрах AD и D1C взяты точки K и M, соответственно. Найдите расстояние между прямыми A1K и D1M, если AK=4 и DM=3.Решение. Через точку E пересечения A1K c D1D проведем прямую || D1M. Из точки D1 на неё опустим перпендикуляр до пересечения в точке F. Высота D1N треугольника A1D1F и дает искомое расстояние.

Третий урок Решение задачи на закреплениеВычисления. D1H=DMD1E/D1D=35/4=15/4. EH2=A1D12+D1F2=2527/4. EH=45√3/2. SHD1E=225/8. D1F=2SHD1E/EH=5/√3. A1F2=AD12+D1F2=25+25/3. A1F=10/√3. SA1D1F=25/(2√3). D1N=2SH1D1F/A1F=25/10=5/2. Оценка ответа на смысл. D1N=2,5 <DM=3. Проверим путем параллельного переноса D1N до пересечения с A1K.