Презентация на тему: Расстояние между скрещивающимися прямыми. Урок объяснения нового материала

Автор Селезнева С. Н. Расстояние между скрещивающимися прямыми Урок объяснения нового материала Автор Селезнева С. Н.

Определение Отрезок, концы которого лежат на скрещивающихся прямых, и перпендикулярный обеим прямым, называется общим перпендикуляром к скрещивающимся прямым.

Теорема К любым двум скрещивающимся прямым можно провести общий перпендикуляр и притом только один.

Доказательство: а в α β γ А В Значит АВ – общий перпендикуляр

Доказательство единственности а в α β γ А В Допустим, что А1В1 – другой общий перпендикуляр, тогда Значит прямые АВ и А1В1 лежат в одной плоскости. Значит прямые a и b лежат в одной плоскости, что противоречит условию. B1 A1

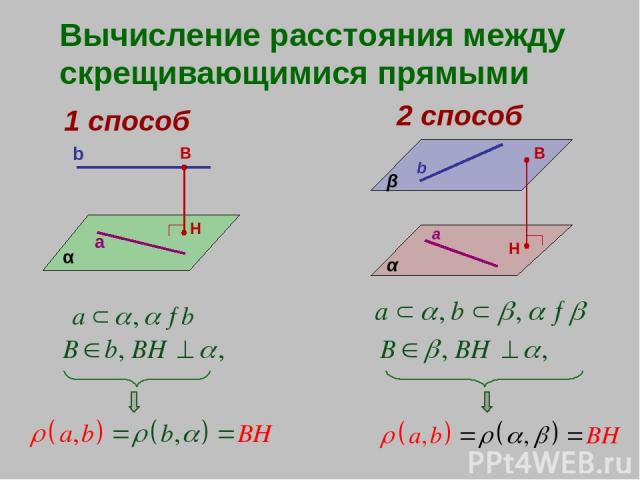
Вычисление расстояния между скрещивающимися прямыми 1 способ α a b B H 2 способ α β b a B H
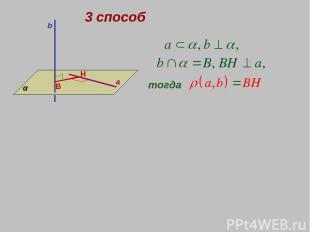
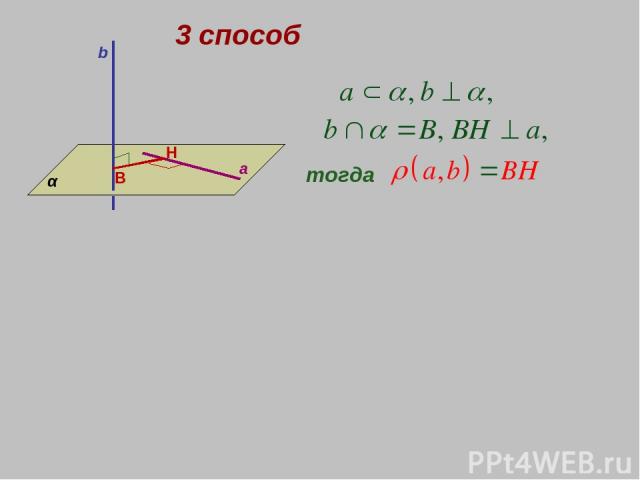
3 способ b a α B H тогда
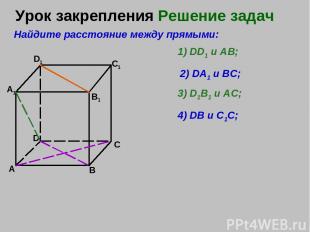
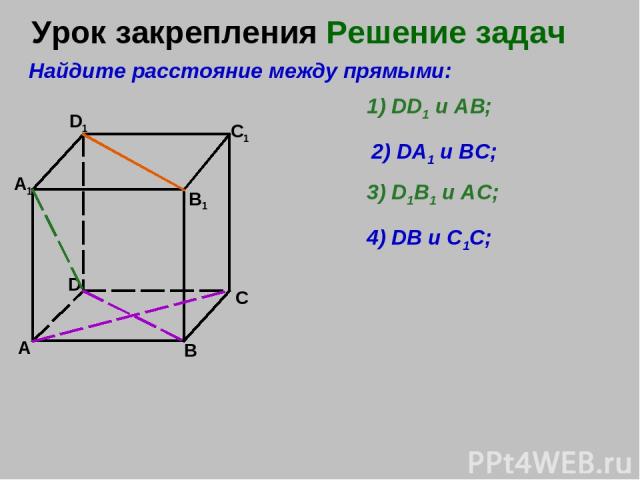
Урок закрепления Решение задач А В C D A1 D1 C1 B1 Найдите расстояние между прямыми: 1) DD1 и АВ; 2) DA1 и ВС; 3) D1B1 и АС; 4) DB и С1С;
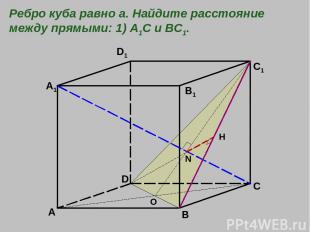
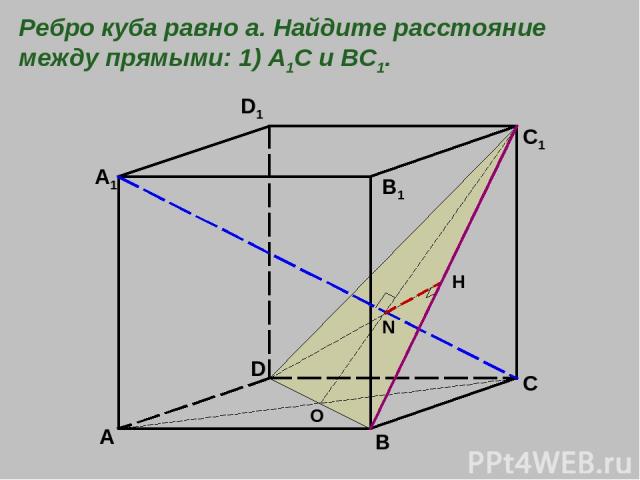
A B C D A1 B1 C1 D1 O N H Ребро куба равно а. Найдите расстояние между прямыми: 1) А1С и ВС1.
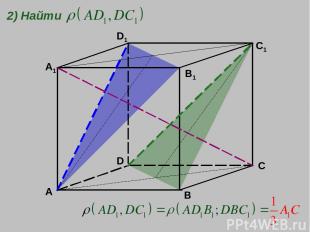
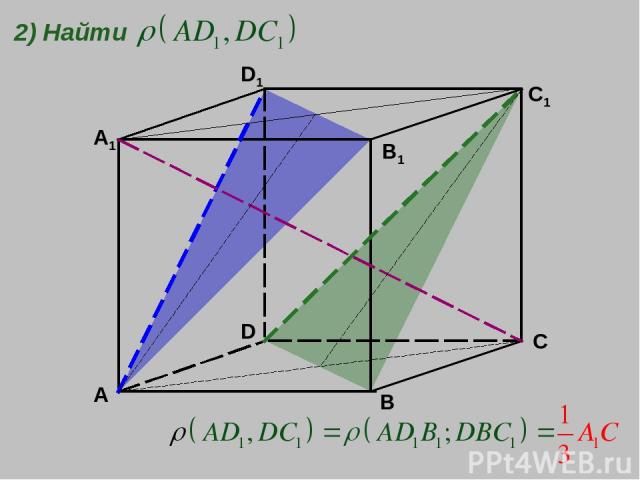
A B C D A1 D1 B1 C1 2) Найти
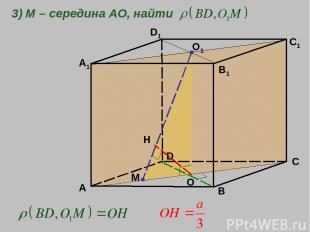
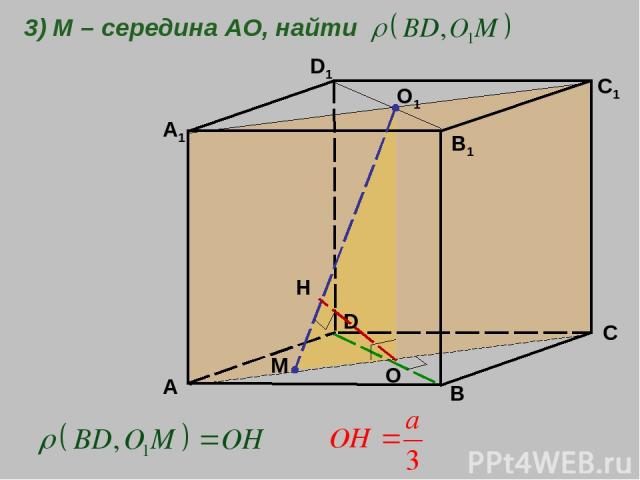
A B C D A1 D1 B1 C1 3) M – середина АО, найти О1 О М Н
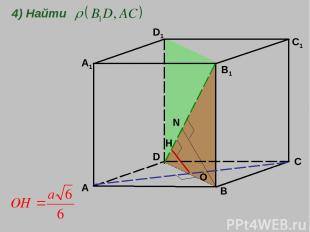
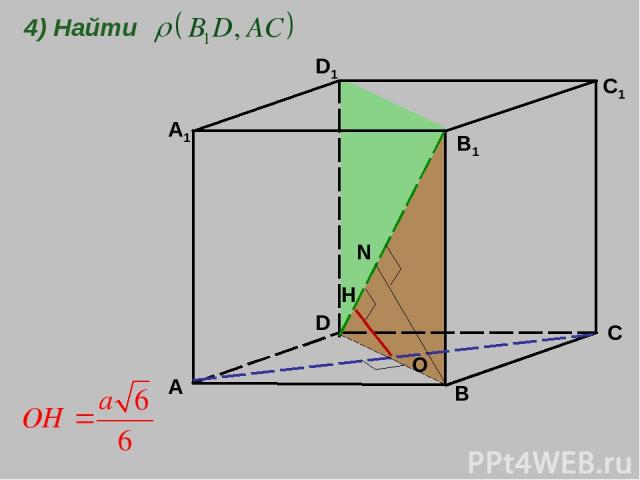
A B C D A1 D1 B1 C1 О Н N 4) Найти
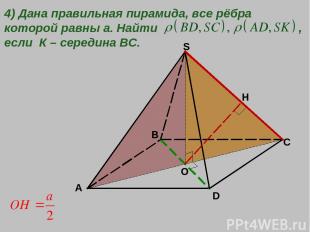
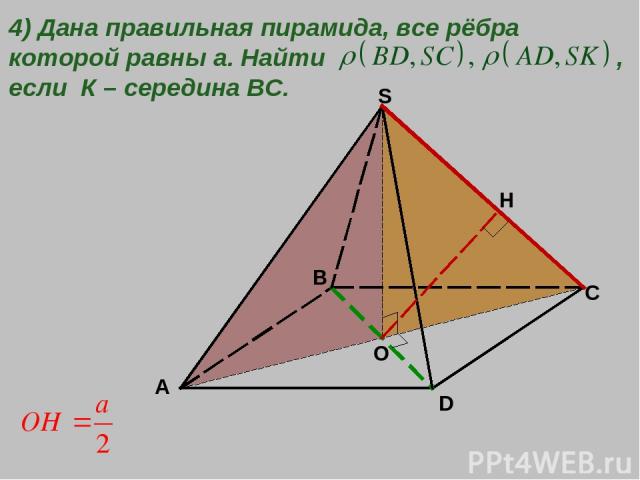
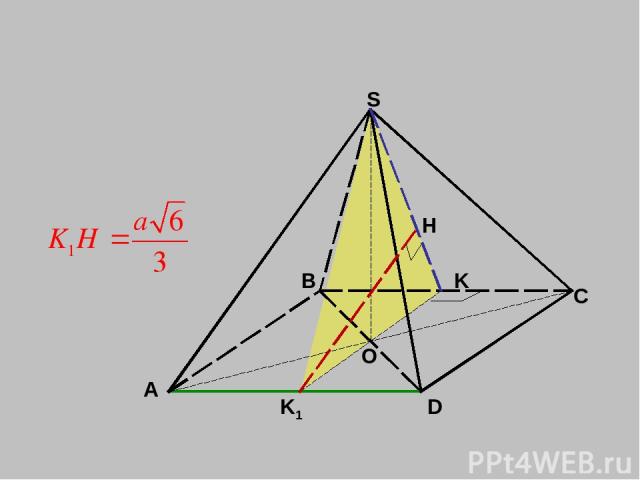
A B C D S O 4) Дана правильная пирамида, все рёбра которой равны а. Найти , если К – середина ВС. H
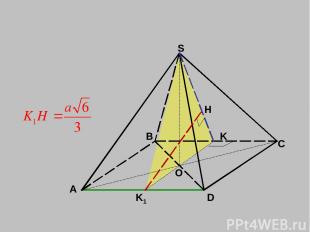
A B C D S O K K1 H
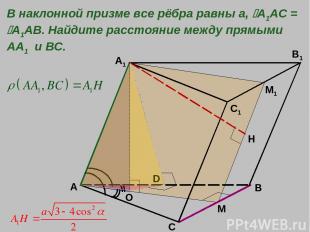
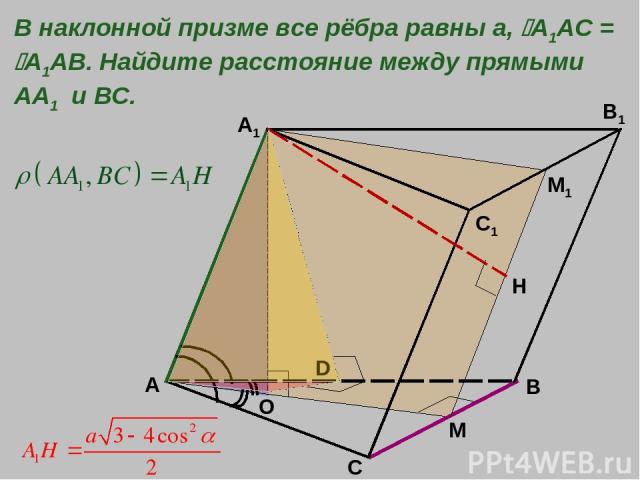
A B C A1 C1 B1 M O В наклонной призме все рёбра равны а, A1AC = A1AB. Найдите расстояние между прямыми АА1 и ВС. М1 Н D