Презентация на тему: Дополнительные построения в трапеции при решении задач
Дополнительные построения в трапеции МБОУ «Средняя общеобразовательная школа № 77» Г. Новокузнецк Кемеровская область Учитель математики Федорова Татьяна Андреевна С А В D K H
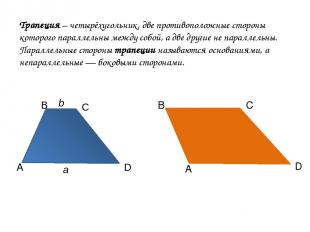
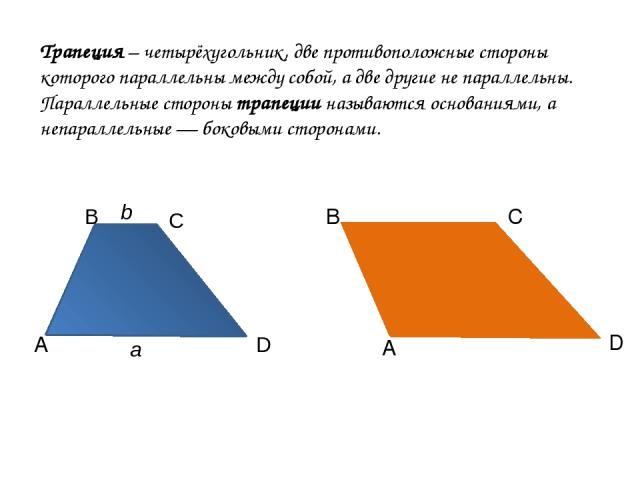
Трапеция – четырёхугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а непараллельные — боковыми сторонами. А А В С D B C D b a
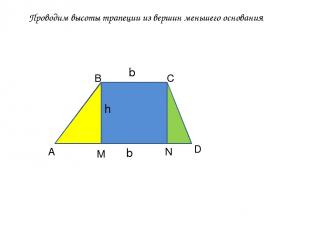
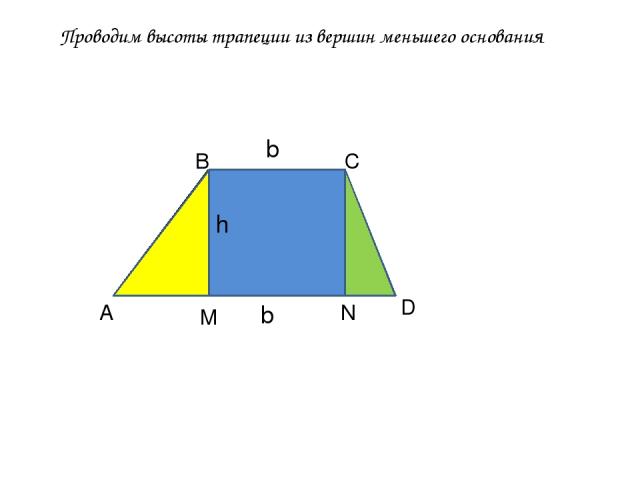
Проводим высоты трапеции из вершин меньшего основания А В С D M N h b b
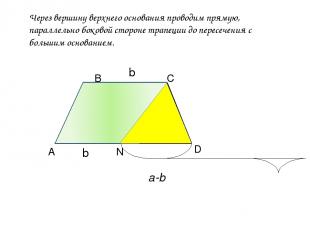
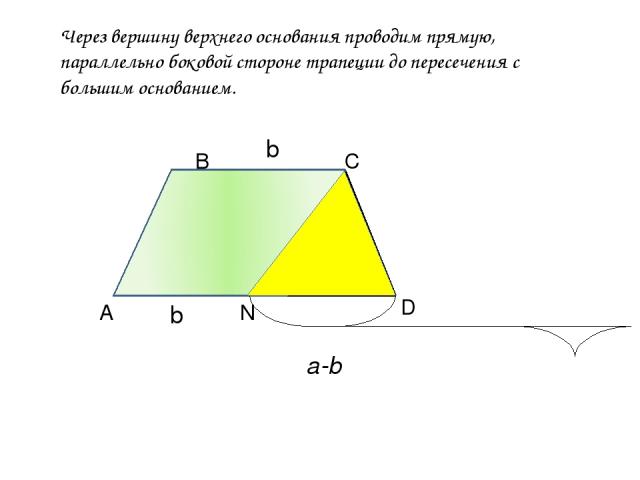
Через вершину верхнего основания проводим прямую, параллельно боковой стороне трапеции до пересечения с большим основанием. А В С D N b b a-b
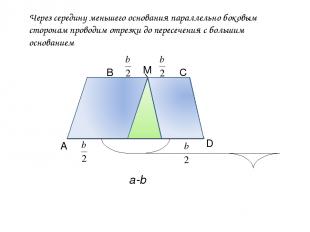
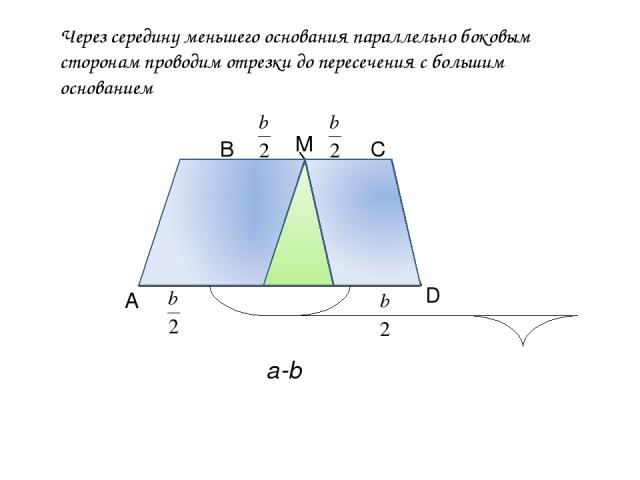
А В С D М Через середину меньшего основания параллельно боковым сторонам проводим отрезки до пересечения с большим основанием a-b
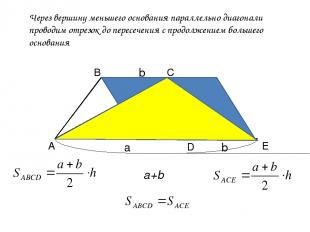
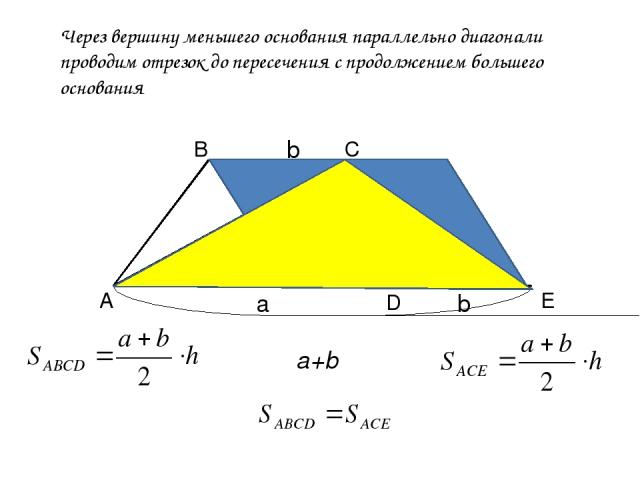
А В С Через вершину меньшего основания параллельно диагонали проводим отрезок до пересечения с продолжением большего основания Е D a b h b a+b
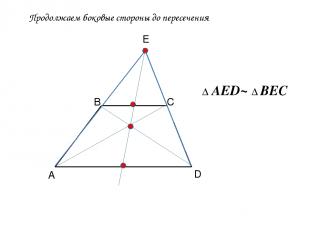
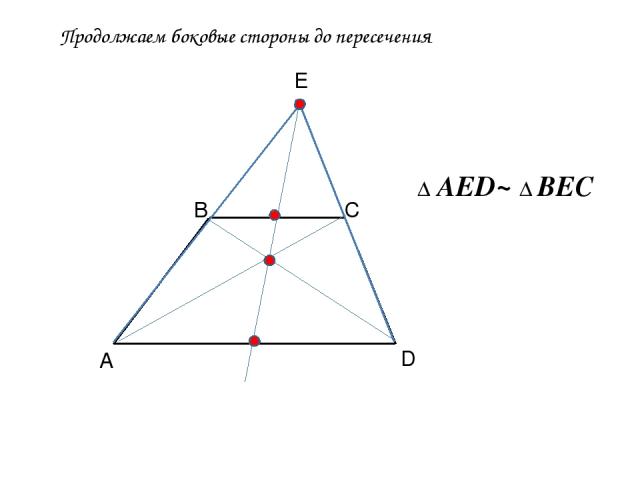
Продолжаем боковые стороны до пересечения А В С D Е Δ AED~ Δ BEC
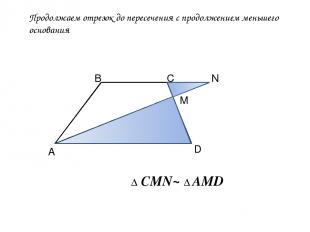
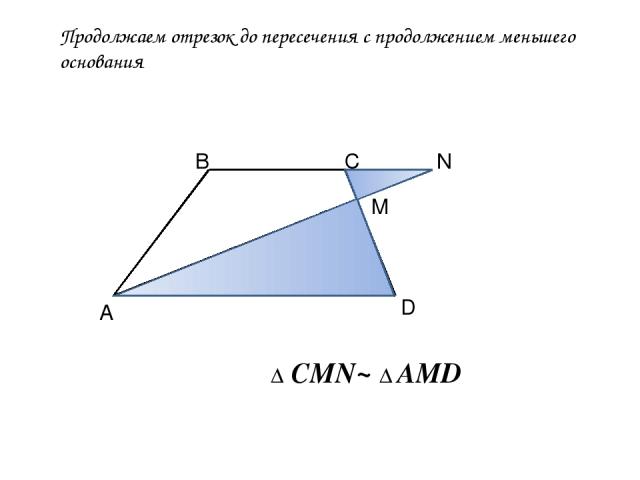
Продолжаем отрезок до пересечения с продолжением меньшего основания А В С D M N Δ CMN~ Δ AMD
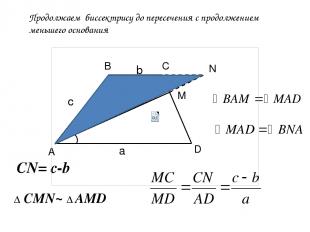
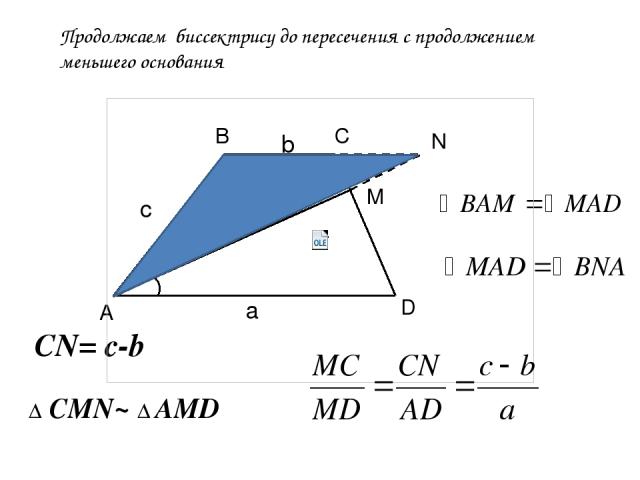
Продолжаем биссектрису до пересечения с продолжением меньшего основания А В С D M N Δ CMN~ Δ AMD a c CN= c-b b

Тренировочные задачи

Задача 1 Найдите площадь трапеции параллельные стороны которой равны 16 и 44, а непараллельные – 17 и 25 A В С D 17 25 16 44 17 K H
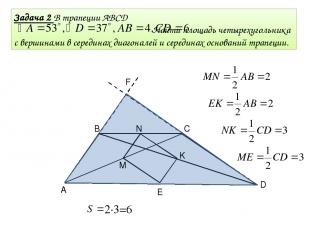
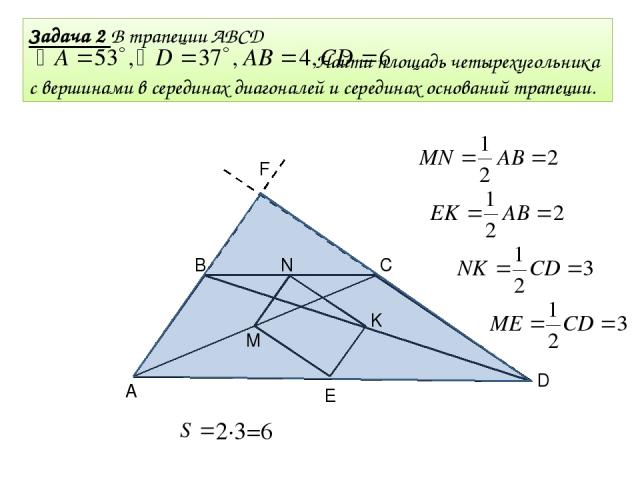
Задача 2 В трапеции ABCD Найти площадь четырехугольника с вершинами в серединах диагоналей и серединах оснований трапеции. В С D F М N K E A 2∙3=6
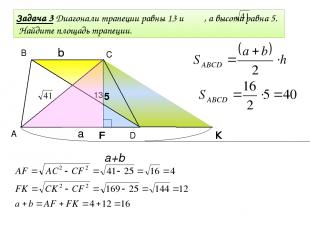
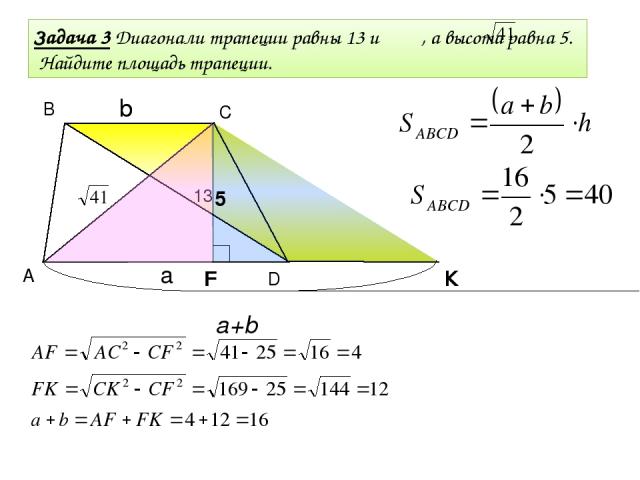
В С К A D Задача 3 Диагонали трапеции равны 13 и , а высота равна 5. Найдите площадь трапеции. 13 5 a+b a b b
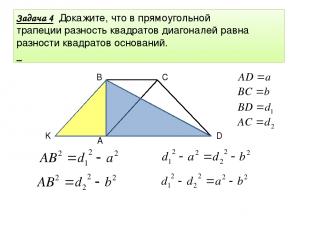
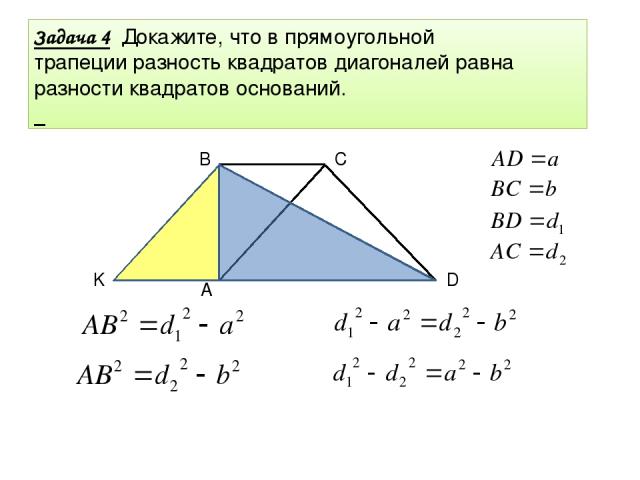
Задача 4 Задача 4 Докажите, что в прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований. D C B A K

Задачи ЕГЭ
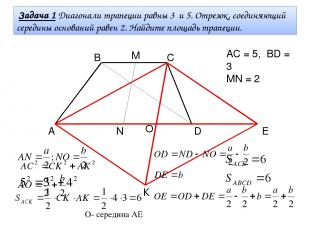
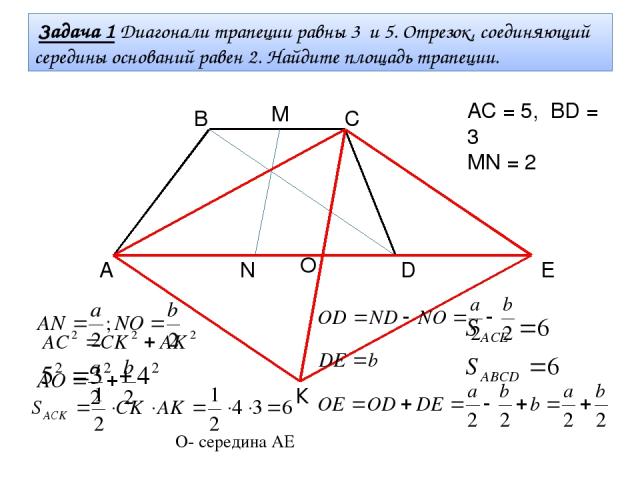
А В С D М N Задача 1 Диагонали трапеции равны 3 и 5. Отрезок, соединяющий середины оснований равен 2. Найдите площадь трапеции. Е АС = 5, ВD = 3 МN = 2 О К O- середина АЕ