Презентация на тему: Площадь криволинейной трапеции

Площадь криволинейной трапеции

Определение производной: Найти производную функции по определению:

Вставьте вместо * Определение первообразной:

Будут ли первообразными следующие функции для функции

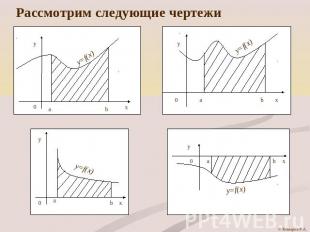
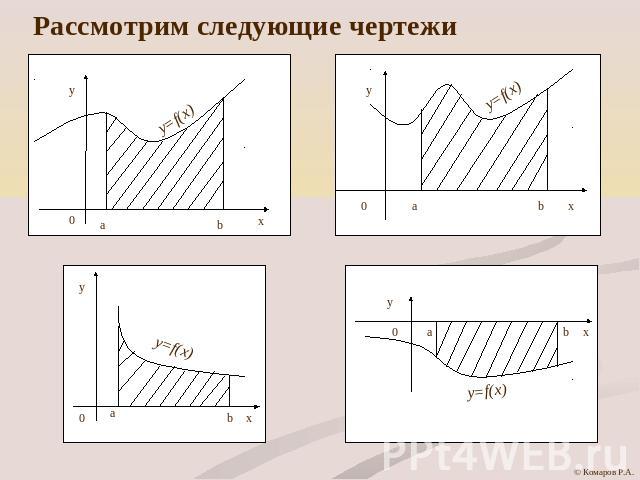
Рассмотрим следующие чертежи

Определение: фигура, ограниченная графиком непрерывной и не меняющей своего знака на отрезке [a; b] функции, прямыми x=a, x=b и отрезком [a; b] называется криволинейной трапецией.

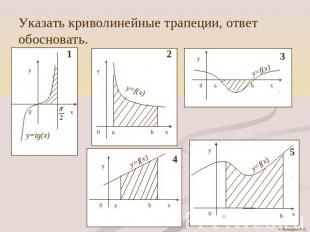
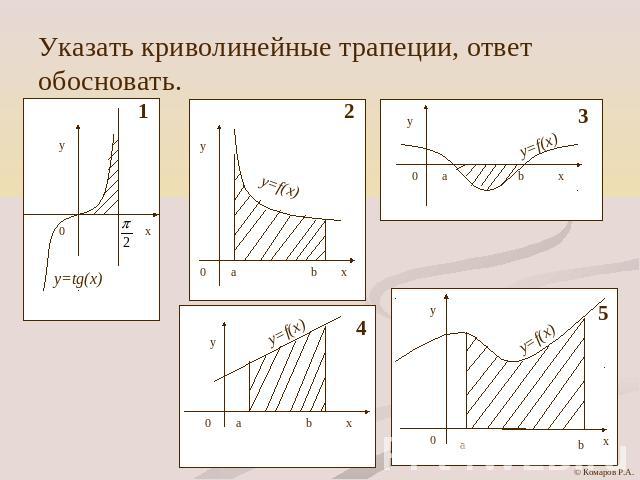
Указать криволинейные трапеции, ответ обосновать.

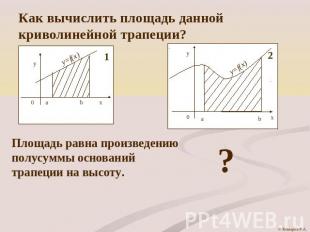
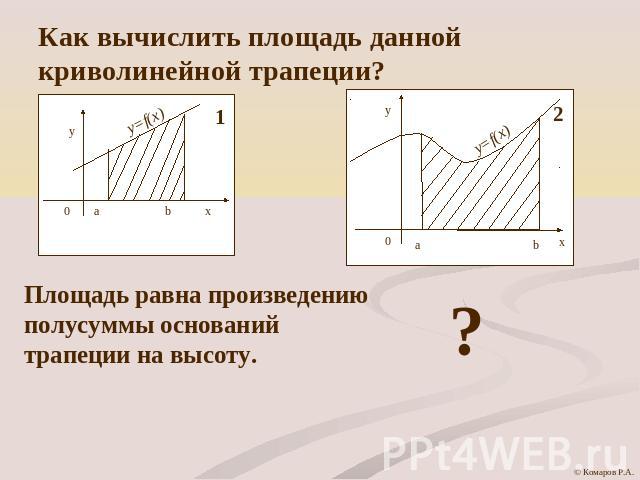
Как вычислить площадь данной криволинейной трапеции? Площадь равна произведениюполусуммы основанийтрапеции на высоту.

Площадь криволинейной трапеции

Вычислите площадь криволинейной трапеции 2-мя способами 1) Используя формулу площадитрапеции из геометрии, получим:2) Найдите F(x) и вычислите S по формуле S=F(b)-F(a)

Теорема:Если f – непрерывная и неотрицательная на отрезке [a; b] функция, а F – ее первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a; b], т.е. S=F(b)-F(a). Дано: f – функция непрерывная, неотрицательная на отрезке [a; b]криволинейная трапеция Док-ть: S=F(b)-F(a)

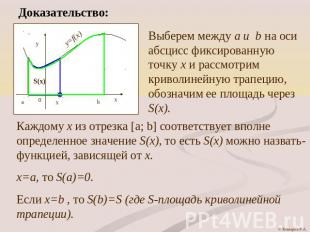
Доказательство: Выберем между a и b на оси абсцисс фиксированную точку х и рассмотрим криволинейную трапецию, обозначим ее площадь через S(x).Каждому х из отрезка [a; b] соответствует вполне определенное значение S(x), то есть S(x) можно назвать- функцией, зависящей от х. х=а, то S(a)=0.Если х=b , то S(b)=S (где S-площадь криволинейной трапеции).

– это площадь криволинейной трапеции, опирающейся на отрезок[x; x+∆x] (площадь фигуры заштрихованной на рисунке)

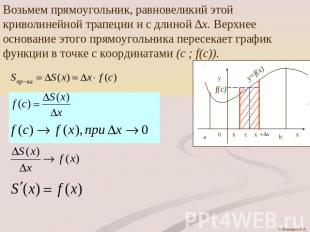
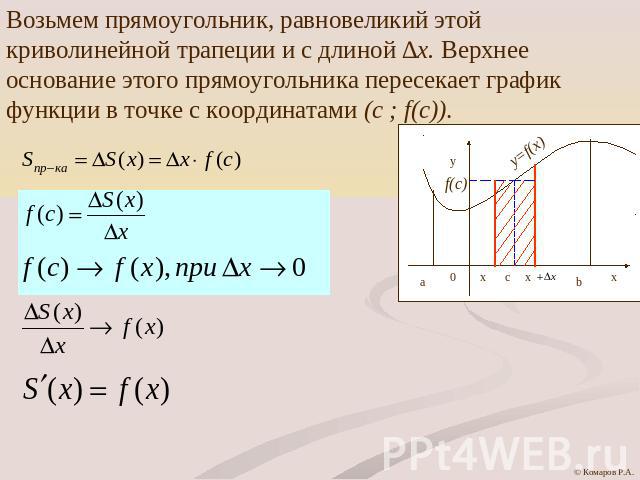
Возьмем прямоугольник, равновеликий этой криволинейной трапеции и с длиной ∆х. Верхнее основание этого прямоугольника пересекает график функции в точке с координатами (с ; f(c)).

Таким образом, мы доказали теорему и в дальнейшем площадь криволинейной трапециибудем вычислять по формуле

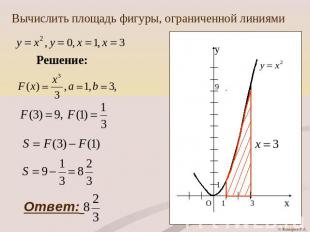
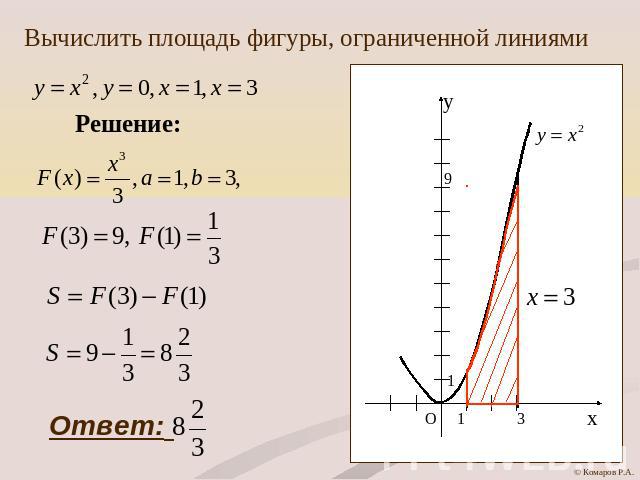
Вычислить площадь фигуры, ограниченной линиями

Алгоритм нахождения площадикриволинейной трапеции:Изобразить чертеж и убедится, является ли данная фигура криволинейной трапециейНайти первообразную F(x)Применить формулу S=F(b)-F(a)