Презентация на тему: Площадь криволинейной трапеции и интеграл

Площадь криволинейной трапеции и интеграл. 900igr.net

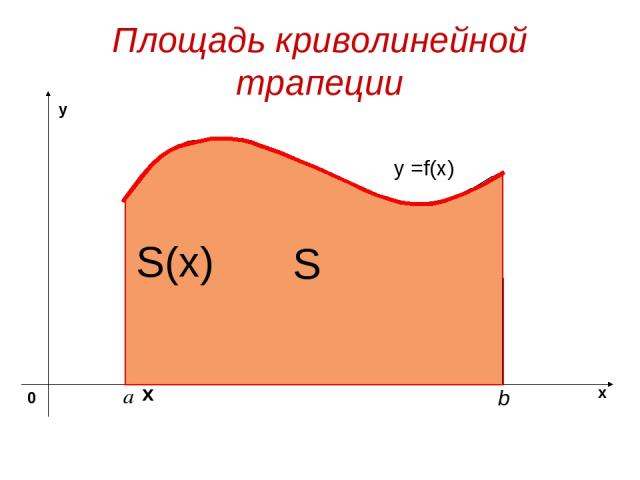
Площадь криволинейной трапеции y =f(x) S х S(x)

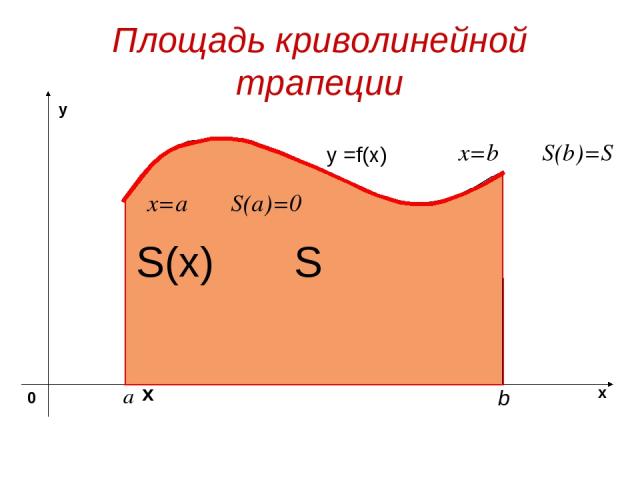
Площадь криволинейной трапеции y =f(x) S х S(x) x=a S(a)=0 x=b S(b)=S

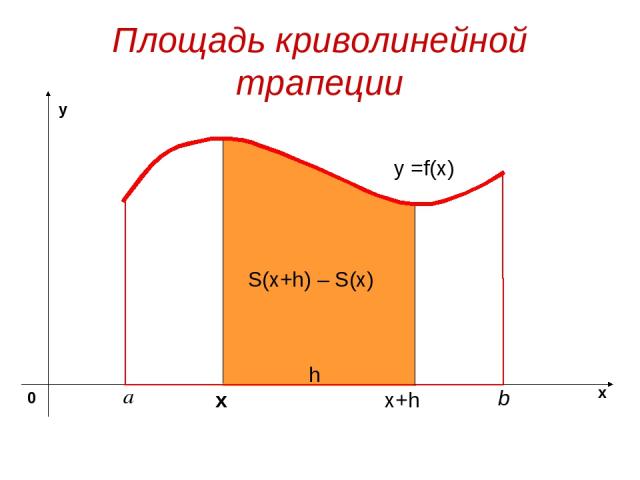
Площадь криволинейной трапеции y =f(x) х S(x+h) – S(x) x+h h

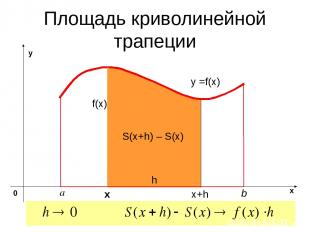
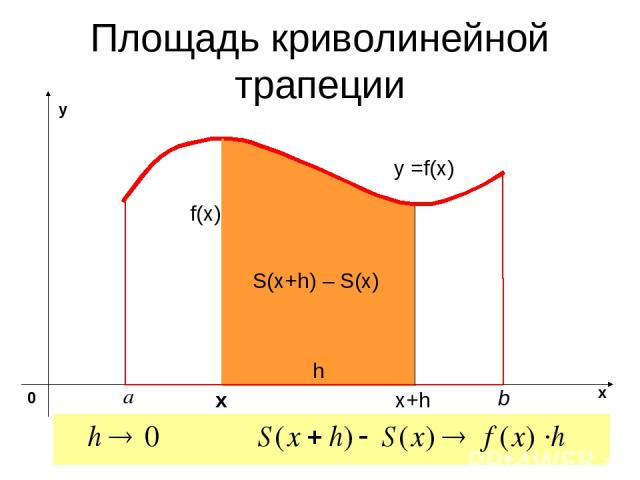
Площадь криволинейной трапеции y =f(x) х S(x+h) – S(x) x+h h f(x)

Площадь криволинейной трапеции

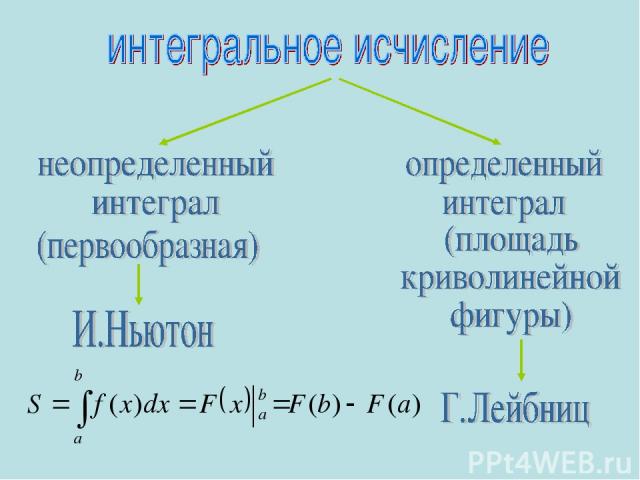
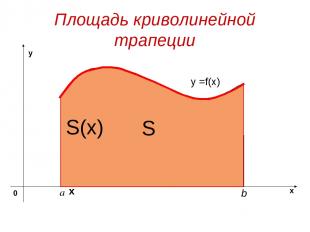
Фигура, ограниченная снизу отрезком [a, b] оси Ох ,сверху графиком непрерывной функции у= f(x), принимающей положительные значения , а с боков отрезками прямых х = а, х =b называется криволинейной трапецией.

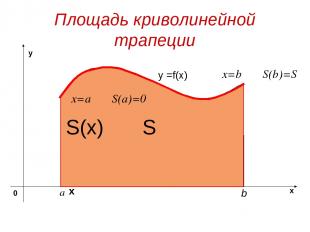
Обозначим S(х) - площадь криволинейной трапеции с основанием [a, х] , х - любая точка отрезка [a, b] При х = а отрезок [a, х] вырождается в точку, поэтому S(а) = 0; при х = b, S(b) = S

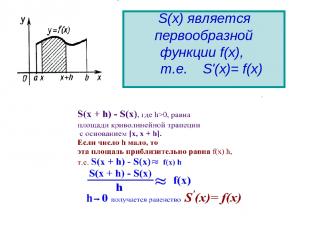
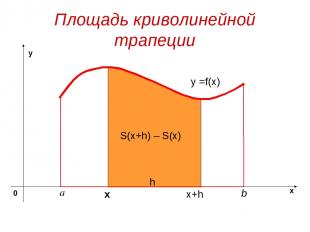
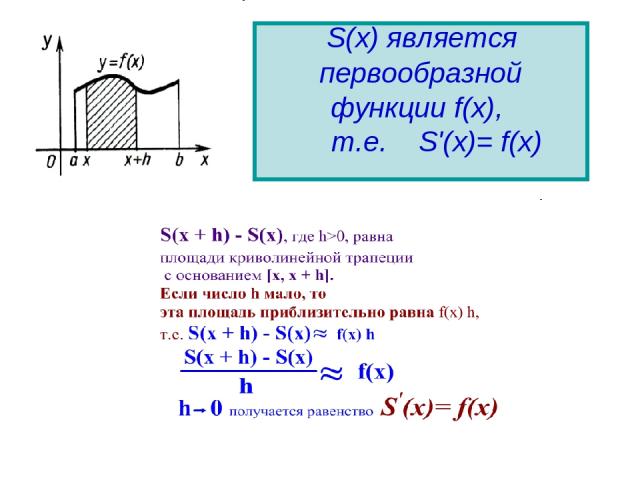
S(х) является первообразной функции f(x), т.е. S'(х)= f(x)

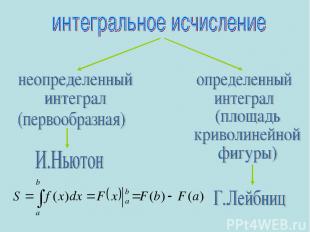
Площадь криволинейной трапеции вычисляется по формуле S = F(b) - F(a) Разность F(b) - F(a) называют интегралом от функции f(x) на отрезке [a, b] и обозначают так :

Любая другая первообразная F(x) отличается от S(x) на постоянную, т.е. F(x) = S(x) + С При х = а получаем F(a) = S(a) + C Так как S(a) = 0 , то С = F(a) и равенство F(x) = S(x) + С можно записать так S(x) = F(x) - F(a), отсюда при х =b получим S(b) = F(b) - F(a)

Немного истории -1675 г, опубликовано в 1686 г ввел Г.Лейбниц - 1675 г, Ж Лагранж 5 век до н.э. др.гр. ученый Демокрит 3-4 век до н.э. Архимед ввел метод исчерпывания

Лейбниц Готфрид Вильгельм (1646-1716) « Общее искусство знаков представляет чудесное пособие, так как оно разгружает воображение… Следует заботиться о том, чтобы обозначения были удобны для открытий. Обозначения коротко выражают и отображают сущность вещей. Тогда поразительным образом сокращается работа мысли.» Лейбниц

Исаак Ньютон (1643-1727)

Немного истории «Интеграл» придумал Я.Бернулли (1690) «восстанавливать» от латинского integro «целый» от латинского integer

Площадь фигуры Объем тела вращения Работа электрического заряда Работа переменной силы Центр масс

В классе: № 999(1,3) № 1000(1,2)

Дома: П 56 № 999(2,4) № 1000(3)