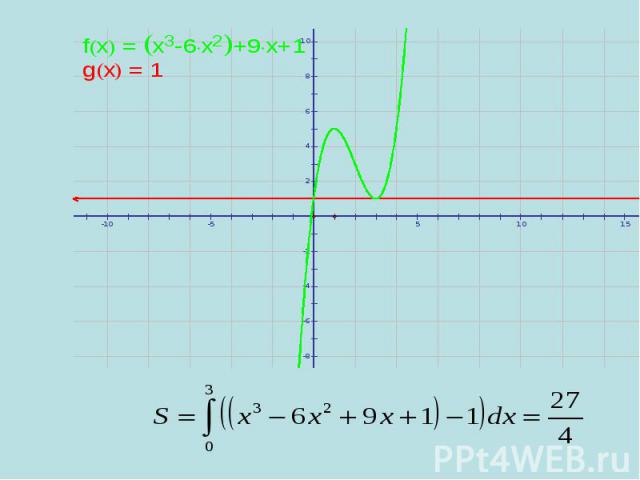
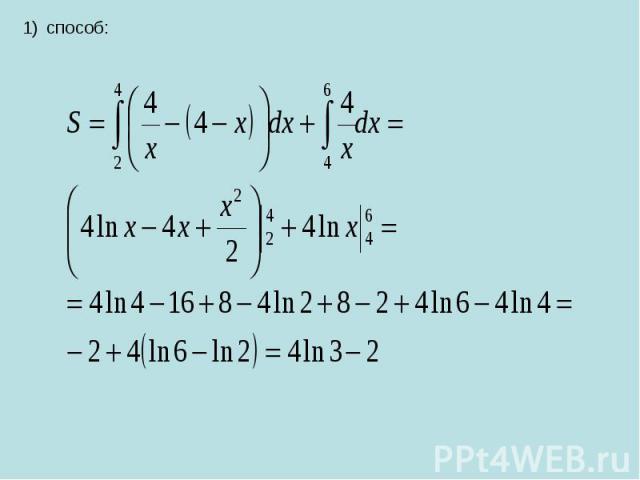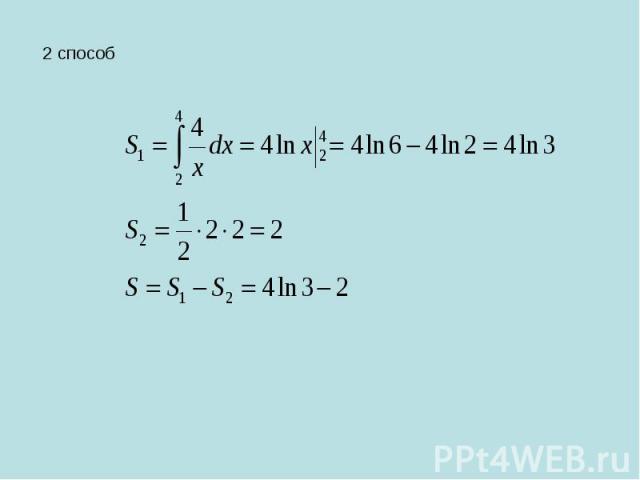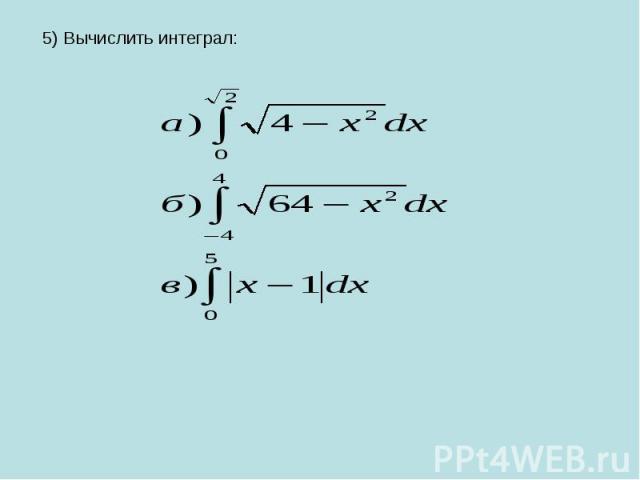Презентация на тему: Площадь криволинейной трапеции

площадь криволинейной трапеции

Площадь криволинейной трапеции
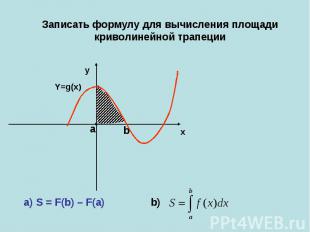
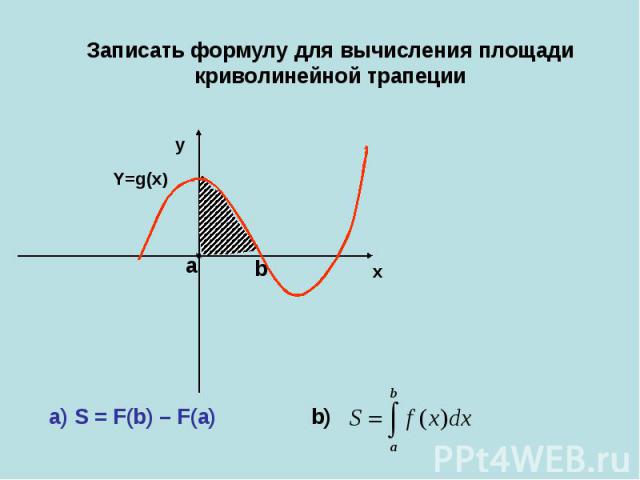
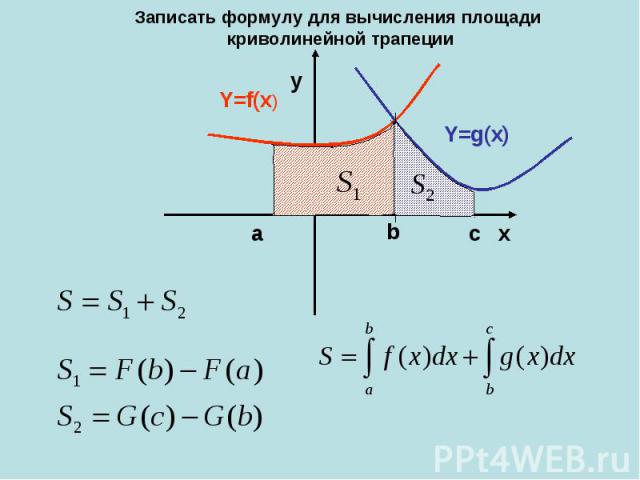
Записать формулу для вычисления площади криволинейной трапеции
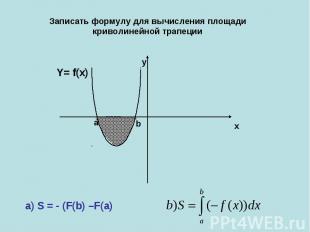
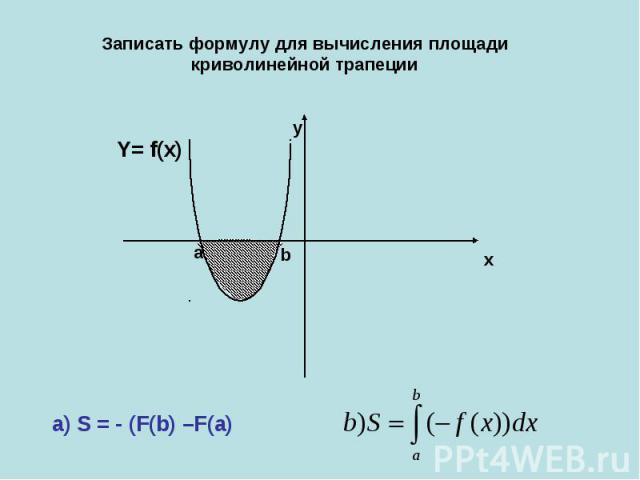
Записать формулу для вычисления площади криволинейной трапеции
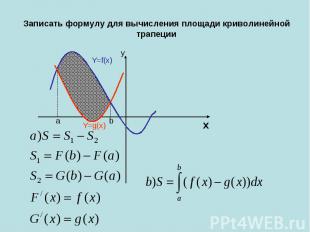
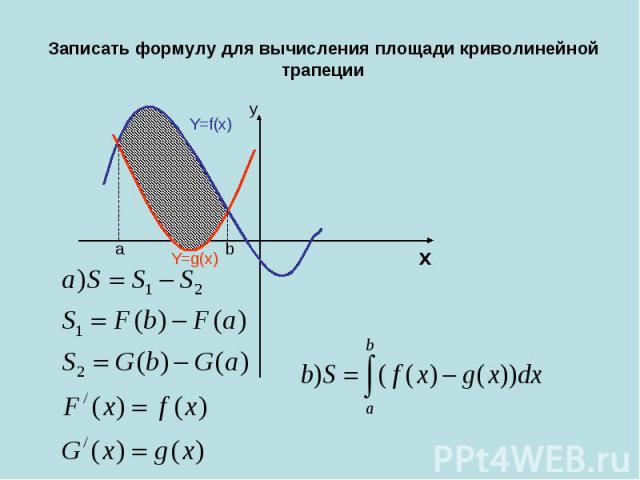
Записать формулу для вычисления площади криволинейной трапеции
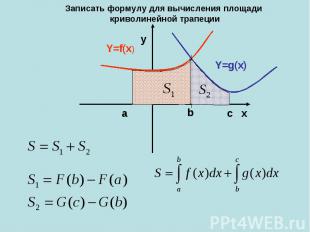
Записать формулу для вычисления площади криволинейной трапеции
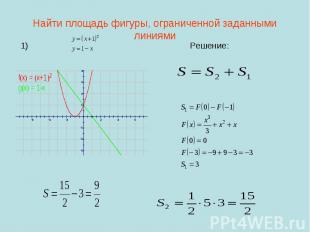
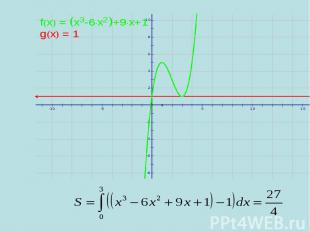
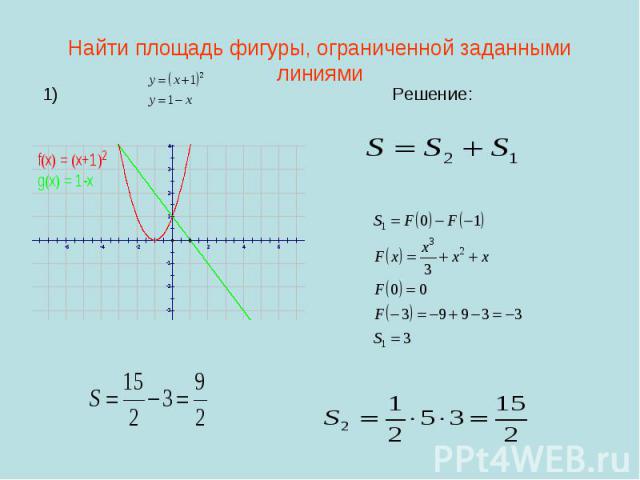
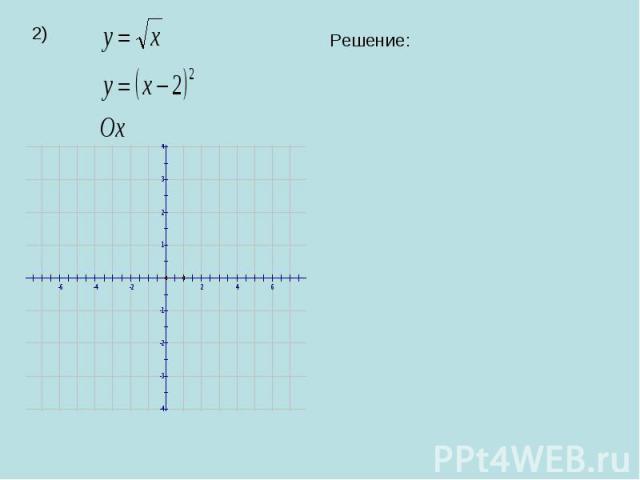
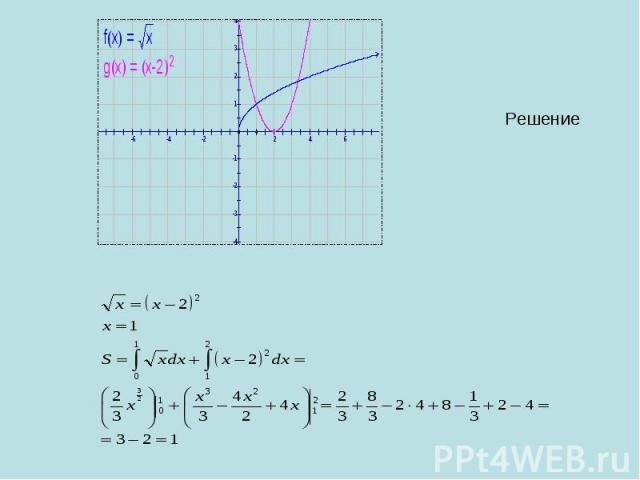
Найти площадь фигуры, ограниченной заданными линиями
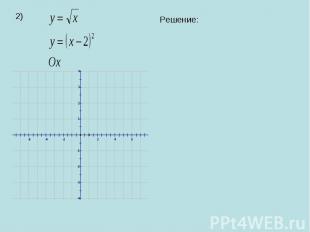
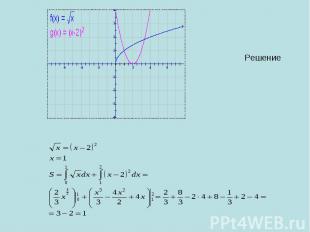
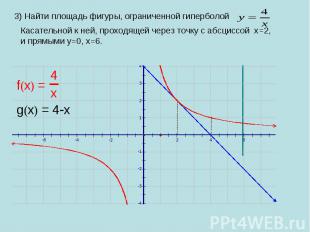
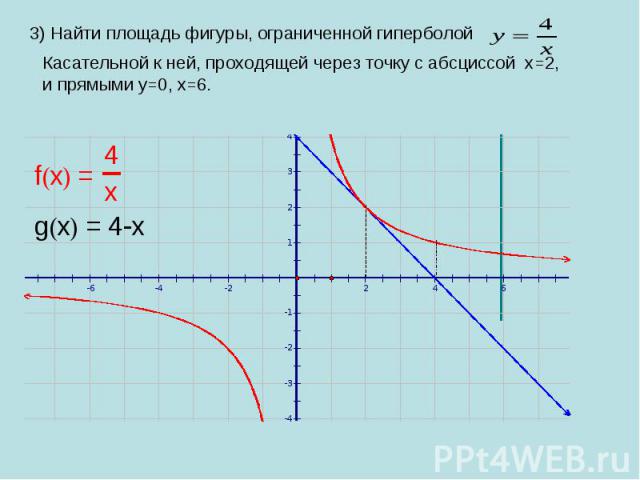
3) Найти площадь фигуры, ограниченной гиперболой Касательной к ней, проходящей через точку с абсциссой х=2, и прямыми у=0, х=6.
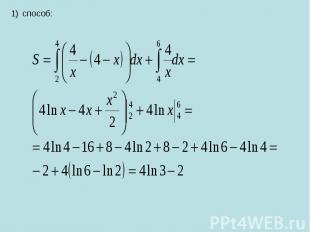
способ:
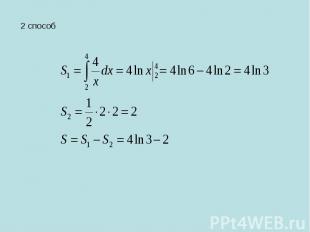
2 способ
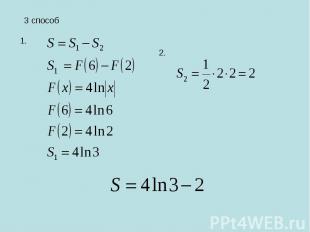
3 способ
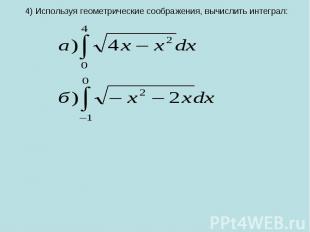
4) Используя геометрические соображения, вычислить интеграл:

Решение. а) Имеем: Это уравнение окружности радиуса r=2 с центром в точке (2;0).Значит, заданным интегралом выражается площадь половины круга.
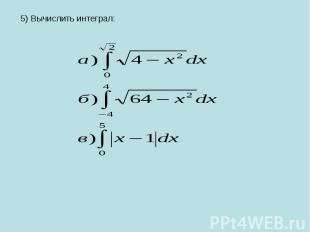
5) Вычислить интеграл:

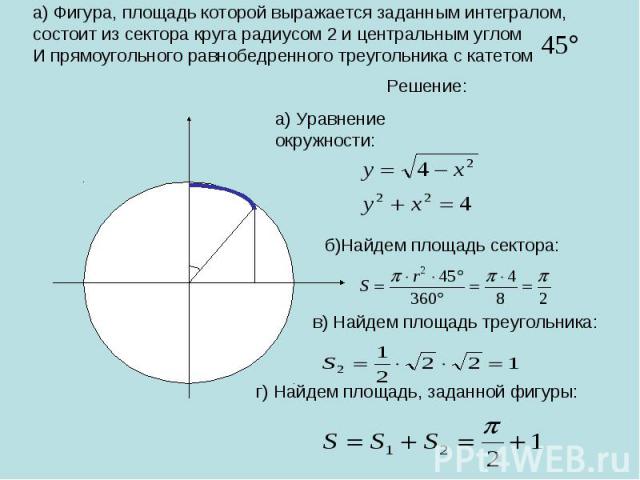
а) Фигура, площадь которой выражается заданным интегралом, состоит из сектора круга радиусом 2 и центральным углом И прямоугольного равнобедренного треугольника с катетом
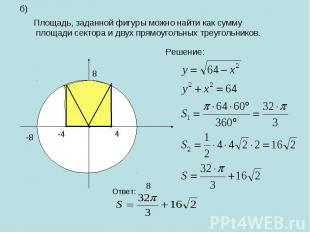
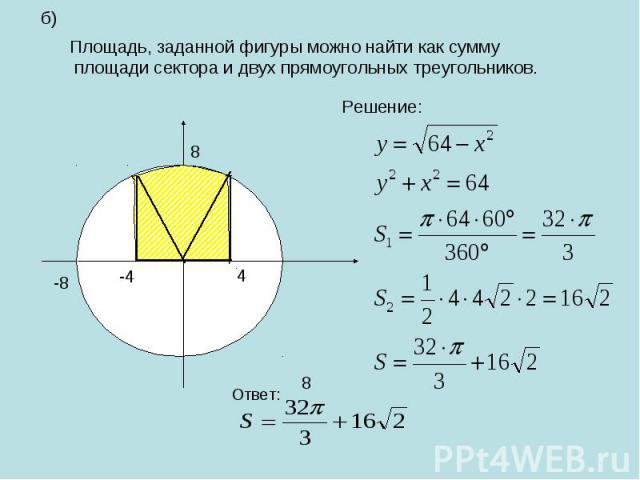
Площадь, заданной фигуры можно найти как сумму площади сектора и двух прямоугольных треугольников.
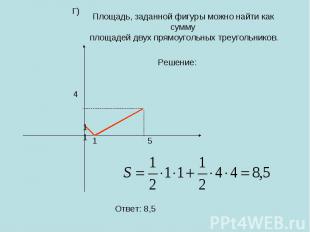
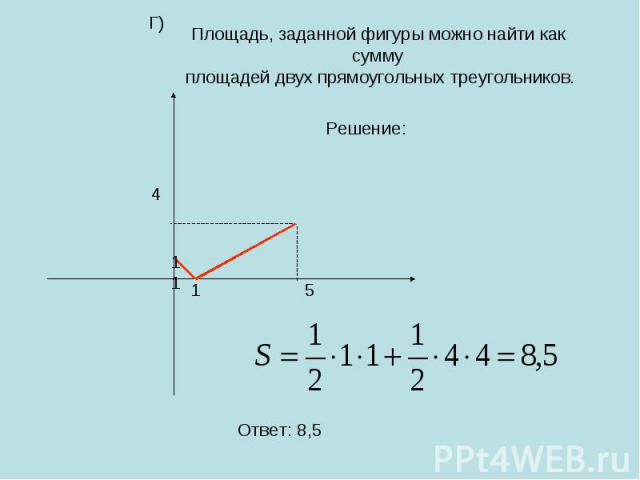
Площадь, заданной фигуры можно найти как сумму площадей двух прямоугольных треугольников.
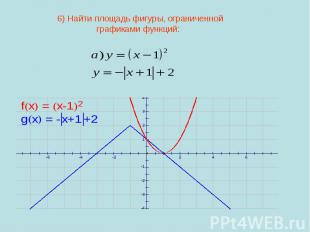
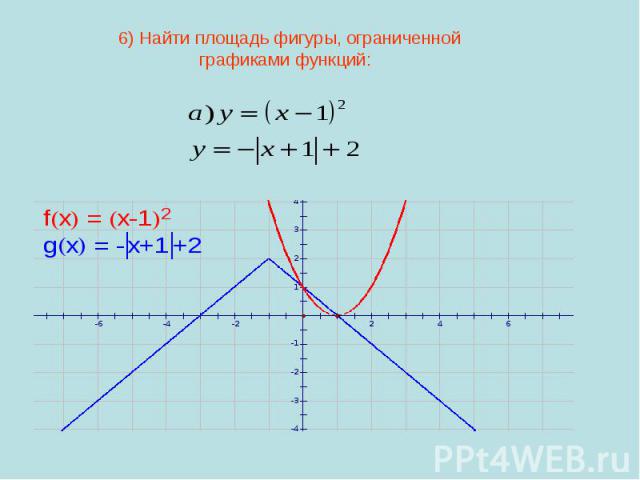
6) Найти площадь фигуры, ограниченнойграфиками функций:

Решение:Найти площадь фигуры,ограниченной графикомфункции и касательной к нему в точке х=3Заданная функция имеет точку максимума (1;5) и точку минимума(3;1).Построим график этой функции. Касательная к нему в точке х=3 параллельна оси абсцисс и имеет с графиком еще одну общую точку (0;1).