Презентация на тему: Теорема о трех перпендикулярах (10 класс)

Теорема о трех перпендикулярах Геометрия 10 Методическая разработка Савченко Е.М.МОУ гимназия №1, г. Полярные Зори, Мурманской обл.

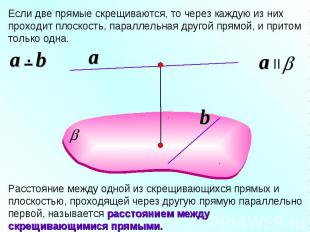
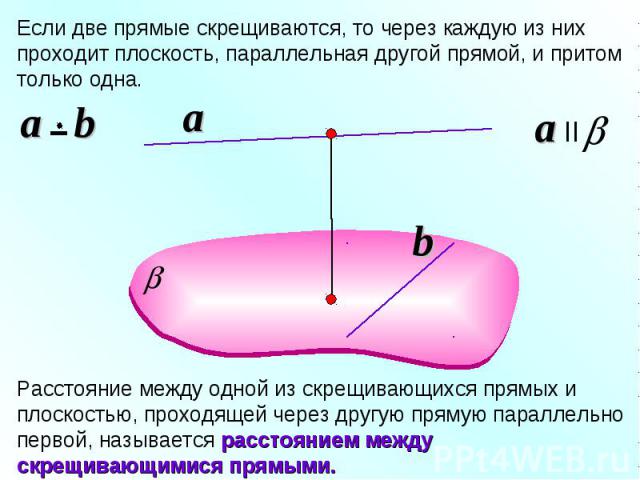
Если две прямые скрещиваются, то через каждую из них проходит плоскость, параллельная другой прямой, и притом только одна. Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

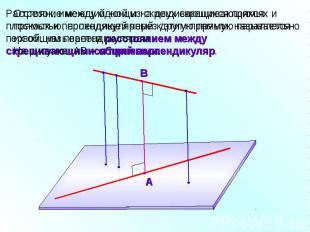
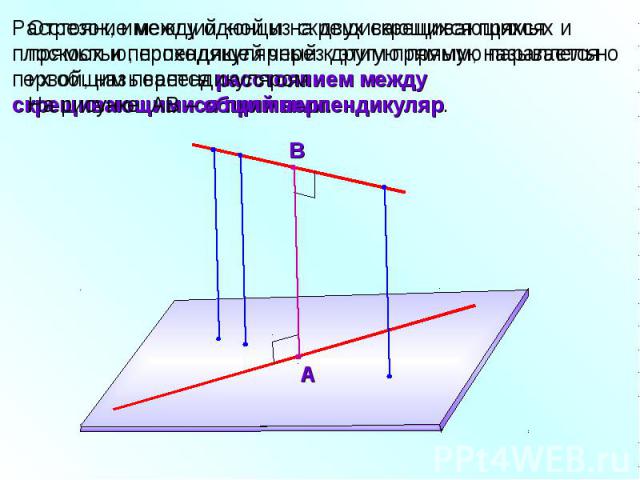
Отрезок, имеющий концы на двух скрещивающихся прямых и перпендикулярный к этим прямым, называется их общим перпендикуляром. На рисунке АВ – общий перпендикуляр.Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.

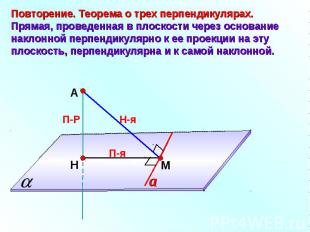
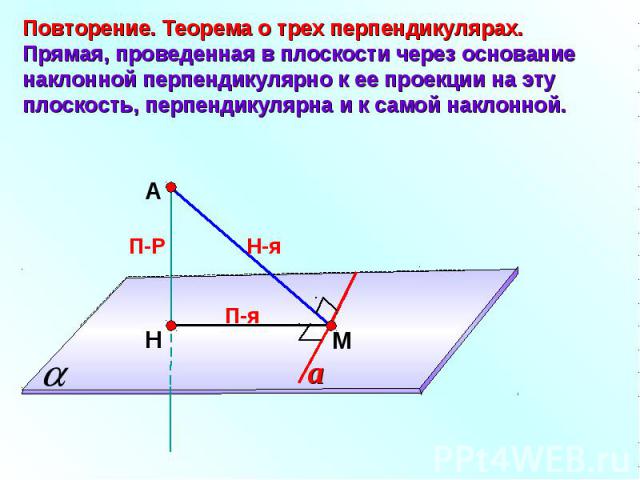
Повторение. Теорема о трех перпендикулярах.Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

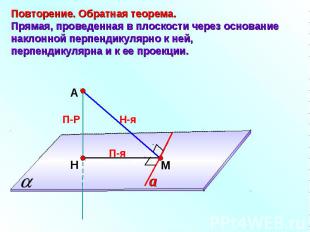
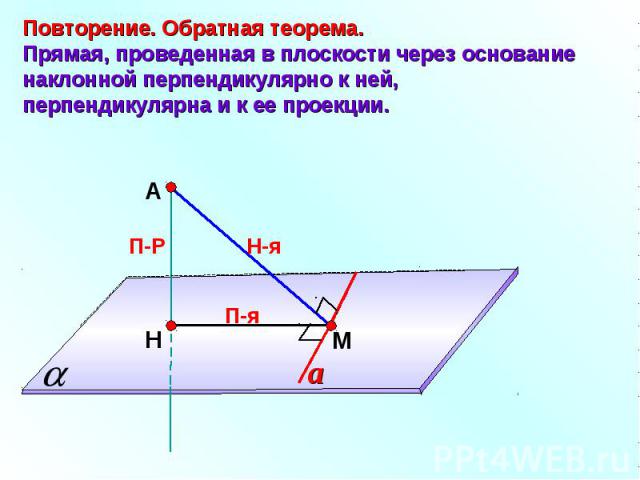
Повторение. Обратная теорема.Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.

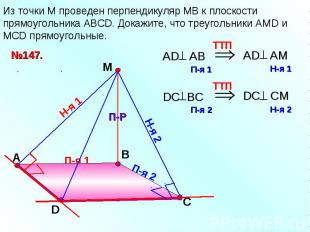
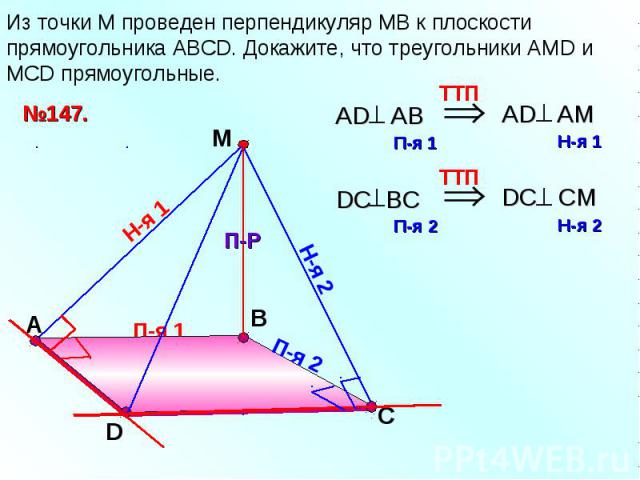
Из точки М проведен перпендикуляр МВ к плоскости прямоугольника АВСD. Докажите, что треугольники АМD и МСD прямоугольные.

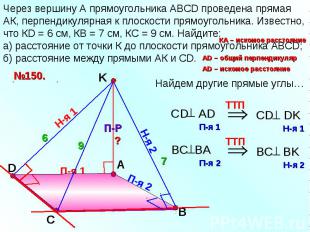
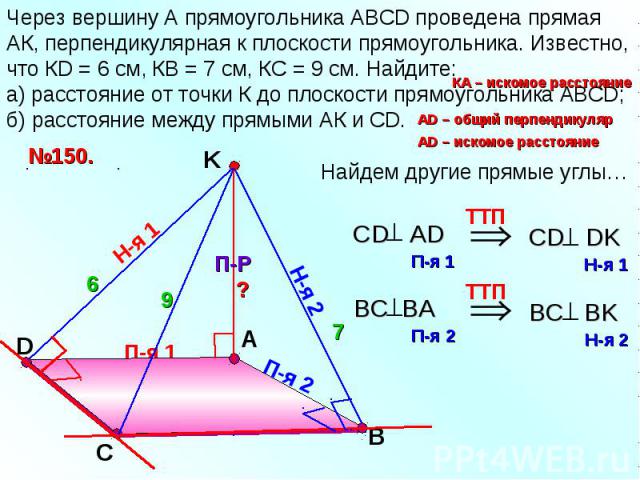
Через вершину А прямоугольника АВСD проведена прямая АК, перпендикулярная к плоскости прямоугольника. Известно, что КD = 6 см, КВ = 7 см, КС = 9 см. Найдите: а) расстояние от точки К до плоскости прямоугольника АВСD; б) расстояние между прямыми АК и СD.

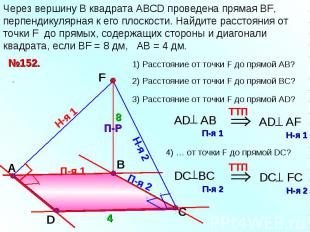
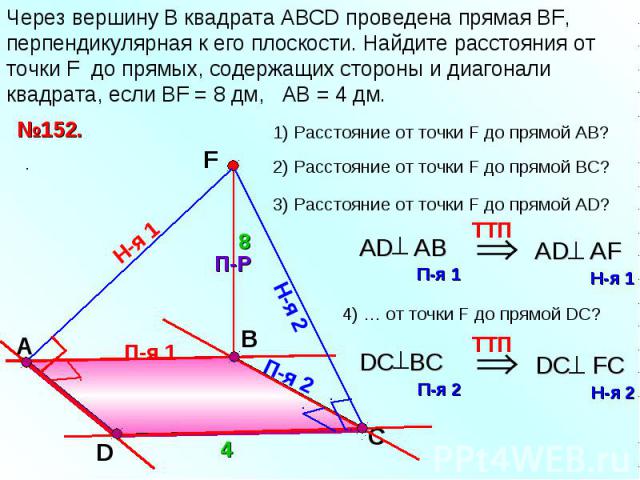
Через вершину B квадрата АВСD проведена прямая ВF, перпендикулярная к его плоскости. Найдите расстояния от точки F до прямых, содержащих стороны и диагонали квадрата, если ВF = 8 дм, АВ = 4 дм.

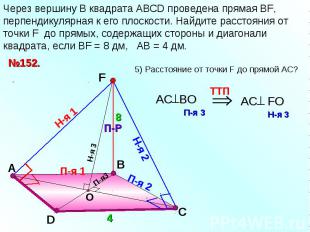
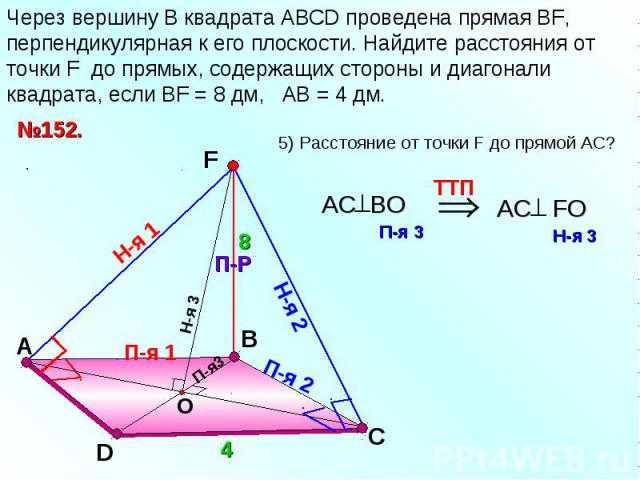
Через вершину B квадрата АВСD проведена прямая ВF, перпендикулярная к его плоскости. Найдите расстояния от точки F до прямых, содержащих стороны и диагонали квадрата, если ВF = 8 дм, АВ = 4 дм.

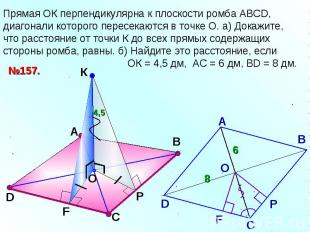
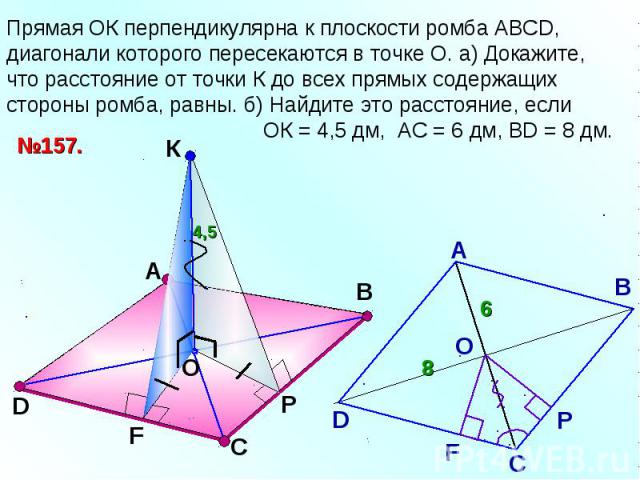
Прямая ОК перпендикулярна к плоскости ромба АВСD, диагонали которого пересекаются в точке О. а) Докажите, что расстояние от точки К до всех прямых содержащих стороны ромба, равны. б) Найдите это расстояние, если ОК = 4,5 дм, АС = 6 дм, ВD = 8 дм.

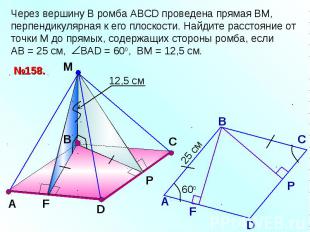
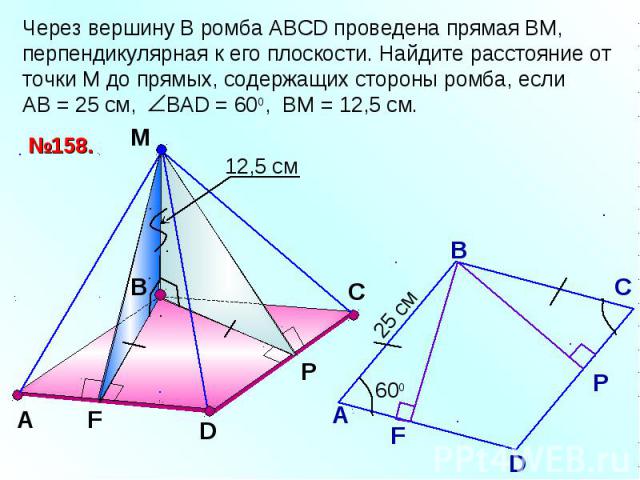
Через вершину В ромба АВСD проведена прямая ВМ, перпендикулярная к его плоскости. Найдите расстояние от точки М до прямых, содержащих стороны ромба, если АВ = 25 см, ВАD = 600, ВМ = 12,5 см.

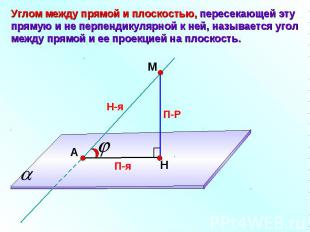
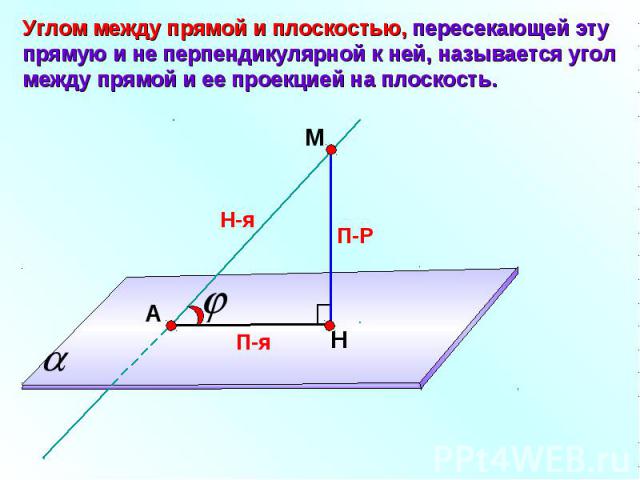
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.

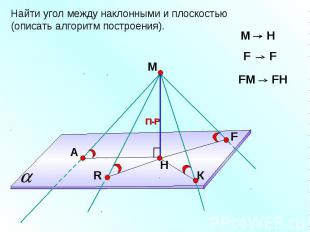
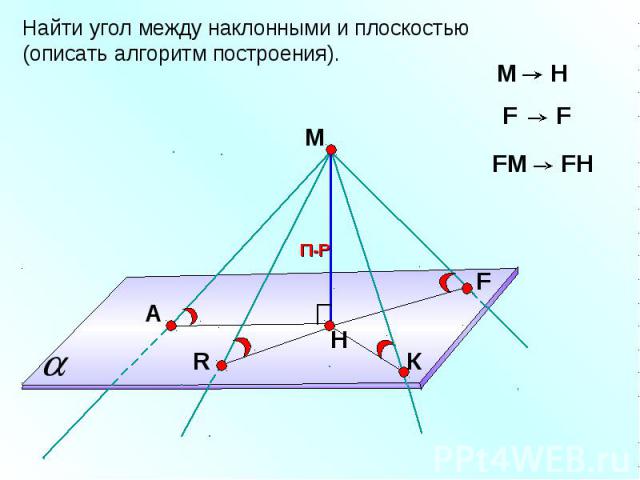
Найти угол между наклонными и плоскостью (описать алгоритм построения).

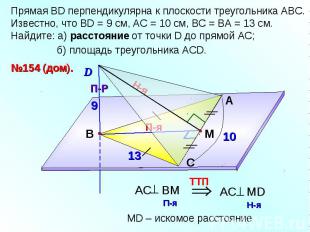
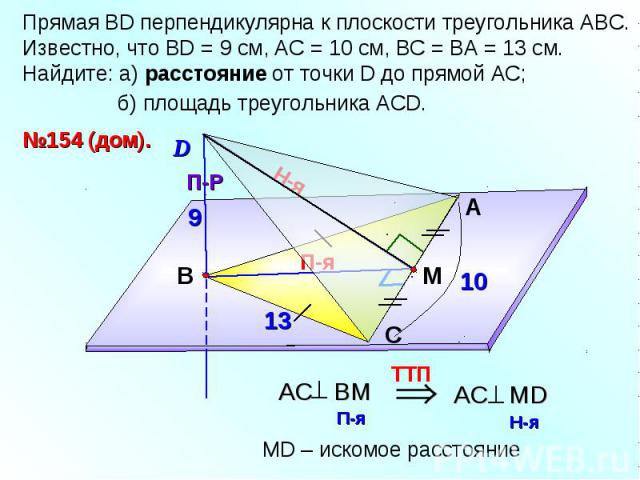
Прямая ВD перпендикулярна к плоскости треугольника АВС. Известно, что ВD = 9 см, АС = 10 см, ВС = ВА = 13 см. Найдите: а) расстояние от точки D до прямой АС; б) площадь треугольника АСD.

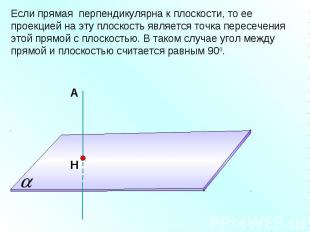
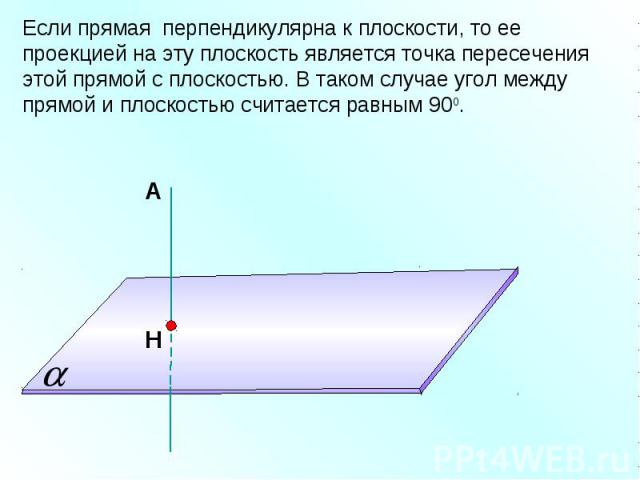
Если прямая перпендикулярна к плоскости, то ее проекцией на эту плоскость является точка пересечения этой прямой с плоскостью. В таком случае угол между прямой и плоскостью считается равным 900.

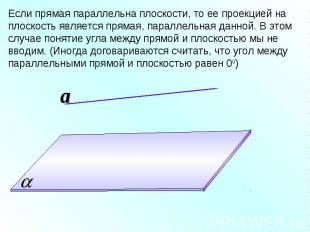
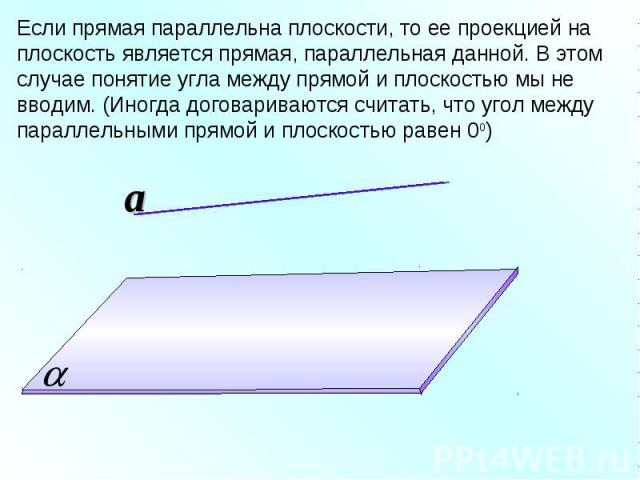
Если прямая параллельна плоскости, то ее проекцией на плоскость является прямая, параллельная данной. В этом случае понятие угла между прямой и плоскостью мы не вводим. (Иногда договариваются считать, что угол между параллельными прямой и плоскостью равен 00)

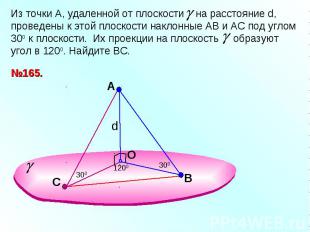
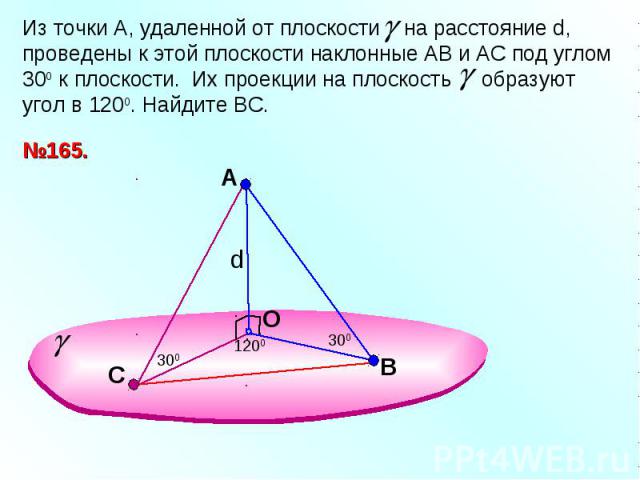
Из точки А, удаленной от плоскости на расстояние d, проведены к этой плоскости наклонные АВ и АС под углом 300 к плоскости. Их проекции на плоскость образуют угол в 1200. Найдите ВС.