Презентация на тему: Теорема о трёх перпендикулярах. Чертежи к решению некоторых задач

Теорема о трёх перпендикулярахЧертежи к решению некоторых задач Подготовил учащийся группы a 2-11 курс II«Колледж сервиса и туризма»Бессонов Олег
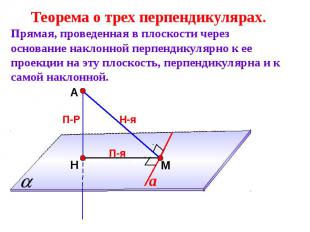
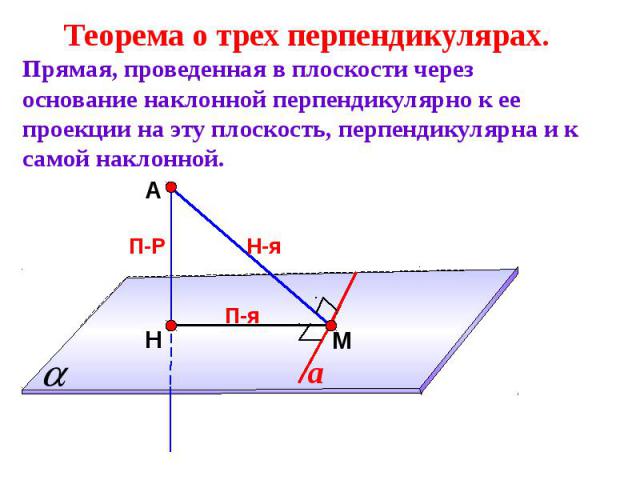
Теорема о трех перпендикулярах.Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
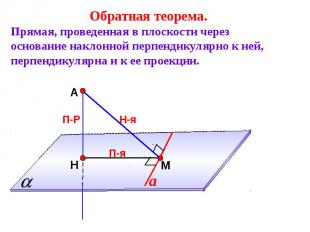
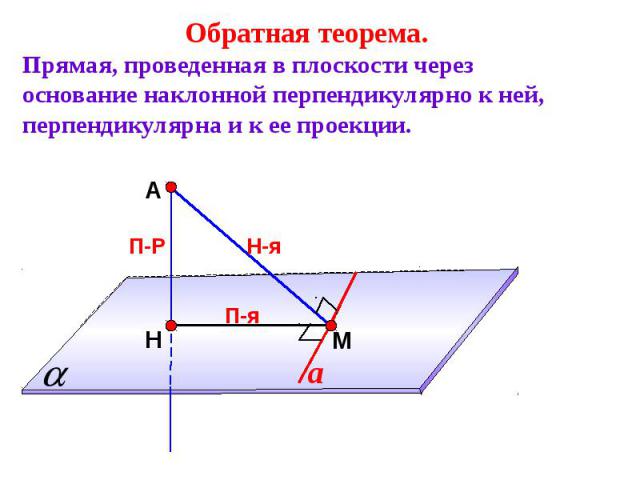
Обратная теорема.Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
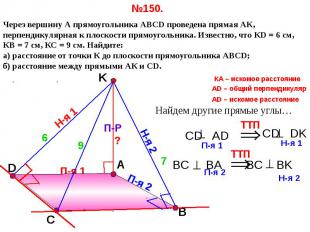
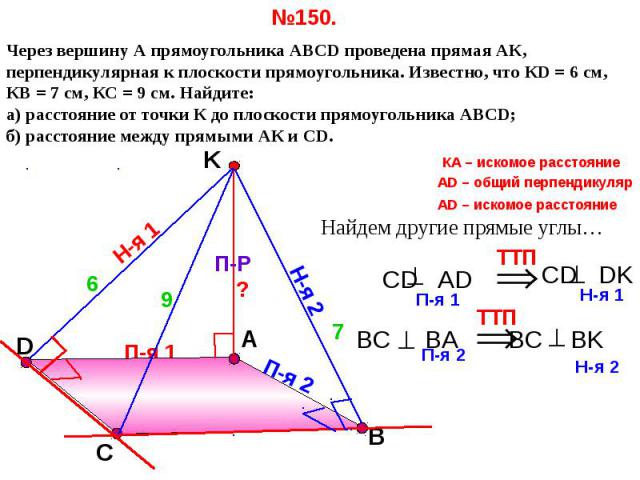
№150. Через вершину А прямоугольника АВСD проведена прямая АК, перпендикулярная к плоскости прямоугольника. Известно, что КD = 6 см, КВ = 7 см, КС = 9 см. Найдите: а) расстояние от точки К до плоскости прямоугольника АВСD; б) расстояние между прямыми АК и СD.

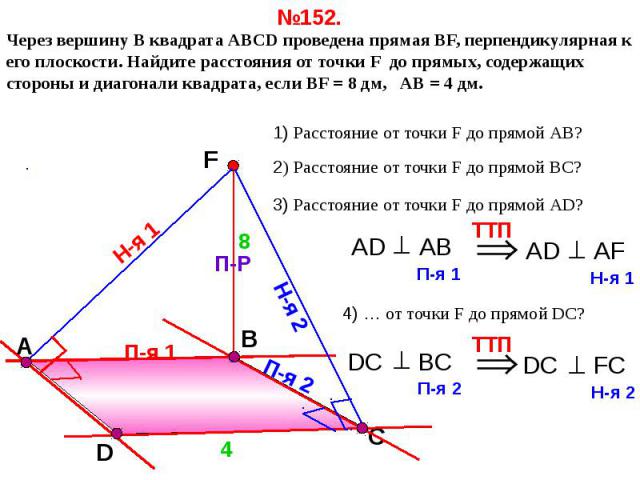
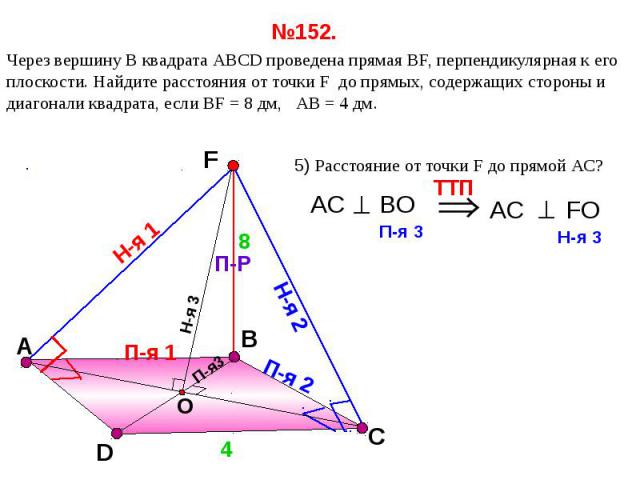
№152. Через вершину B квадрата АВСD проведена прямая ВF, перпендикулярная к его плоскости. Найдите расстояния от точки F до прямых, содержащих стороны и диагонали квадрата, если ВF = 8 дм, АВ = 4 дм. 1) Расстояние от точки F до прямой АВ?2) Расстояние от точки F до прямой ВС?3) Расстояние от точки F до прямой АD?
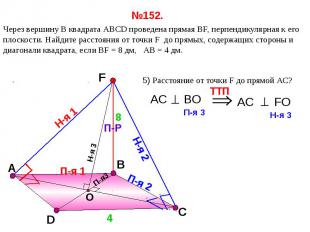
№152. Через вершину B квадрата АВСD проведена прямая ВF, перпендикулярная к его плоскости. Найдите расстояния от точки F до прямых, содержащих стороны и диагонали квадрата, если ВF = 8 дм, АВ = 4 дм.
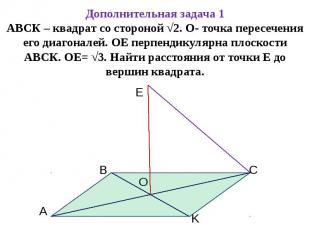
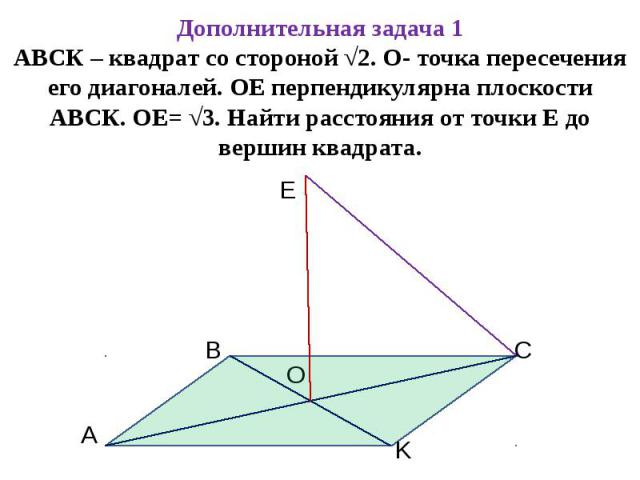
Дополнительная задача 1АВСК – квадрат со стороной √2. О- точка пересечения его диагоналей. ОЕ перпендикулярна плоскости АВСК. ОЕ= √3. Найти расстояния от точки Е до вершин квадрата.
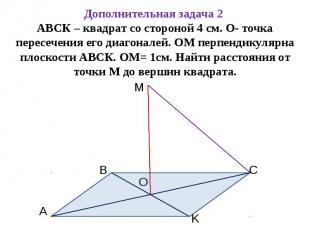
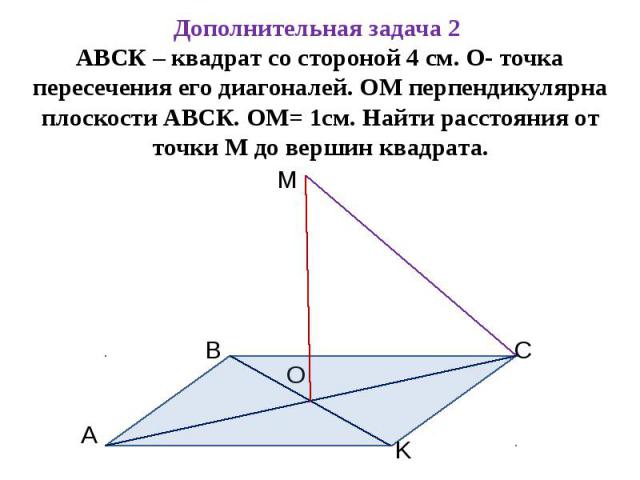
Дополнительная задача 2 АВСК – квадрат со стороной 4 см. О- точка пересечения его диагоналей. ОМ перпендикулярна плоскости АВСК. ОМ= 1см. Найти расстояния от точки М до вершин квадрата.