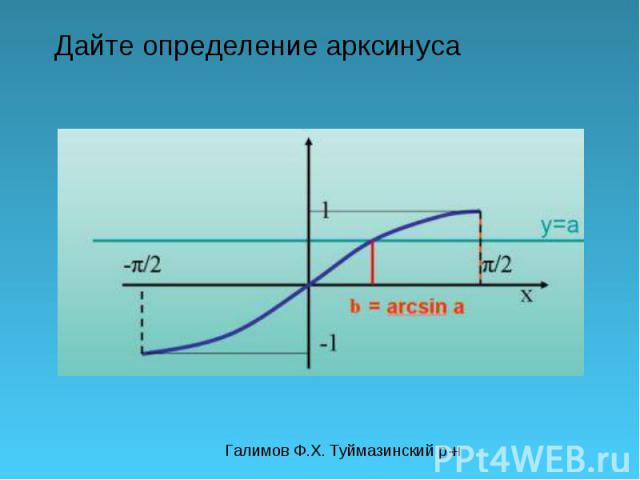
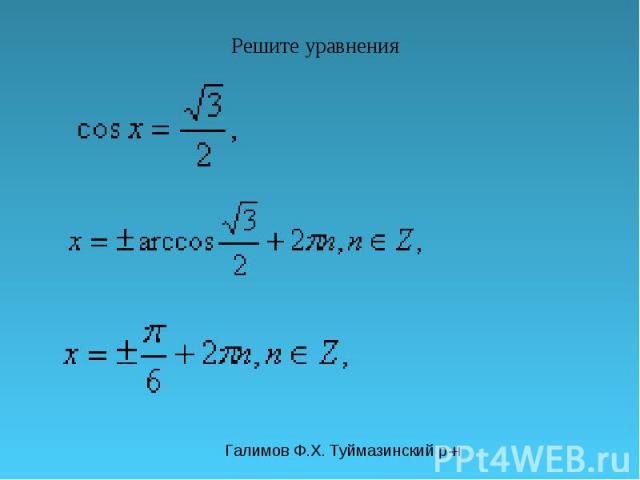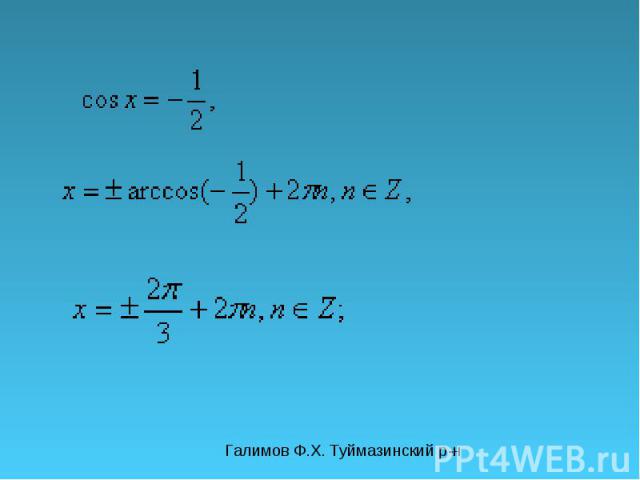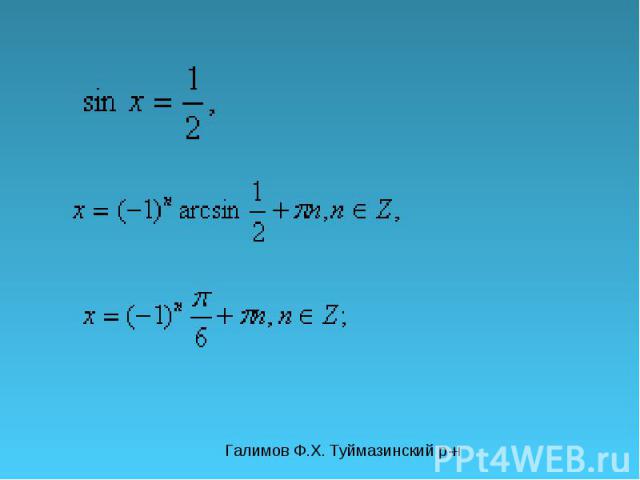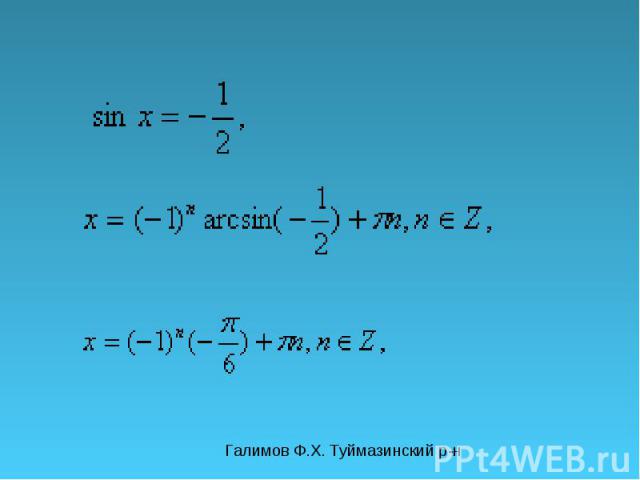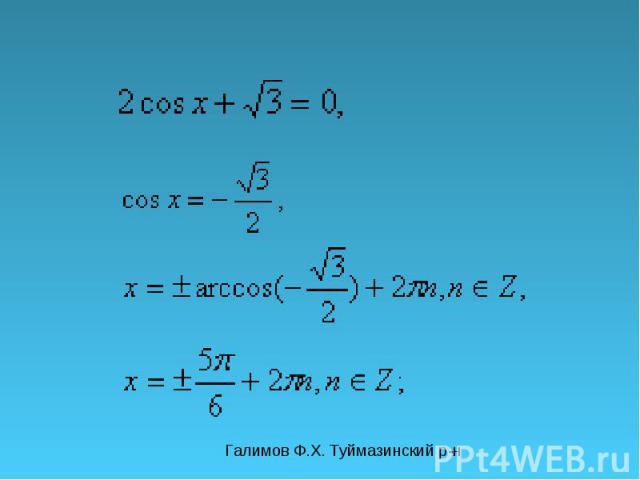Презентация на тему: Дайте определение арксинуса
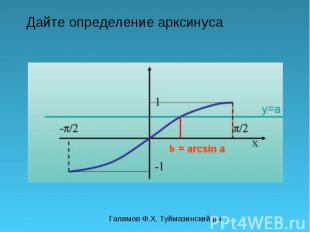
Галимов Ф.Х. Туймазинский р-н Дайте определение арксинуса
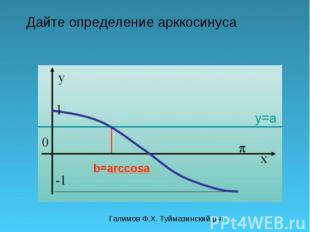
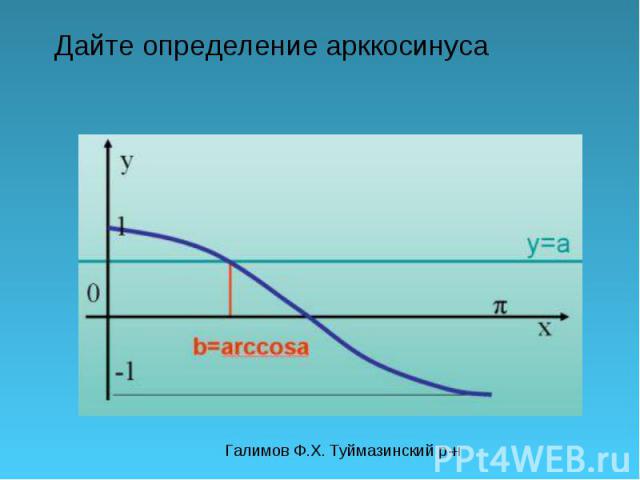
Галимов Ф.Х. Туймазинский р-н Дайте определение арккосинуса
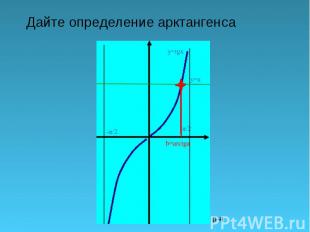
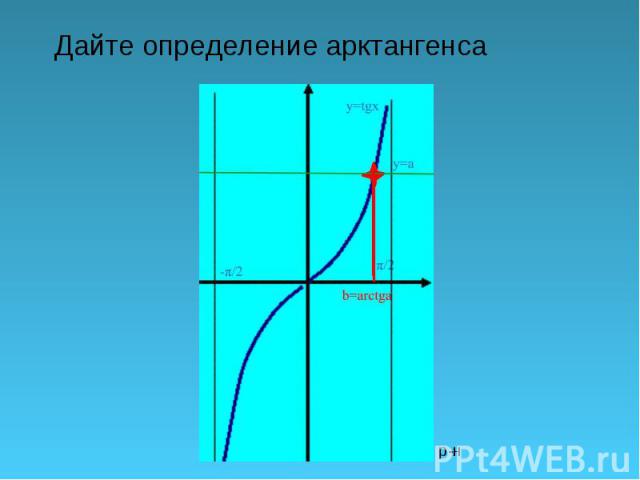
Галимов Ф.Х. Туймазинский р-н Дайте определение арктангенса
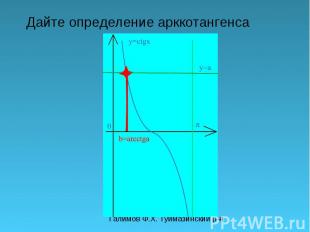
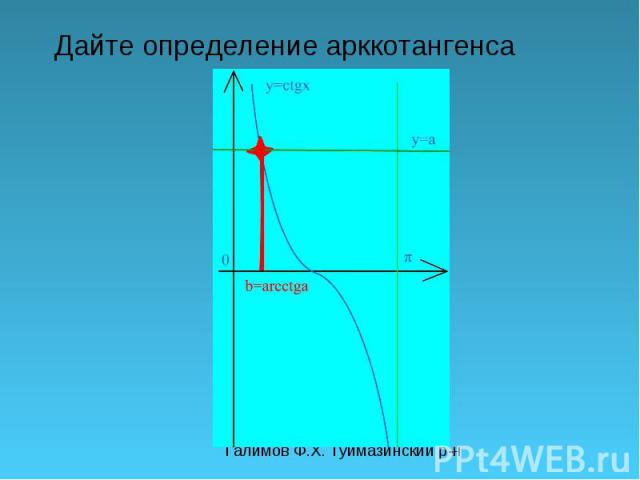
Галимов Ф.Х. Туймазинский р-н Дайте определение арккотангенса
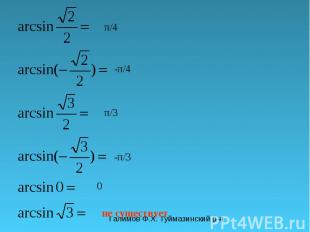
Галимов Ф.Х. Туймазинский р-н π/4 -π/4 π/3 -π/3 0 не существует

Галимов Ф.Х. Туймазинский р-н π/4 3π/4 π/6 5π/6 не существует π/2
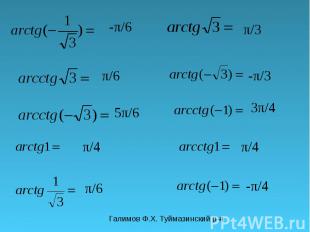
Галимов Ф.Х. Туймазинский р-н -π/6 π/6 5π/6 π/4 π/3 3π/4 π/4 -π/4 π/6 -π/3

Галимов Ф.Х. Туймазинский р-н Имеют ли смысл выражения? Почему?

Галимов Ф.Х. Туймазинский р-н Новая тема. Решение простейших тригонометрических уравнений
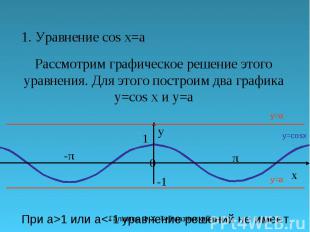
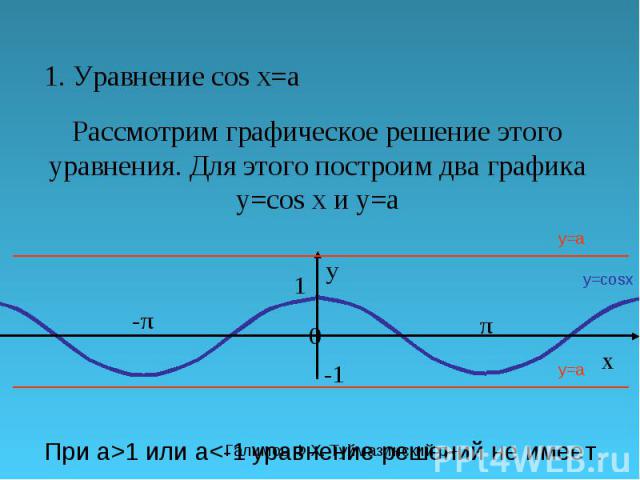
Галимов Ф.Х. Туймазинский р-н 1. Уравнение cos x=a Рассмотрим графическое решение этого уравнения. Для этого построим два графика y=cos x и y=a π y 0 x 1 -π-π y=cosx y=a При а>1 или a
![Галимов Ф.Х. Туймазинский р-н π y 0 x 1 -π-π y=a y=a При aЄ[-1;1] уравнение cos Галимов Ф.Х. Туймазинский р-н π y 0 x 1 -π-π y=a y=a При aЄ[-1;1] уравнение cos](https://fs1.ppt4web.ru/images/3018/82690/310/img10.jpg)
Галимов Ф.Х. Туймазинский р-н π y 0 x 1 -π-π y=a y=a При aЄ[-1;1] уравнение cos x=a имеет бесконечное множество решений. Мы можем записать одно из решений для х Є[0; π]. x 1 =arccos a Другие решения выразим через это решение. x 2 =-arccos a x 3 =arccos a-2π -2π +2π x 4 =-arccos a+2π Функция y=cos x имеет период 2π, поэтому остальные решения отличаются от х 1 и х 2 на 2πn, где nЄZ. Таким образом все решения уравнения cos x=a записываются в виде x=±arccos a+2 πn, nЄZ
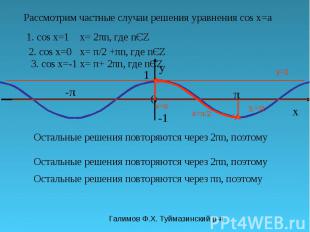
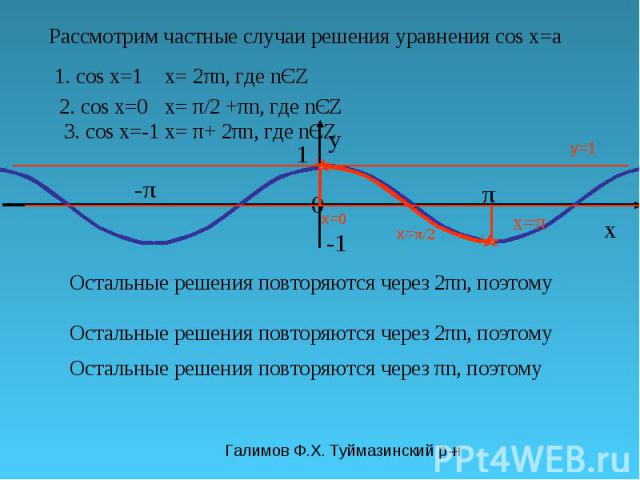
Галимов Ф.Х. Туймазинский р-н π y 0 x 1 -π-π y=1 Рассмотрим частные случаи решения уравнения cos x=a 1. cos x=1 x= π/2 Остальные решения повторяются через 2πn, поэтому x= 2πn, где nЄZ 2. cos x=0 x= 0 Остальные решения повторяются через πn, поэтому x= π/2 +πn, где nЄZ 3. cos x=-1 Остальные решения повторяются через 2πn, поэтому x= π+ 2πn, где nЄZ x=π
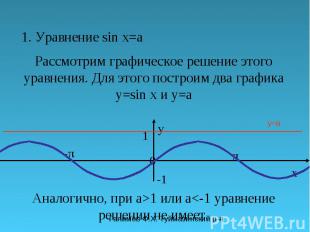
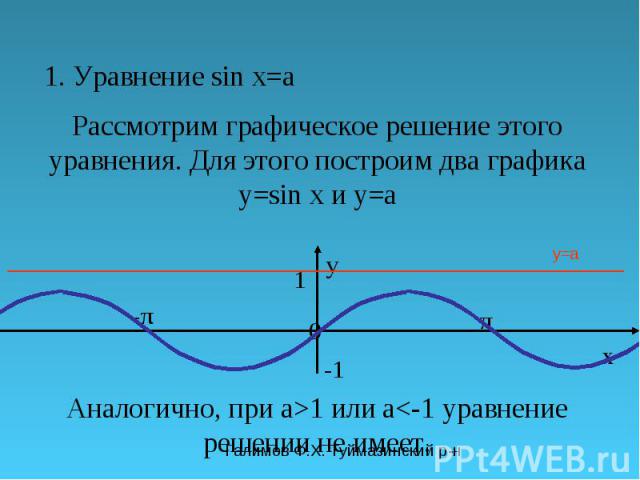
Галимов Ф.Х. Туймазинский р-н 1. Уравнение sin x=a Рассмотрим графическое решение этого уравнения. Для этого построим два графика y=sin x и y=a π y 0 x 1 -π-π y=a Аналогично, при a>1 или a
![Галимов Ф.Х. Туймазинский р-н π y 0 x 1 -π-π y=a При aЄ[-1;1] уравнение sin x=a Галимов Ф.Х. Туймазинский р-н π y 0 x 1 -π-π y=a При aЄ[-1;1] уравнение sin x=a](https://fs1.ppt4web.ru/images/3018/82690/310/img13.jpg)
Галимов Ф.Х. Туймазинский р-н π y 0 x 1 -π-π y=a При aЄ[-1;1] уравнение sin x=a имеет бесконечное множество решений. Мы можем записать одно из решений для х Є[- π/2; π/2]. x 1 =arcsin a Другие решения выразим через это решение. x 2 = π- arcsin a Так-как функция y=sin x имеет период 2π, остальные решения отличаются от этих двух на 2πn, где nЄZ. Получаем две группы решении x 1 =arcsin a+ 2πn, x 2 = π -arcsin a+ 2πn, где nЄZ,

Галимов Ф.Х. Туймазинский р-н Получаем две группы решении x 1 =arcsin a+ 2πn, x 2 = π -arcsin a+ 2πn, где nЄZ. Эти две группы можно записать одной формулой x=(-1) n arcsin a+ πn, где nЄZ
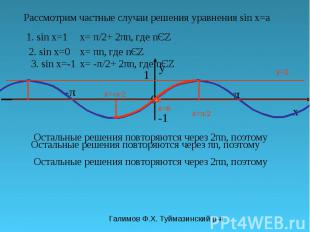
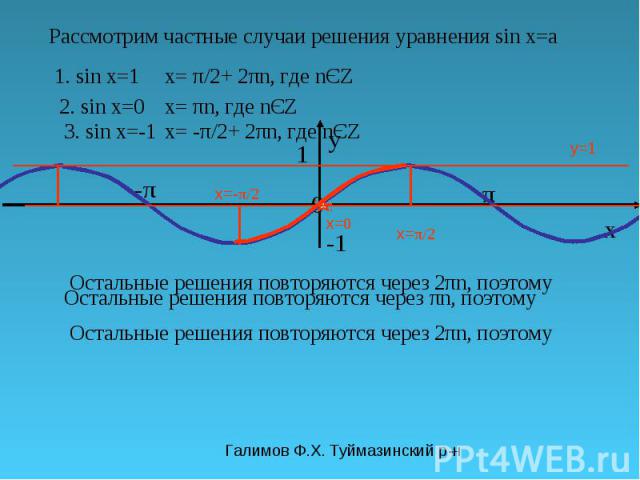
Галимов Ф.Х. Туймазинский р-н π y 0 x 1 -π-π y=1 Рассмотрим частные случаи решения уравнения sin x=a 1. sin x=1 x= π/2 Остальные решения повторяются через 2πn, поэтому x= π/2+ 2πn, где nЄZ 2. sin x=0 x= 0 Остальные решения повторяются через πn, поэтому x= πn, где nЄZ 3. sin x=-1 Остальные решения повторяются через 2πn, поэтому x= -π/2+ 2πn, где nЄZ x=- π/2

Галимов Ф.Х. Туймазинский р-н Решите уравнения
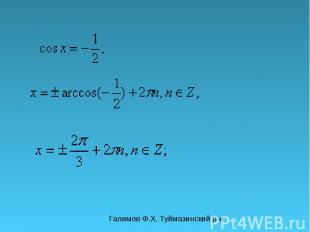
Галимов Ф.Х. Туймазинский р-н

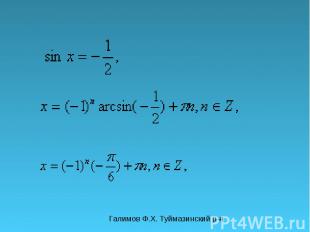
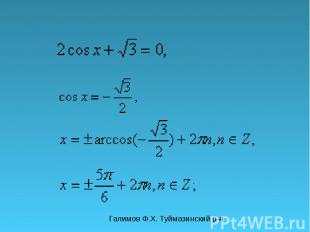
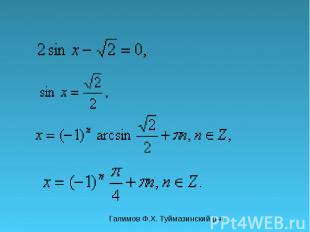

С решением уравнении tg x=a и ctg x=a попробуйте разобраться самостоятельно. Для этого в папке урок2 откройте веб страницу index и следуйте инструкциям. Д/р:п.9, 136(в,г), 137(в,г), 138(в,г), 139(в,г).

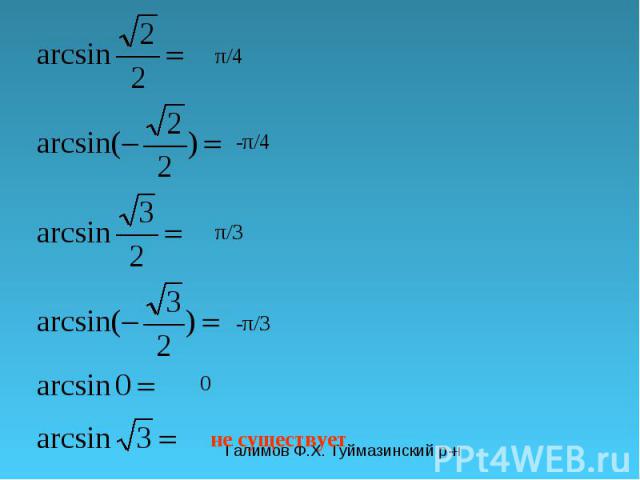

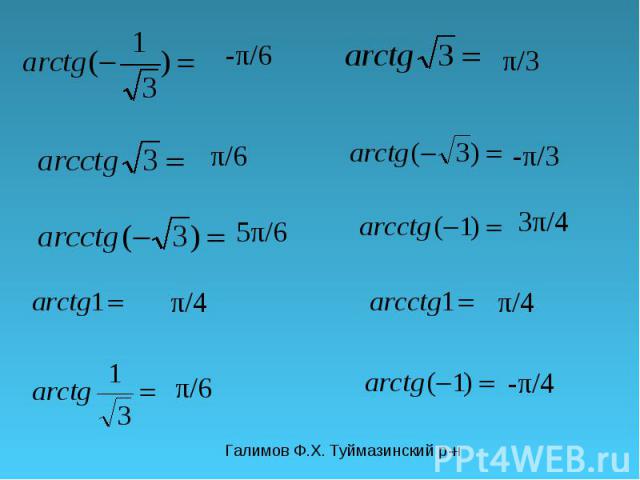


![Галимов Ф.Х. Туймазинский р-н π y 0 x 1 -π-π y=a y=a При aЄ[-1;1] уравнение cos x=a имеет бесконечное множество решений. Мы можем записать одно из решений для х Є[0; π]. x 1 =arccos a Другие решения выразим через это решение. x 2 =-arccos a x 3 =arc… Галимов Ф.Х. Туймазинский р-н π y 0 x 1 -π-π y=a y=a При aЄ[-1;1] уравнение cos x=a имеет бесконечное множество решений. Мы можем записать одно из решений для х Є[0; π]. x 1 =arccos a Другие решения выразим через это решение. x 2 =-arccos a x 3 =arc…](https://fs1.ppt4web.ru/images/3018/82690/640/img10.jpg)
![Галимов Ф.Х. Туймазинский р-н π y 0 x 1 -π-π y=a При aЄ[-1;1] уравнение sin x=a имеет бесконечное множество решений. Мы можем записать одно из решений для х Є[- π/2; π/2]. x 1 =arcsin a Другие решения выразим через это решение. x 2 = π- arcsin a Так… Галимов Ф.Х. Туймазинский р-н π y 0 x 1 -π-π y=a При aЄ[-1;1] уравнение sin x=a имеет бесконечное множество решений. Мы можем записать одно из решений для х Є[- π/2; π/2]. x 1 =arcsin a Другие решения выразим через это решение. x 2 = π- arcsin a Так…](https://fs1.ppt4web.ru/images/3018/82690/640/img13.jpg)