Презентация на тему: Площади фигур геометрия

Площади фигур. Материал к уроку геометрии в 8 классе. Авторы: Зырянова Н. Джафарова А 8б класс Учитель: Ивниаминова Л.А. 900igr.net

Площадь- это.. Квадратный сантиметр- это площадь квадрата со стороной 1 см.. Что бы найти площадь фигуры надо определить, сколько таких квадратов в данной фигуре укладывается. Равные – если при наложении они совпадут. Равные фигуры имеют равные площади. Фигуры имеющие равные площади называются равновеликими. Площадь всей фигуры, разделенной на части равна сумме площадей этих частей.

Прямоугольник, треугольник, параллелограмм. а b D A B C b a S=a×b S=AD*BH b a S=(a×b):2 H

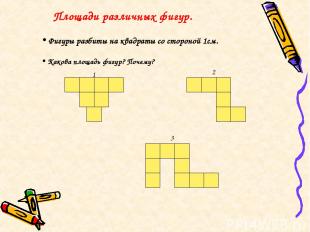
Площади различных фигур. 1 2 3 Фигуры разбиты на квадраты со стороной 1см. Какова площадь фигур? Почему?

Единицы измерения площадей. Квадратный миллиметр. Квадратный сантиметр. Гектар.(1га=10 000м²) Ар.(1а=100м²)

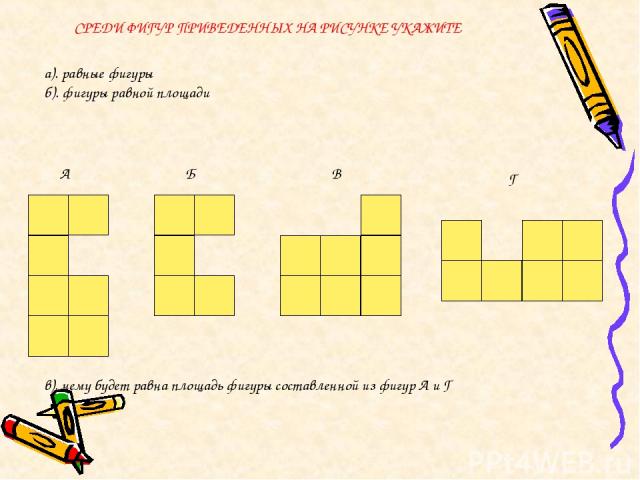
СРЕДИ ФИГУР ПРИВЕДЕННЫХ НА РИСУНКЕ УКАЖИТЕ а). равные фигуры б). фигуры равной площади в). чему будет равна площадь фигуры составленной из фигур А и Г А Б В Г

Решите ребус П ``` `` `````` ь

ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА РАВНА ПРОИЗВЕДЕНИЮ ЕГО СМЕЖНЫХ СТОРОН Дано: Доказать: ABCD-прямоугольник S=ab AB=b AD=a SABCD=S Доказательство: 1) Достроим прямоугольник до квадрата со стороной (a+b) 2) По свойству 3 Sкв. = (a+b)2 3) По свойству 2 имеем SКВ =S + S + a2 + b2 S = ab 4) По свойству 1 имеем: (a+b)2 = S + S + a2 + b2 а2 + 2ab + b2 = 2S + a2 + b2 2S = 2ab S=a2 S S=b2 S a a a a a b b b b A B C D

Площадь параллелограмма Дано: ABCD-параллелограмм Доказать: S=AD*BH Доказательство: трапеция ABCK составлена из параллелограмма и треугольника DCK. С другой стороны, она составлена из прямоугольника HBCK и треугольника ABH. Прямоугольные треуг. DCK и ABH равны (по гипотенузе и острому углу), поэтому их площади равны => Площади ABCD и HBCK также равны,т.е. площадь прямоугольника HBCK равна S. По теореме => S=BC*BH,а так как BC=AD,то S=AD*BH А В С D H K 1 2

Площадь треугольника Дано: АСВ-треугольник S-площадь Доказать: S=1/2AB*CH Доказательство: Достроим треугольник ACB до параллелограмма ABDC. Треугольники ABC и DCB равны по трём сторонам =>площадь реугольника АВС равна половине площади параллелограмма BDC, т.е. S=1/2AB*CH. A C B H D

Теорема Пифагора. Дано: Прямоугольный треугольник a, b-катеты, c-гипотенуза Доказать: c2 = a2 + b2 Доказательство: Достроим треугольник до квадрата со стороной a + b. Площадь квадрата равна (a + b)2. C другой стороны, этот квадрат составлен из 4х прямоугольных треугольников, площадь каждого равна 1/2ab, и квадрата со стороной с=> S = 4∙1/2ab+c2=2ab+c2. Таким образом, (a+b)2 = 2ab+c2,откуда c2=a2+b2 а b a b c c

Л.С.Атанасян, В.Ф.Бутузов и другие, Геометрия: учебник для 7-9 классов А.В.Погорелов, Геометрия: учебник для 7-11 классов

Спасибо за внимание!