Презентация на тему: Расстояние между скрещивающимися прямыми

Нахождение расстояния между скрещивающимися прямыми С2

Материал, полученный и собранный в ходе работы над проектом, является незаменимым при подготовке к решению задач ЕГЭ С2. Умение решать задачи на нахождение расстояния между скрещивающимися прямыми разными способами может существенно сократить время их решения. С2

Способы нахождения: 1) Общий перпендикуляр – отрезок, перпендикулярный 2м параллельным плоскостям, в которых лежат скрещ. прямые. 2)Перпендикуляр между прямой и проекцией другой прямой. Первая прямая лежит в плоскости, а другая пересекает её под прямым углом 3)Перпендикуляр между прямыми. Одна прямая лежит в плоскости, а другая параллельна этой плоскости 4)Перпендикуляр между проекциями на плоскость.

Построение общего перпендикуляра. II способ

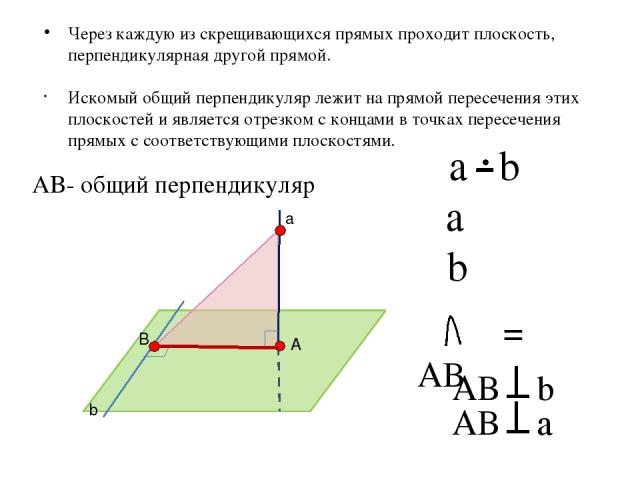
Искомый общий перпендикуляр лежит на прямой пересечения этих плоскостей и является отрезком с концами в точках пересечения прямых с соответствующими плоскостями. а b A B α β a ϵ α b ϵ β α β = AB AB b AB a AB- общий перпендикуляр Через каждую из скрещивающихся прямых проходит плоскость, перпендикулярная другой прямой. a b

Другой вариант построения

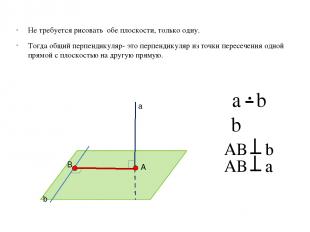
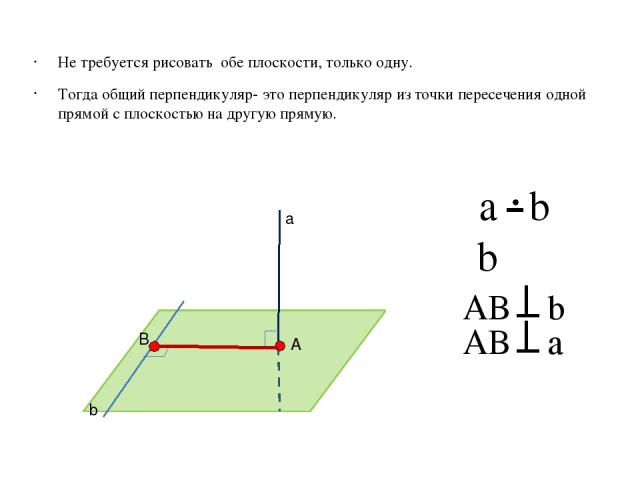
Не требуется рисовать обе плоскости, только одну. Тогда общий перпендикуляр- это перпендикуляр из точки пересечения одной прямой с плоскостью на другую прямую. AB b b ϵβ AB a а b β A B a b

Задача №1

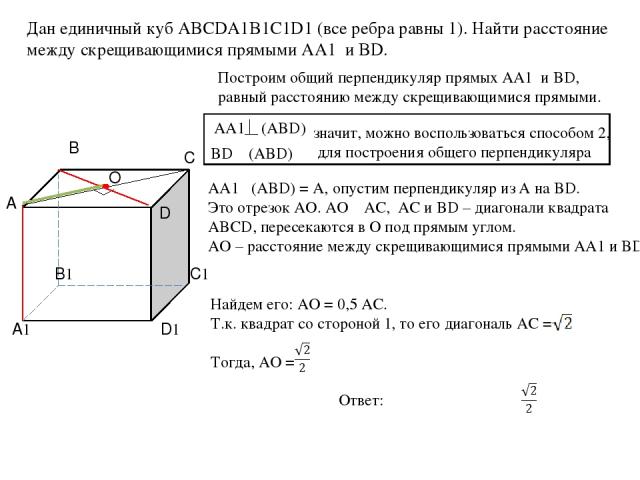
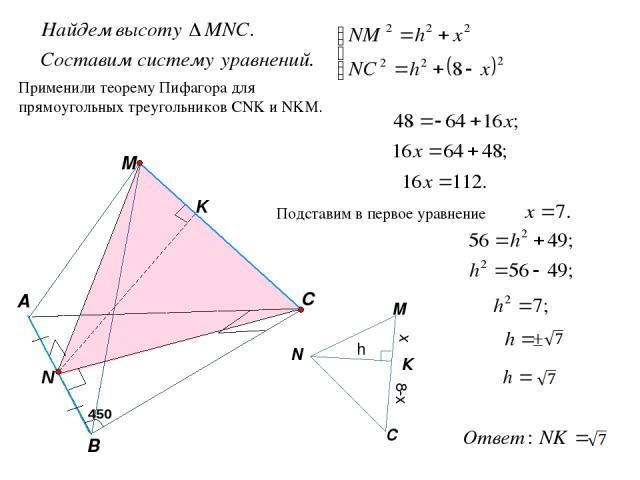
AA1 (АBD) Дан единичный куб ABCDA1B1C1D1 (все ребра равны 1). Найти расстояние между скрещивающимися прямыми AA1 и BD. Построим общий перпендикуляр прямых AA1 и BD, равный расстоянию между скрещивающимися прямыми. BD ϵ (ABD) значит, можно воспользоваться способом 2, для построения общего перпендикуляра AA1 (ABD) = A, опустим перпендикуляр из А на BD. Это отрезок АО. АО ϵ АС, АС и BD – диагонали квадрата ABCD, пересекаются в О под прямым углом. АО – расстояние между скрещивающимися прямыми AA1 и BD Найдем его: АО = 0,5 АС. Т.к. квадрат со стороной 1, то его диагональ АС = Тогда, АО = Ответ: A B C D O A1 B1 C1 D1

Задача №2

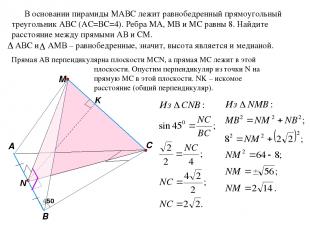
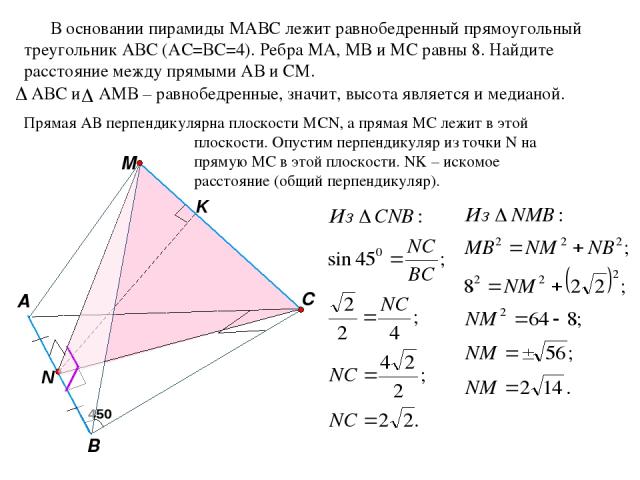
M C A B В основании пирамиды MАВС лежит равнобедренный прямоугольный треугольник АВС (АС=ВС=4). Ребра МА, МВ и МС равны 8. Найдите расстояние между прямыми АВ и СМ. Прямая АВ перпендикулярна плоскости MCN, а прямая МС лежит в этой плоскости. Опустим перпендикуляр из точки N на прямую МС в этой плоскости. NK – искомое расстояние (общий перпендикуляр). 450 АВС и AМВ – равнобедренные, значит, высота является и медианой. K NK – общий перпендикуляр. NK перпендикулярно MC по построению. MK перпендикулярен к ребру АВ, т.к. МК перпендикулярен к плоскости MCN, значит он будет перпендикулярен любой прямой, лежащей в этой плоскости.

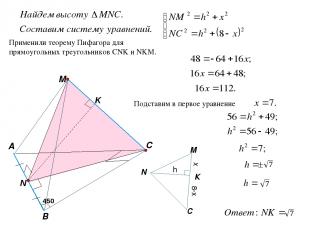
M C A B Применили теорему Пифагора для прямоугольных треугольников СNK и NKM. Подставим в первое уравнение М N C h x 8-x К 450 K