Презентация на тему: Применение подобия к доказательству теорем и решению задач

Применение подобия к доказательству теорем и решению задач

Цели урока:Ввести определение средней линии треугольника.Сформулировать и доказать теорему о средней линии треугольника.Рассмотреть решение задач на применение доказанной теоремы.Рассмотреть решение задачи о свойстве медиан треугольника.

Ход урока Решение задач по готовым чертежам.Изучение нового материала.Закрепление изученной темы.Итоги урокаДомашнее задание
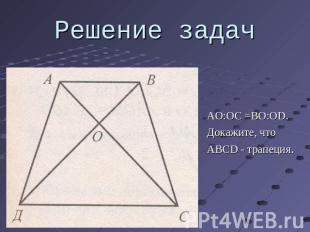
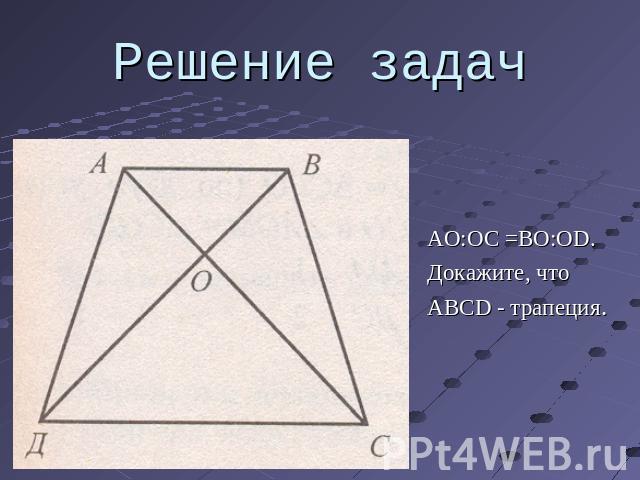
Решение задач AO:OC =BO:OD.Докажите, чтоABCD - трапеция.
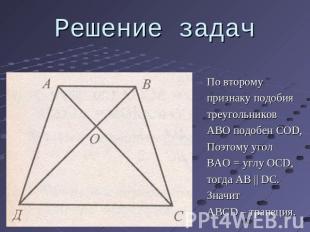
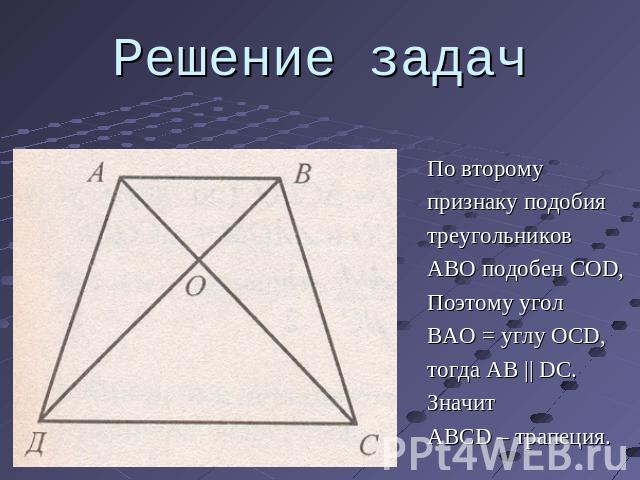
Решение задач По второмупризнаку подобиятреугольниковABO подобен COD,Поэтому угол BAO = углу OCD,тогда AB || DС.ЗначитABCD – трапеция.
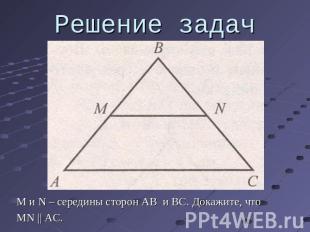
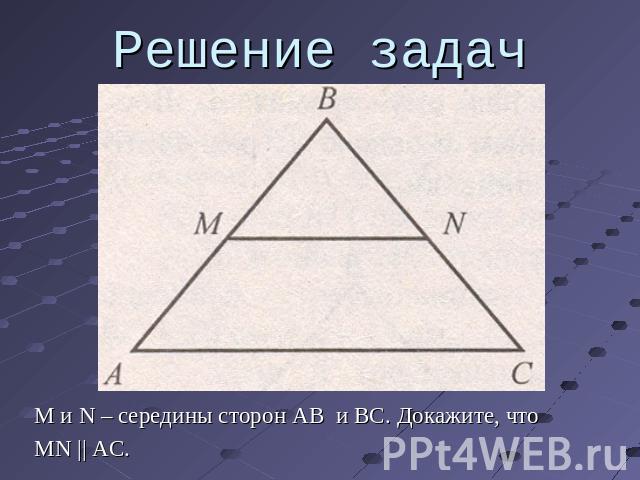
Решение задач М и N – середины сторон AB и BC. Докажите, чтоMN || AC.

Решение задач По второму признаку подобия треугольников ABCподобен MBN, поэтому угол BMN = углу ABC, а значитMN||AC.

Объяснение нового материала Определение средней линии треугольника.Теорема о средней линии треугольника.

Закрепление изученного материала № 564 (устно)№ 567№ 1№ 570
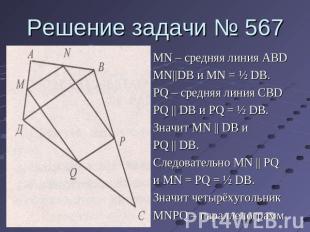
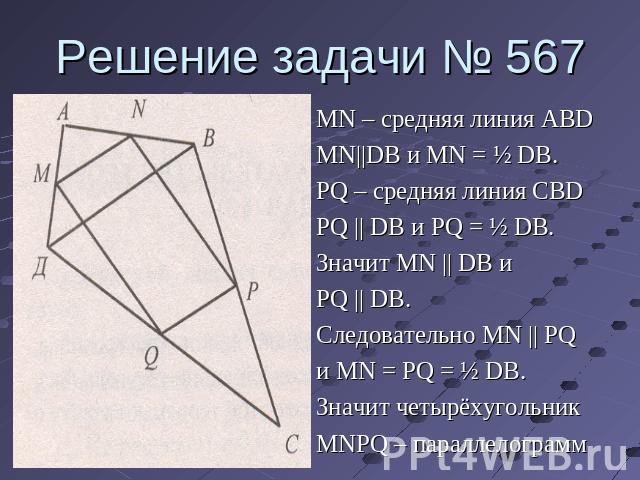
Решение задачи № 567 MN – средняя линия ABDMN||DB и MN = ½ DB.PQ – средняя линия CBDPQ || DB и PQ = ½ DB.Значит MN || DB иPQ || DB.Следовательно MN || PQи MN = PQ = ½ DB.Значит четырёхугольникMNPQ – параллелограмм
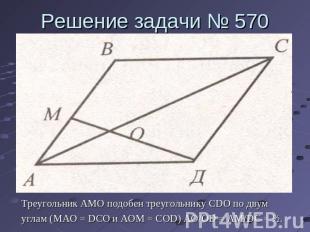
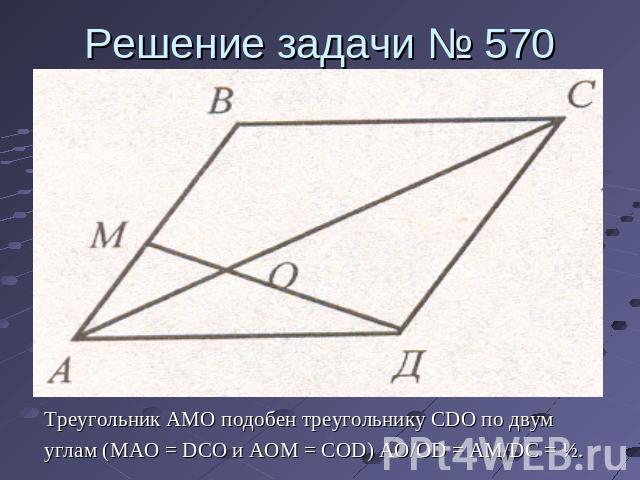
Решение задачи № 570 Треугольник AMO подобен треугольнику CDO по двумуглам (MAO = DCO и AOM = COD) AO/OD = AM/DC = ½.
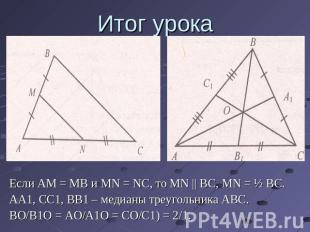
Итог урока Если AM = MB и MN = NC, то MN || BC, MN = ½ BC.AA1, CC1, BB1 – медианы треугольника ABC.BO/B1O = AO/A1O = CO/C1) = 2/1.

Домашнее задание Вопросы стр. 154: 8, 9.№ 565№ 566№ 571

Литература Л. С. Атанасян и другие «Геометрия»Учебник для 7 – 9 классов. Москва просвещение 2002гЛ. С. Атанасян и другие «Геометрия» Пробный учебник для 6 – 8 классов., Москва просвещение 1981гЛ. С. Атанасян и другие «Изучение геометрии в 7 – 9 классах.