Презентация на тему: Осевая и центральная симетрия

Осевая и центральная симетрия

Осевая симметрия Две точки А и А1 называются симметричными относительно прямой a, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. А а А1

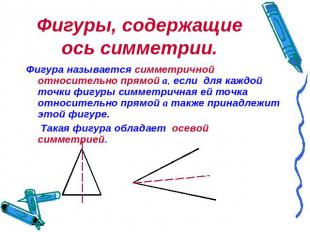
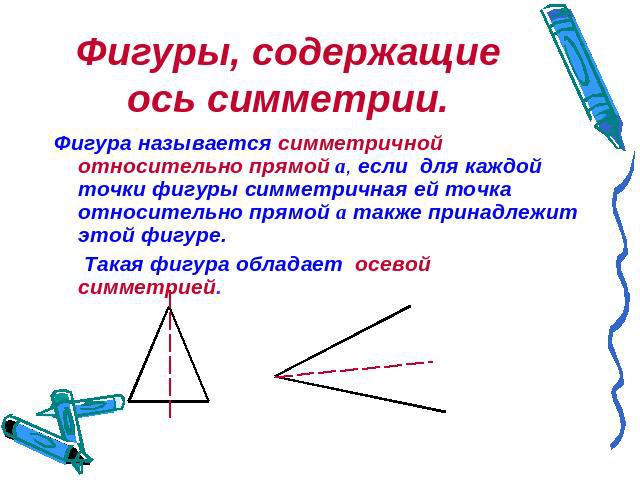
Фигуры, содержащие ось симметрии. Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Такая фигура обладает осевой симметрией.

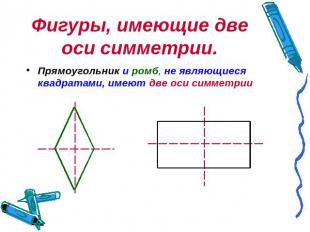
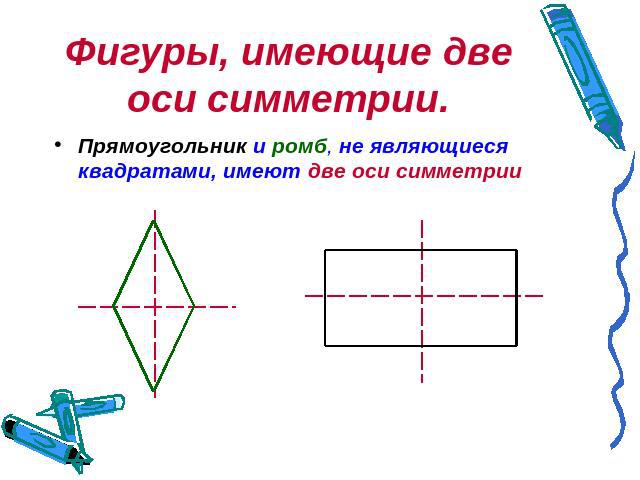
Фигуры, имеющие две оси симметрии. Прямоугольник и ромб, не являющиеся квадратами, имеют две оси симметрии

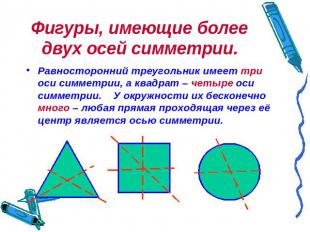
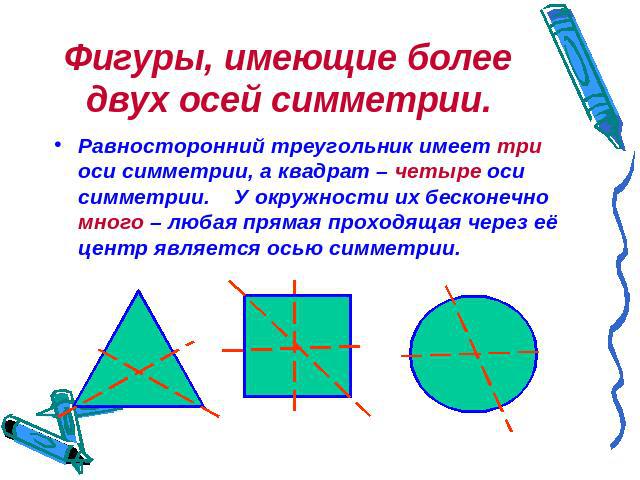
Фигуры, имеющие более двух осей симметрии. Равносторонний треугольник имеет три оси симметрии, а квадрат – четыре оси симметрии. У окружности их бесконечно много – любая прямая проходящая через её центр является осью симметрии.

Фигуры, не имеющие осей симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.

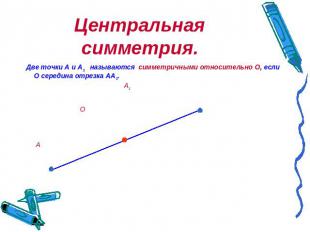
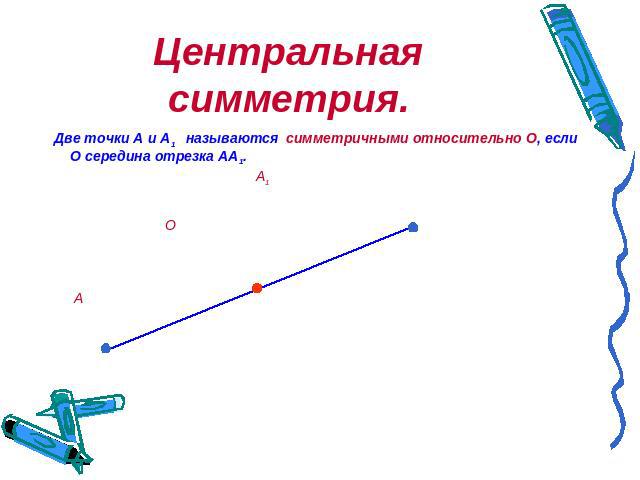
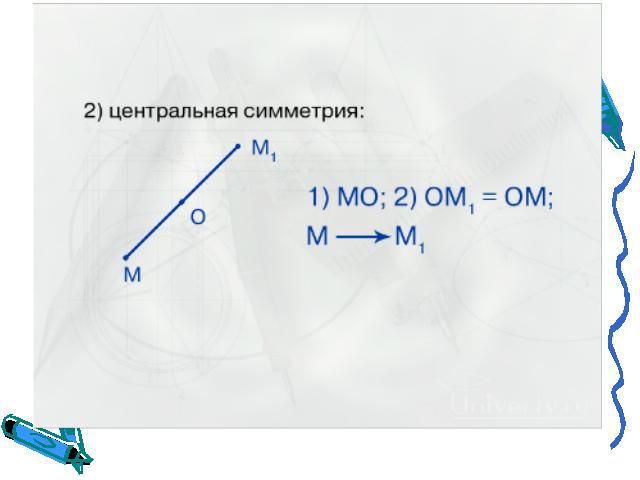
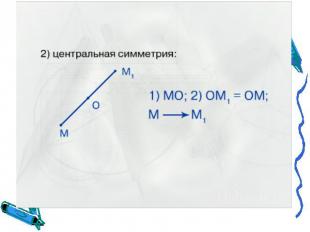
Центральная симметрия. Две точки А и А1 называются симметричными относительно О, если О середина отрезка АА1. А1 О А

Фигура, симметричная, относительно точки. Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии. Такая фигура обладает центральной симметрией. B А О Любая точка прямой является центром симметрии.

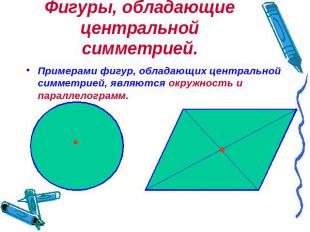
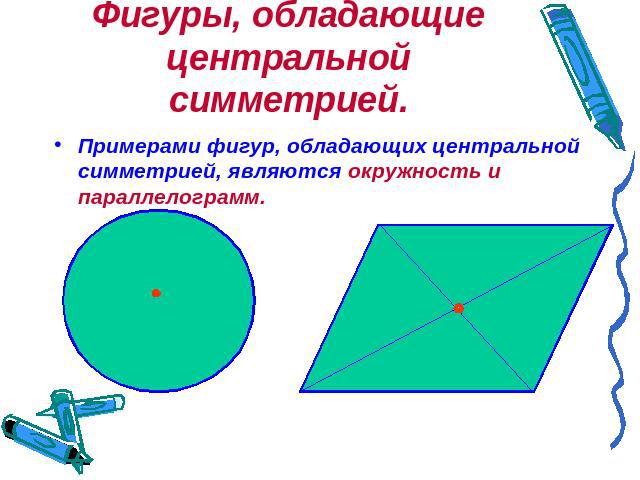
Фигуры, обладающие центральной симметрией. Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм.

Симметрия предметов на плоскости. Изображения предметов на плоскости из окружающего мира имеет ось или центр симметрии. С симметрией мы встречаемся в природе, быту, архитектуре и технике.

Симметрия в быту

Симметрия в науке и технике.

Симметрия в архитектуре

Центральная симметрия Геометрическая фигура ( или тело ) называется симметричной относительно центра C ( рис.105 ), если для каждой точки A этой фигуры может быть найдена точка E этой же фигуры, так что отрезокAE проходит через центр C и делится в этой точке пополам ( AC = CE ). Точка C называется центром симметрии.

Зеркальная симметрия . Геометрическая фигура называется симметричной относительно плоскости S ( рис.104 ), если для каждой точки E этой фигуры может быть найдена точка E’ этой же фигуры, так что отрезок EE’ перпендикулярен плоскости S и делится этой плоскостью пополам ( EA =AE’ ). Плоскость S называется  плоскостью симметрии. Симметричные фигуры, предметы и тела не равны друг другу в узком смысле слова (например, левая перчатка не подходит для правой руки и наоборот ). Они называются зеркально равными.

Симметрия вращения Тело ( фигура ) обладает симметрией вращения ( рис.106 ), если при повороте на угол 360°/n  ( здесь n – целое число ) вокруг некоторой прямой AB ( оси симметрии ) оно полностью совпадает со своимначальным положением. При n = 2 мы имеем  осевую симметрию. 

Примеры вышеупомянутых видов симметрии Шар ( сфера ) обладает и центральной, и зеркальной, и симметрией вращения. Центром симметрии является центр шара; плоскостью симметрии является плоскость любого большого круга; осью симметрии – диаметр шара.Круглый конус обладает осевой симметрией; ось симметрии – ось конуса.Прямая призма обладает зеркальной симметрией. Плоскость симметрии параллельна её основаниям и расположена на одинаковом расстоянии между ними.

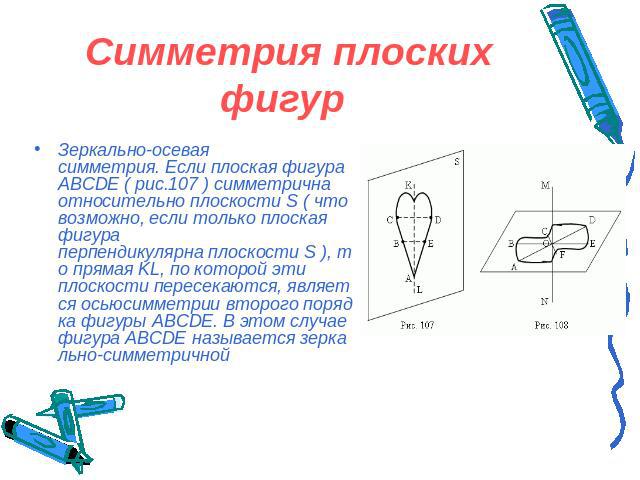
Симметрия плоских фигур Зеркально-осевая симметрия. Если плоская фигура ABCDE ( рис.107 ) симметрична относительно плоскости S ( что возможно, если только плоская фигура перпендикулярна плоскости S ), то прямая KL, по которой эти плоскости пересекаются, является осьюсимметрии второго порядка фигуры ABCDE. В этом случае фигура ABCDE называется зеркально-симметричной

Центральная симметрия. Если плоская фигура ( ABCDEF, рис.108 ) имеет ось симметрии второго порядка, перпендикулярную плоскости фигуры (прямая MN, рис.108 ), то точка O, в которой пересекаются прямая MN и плоскость фигуры ABCDEF, является центром симметрии.

Примеры симметрии плоских фигур Параллелограмм имеет только центральную симметрию. Его центр симметрии – точка пересечения диагоналей.Равнобочная трапеция имеет только осевую симметрию. Её ось симметрии – перпендикуляр, проведенный через середины оснований трапеции.Ромб имеет и центральную, и осевую симметрию. Его ось симметрии – любая из его диагоналей; центр симметрии – точка их пересечения.

Симметрия в природе Симметрия в нашем представлении тесно связана с понятием красоты Представления о красоте и совершенстве родились и упрочились под воздействием окружающей природы еще у наших далеких предков.. Особенно поражали кристаллы правильностью своих пропорций, безукоризненным повторением формы.

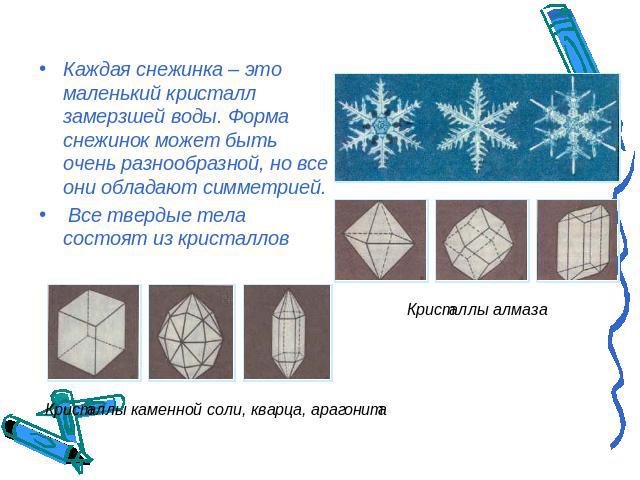
Каждая снежинка – это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией. Все твердые тела состоят из кристаллов

Не только кристаллы, большинство творений природы обычно обладают той или иной формой симметрии. Земля вполне могла бы быть названа царством симметрии. Природа использовала все ее основные виды, которые можно представить по геометрическим соображениям. Подавляющее число живых организмов обладает одной из трех ее видов: шаровидной, лучевой, двусторонняя симметрией.

Симметрия в животном мире

Симметрия в растительном мире

Почему разные организмы обладают разными видами симметрии? Это связано с их образом жизни.

Каждая из изображенных фигур — бабочка, лист растения, дерево — обладает лишь одним видом симметрии, делящей ее на две зеркально равные части. Поэтому данный вид симметрии в биологии называется двусторонней или билатеральной

Спасибо за внимание!! Пригатовила:М Данира 9е клпроверила: Светлана Анатолиевна

конец