Презентация на тему: Закон больших чисел и Центральная предельная теорема

Список литературы 1. Гнеденко б.В. Курс теории вероятностей. – М.: Физматгиз, 1988.2. Ивченко Г.И., Медведев Ю.И. Математическая статистика. 2-е изд. М., 1992.3. Бородин А.Н. Элементарный курс теории вероятностей и математической статистики. 3-е изд., – Спб.: Издательство «лань», 2004 – 256 с.4. Бочаров П.П., Печенкин А.В. Теория вероятностей. Математическая статистика. – М.: Гардарика, 1998. – 328 с.

Список литературы 5. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 2002. – 405 с.6. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие для студентов вузов/ М.: Высшая школа, 2002. – 405 с.

Лекция №1 Закон больших чисел иЦентральная предельная теорема

Неравенство Чебышева

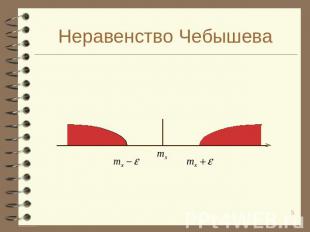
Неравенство Чебышева

Сходимость по вероятности Последовательность случайных величин Сходится по вероятности к величине a если для любых > 0 и > 0 существует такое n( , ), начиная с которого выполняется неравенство: или

Сходимость по вероятности

Графическая иллюстрация сходимости по вероятности

Теорема Чебышева При неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдаемых значений случайной величины, имеющей конечную дисперсию, сходится по вероятности к её математическому ожиданию.

Теорема Чебышева

Обобщенная теорема Чебышева При неограниченном увеличении числа независимых испытаний над случайными величинами, имеющими ограниченные дисперсии, среднее арифметическое наблюдаемых значений сходится по вероятности к среднему арифметическому математических ожиданий эти величин.

Обобщенная теорема Чебышева

Теорема Бернулли При неограниченном увеличении числанезависимых опытов в постоянных условиях частотарассматриваемого события А сходится по вероятности к его вероятности p в отдельном испытании.

Индикатор События И Его Свойства Индикатор события – это случайная величина, принимающая значение, равное единице, если событие произошло и равное нулю – в противном случае.

Ряд распределения Индикатора События Математическое ожидание и дисперсия индикатора

Теорема Пуассона При неограниченном увеличении числа независимых испытаний в переменных условиях частота события сходится по вероятности к среднему арифметическому его вероятностей при данных испытаниях

Центральная Предельная Теорема Рассматривается вопрос о законе распределения суммы случайных величин, когда число слагаемых неограниченно возрастает

Теорема Ляпунова Если случайные величинывзаимно независимы и имеют один и тот же закон распределения с математическим ожиданием m и дисперсией 2, причем существует ограниченный третий абсолютный момент 3 то при неограниченном увеличении n закон распределения суммы приближается к нормальному.

Пример Складываются 24 независимых случайных величины, имеющих равномерное распределение на интервале (0, 1). Написать приближенное выражение для плотности распределения суммы этих случайных величин. Найти вероятность того, что сумма будет заключена в пределах от 6 до 8.