Презентация на тему: Решение простейших тригонометрических уравнений
![Арксинусом числа а называют такое число из отрезка [- П/2; П/2], синус которого Арксинусом числа а называют такое число из отрезка [- П/2; П/2], синус которого](https://fs3.ppt4web.ru/images/133572/193763/310/img0.jpg)
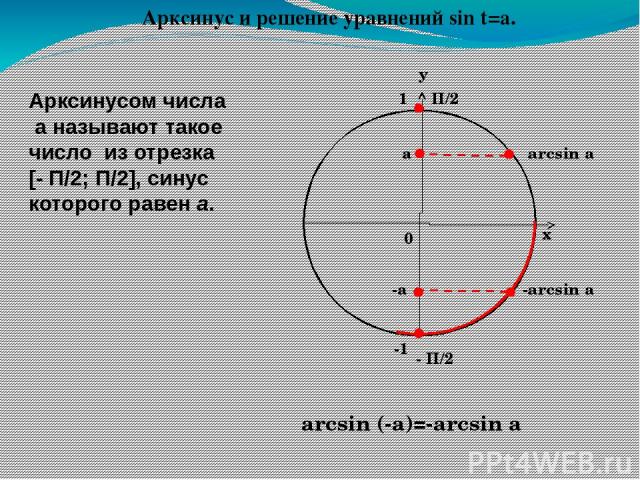
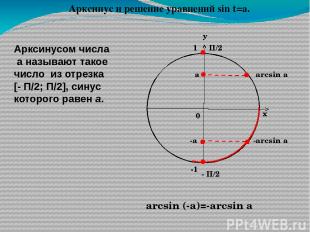
Арксинусом числа а называют такое число из отрезка [- П/2; П/2], синус которого равен а. arcsin а П/2 - П/2 а arcsin (-a)=-arcsin a -а -arcsin а Арксинус и решение уравнений sin t=a. у х 0 1 -1
![П 0 arccos а Арккосинусом числа а называют такое число из промежутка [0;П ], кос П 0 arccos а Арккосинусом числа а называют такое число из промежутка [0;П ], кос](https://fs3.ppt4web.ru/images/133572/193763/310/img1.jpg)
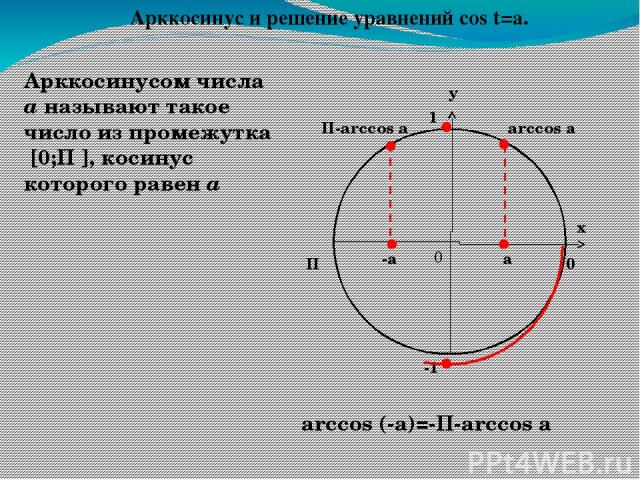
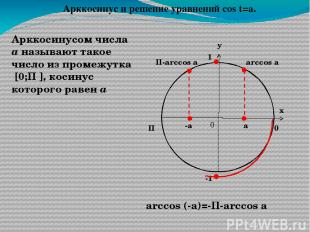
П 0 arccos а Арккосинусом числа а называют такое число из промежутка [0;П ], косинус которого равен а а arccos (-a)=-П-arccos a -а П-arccos a Арккосинус и решение уравнений соs t=a. у х 0 1 -1

Цели урока: Образовательные: Актуализировать знания учащихся по теме «Решение простейших тригонометрических уравнений» и обеспечить их применение при решении задач; Повторить, углубить, обобщить и систематизировать приобретенные знания по теме «Обратные тригонометрические уравнения» для дальнейшего использования при решении тригонометрических уравнений.

Развивающие: Содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать; Формировать и развивать общеучебные умения и навыки: обобщение, поиск способов решения; Отрабатывать навыки самооценивания знаний и умений, выбора задания, соответствующего их уровню развития.

Воспитательные: Вырабатывать внимание, самостоятельность при работе на уроке; Способствовать формированию активности и настойчивости, максимальной работоспособности; Развивать интерес к урокам математики.
Обратные тригонометрические функции у=arcsinx у=arccosx у=arctgx у=arcctgx
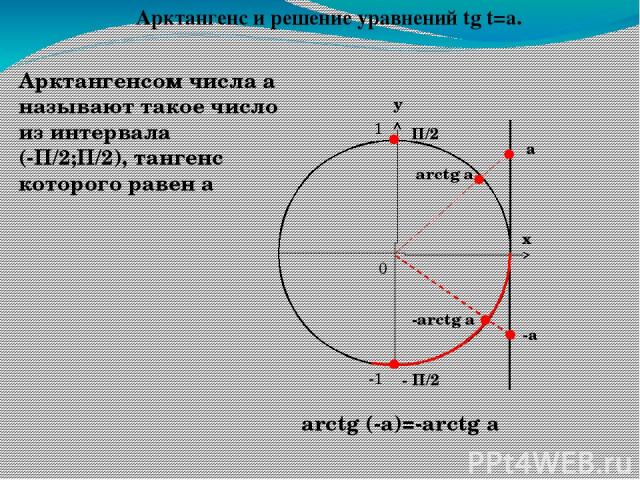
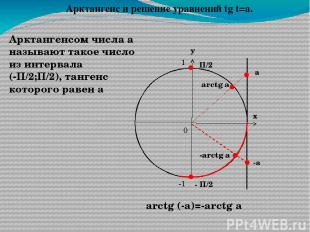
Арктангенсом числа а называют такое число из интервала (-П/2;П/2), тангенс которого равен а arctg a а П/2 - П/2 arctg (-a)=-arctg a -а -arctg a Арктангенс и решение уравнений tg t=a. у х 0 1 -1
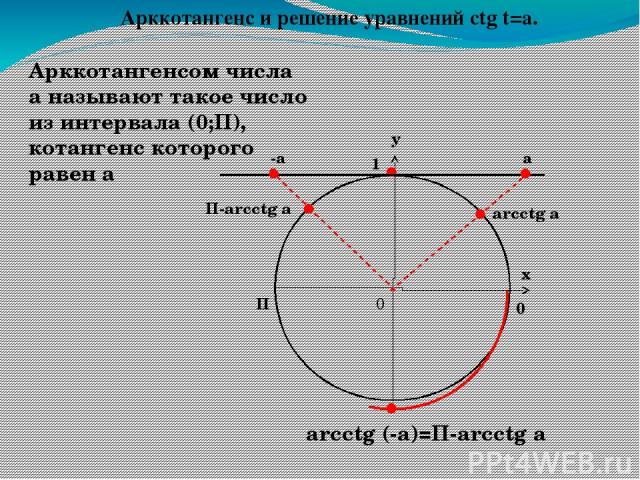
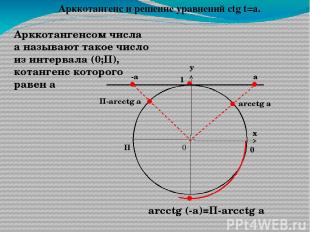
у х 0 1 П 0 Арккотангенсом числа а называют такое число из интервала (0;П), котангенс которого равен а -а arcctg a arcctg (-a)=П-arcсtg a а П-arcctg a Арккотангенс и решение уравнений сtg t=a.
Определение Уравнения с неизвестной переменной, заданной в виде аргумента тригонометрической функции, называется тригонометрическим уравнением. Решить тригонометрическое уравнение – значит найти значения аргумента, приводящие данное уравнение в верное тождество. Простейшими тригонометрическими уравнениями называют уравнения вида cos x=a, sin x=a, tg x= a, ctg x=a. В этих уравнениях переменная находится под знаком тригонометрической функции, а – данное число.
Формулы корней простейших тригонометрических уравнений

Уравнение переносом слагаемого и делением обеих частей легко сводится к простейшему. Разделим обе части на 4. О: t Примеры уравнений.

Ответ : Уравнение уже имеет простейший вид Это частный вид уравнения cos t=a a=0 Примеры уравнений.

tg (3x + π/4 ) +1 = 0. РЕШЕНИЕ: tg (3x + π/4 ) = -1; 3x + π/4 = -π/4 + πn, nЄZ; 3x = -π/4 - π/4 + πn, nЄZ; 3x = -π/2 + πn, nЄZ; x = -π/6 + π/3n, nЄZ; ОТВЕТ: x = -π/6 + π/3n, nЄZ.

Запомни Частные случаи решений уравнения |a|< 1 а=0 а=1 а=-1

Свойства аркфункций

Закрепление знаний и умений. Работа с учебниками (№81, №82, стр 59 Учебник. Алгебра и начала анализа. 10 класс. А. Е. Абылкасымова.

Самостоятельная работа обучающего характера

Тренировочный тест тригонометрия тест

Реши сам Группа 1 Группа 2 Решите уравнения: 1. 1. 2. 2. 3. 3. n/n ответ код n/n ответ код 1 Решений нет С 5 М 2 К 6 Р 3 А 7 П 4 у 8 О

Реши сам Уровень А Уровень Б УРА САМ МОЛОДЦЫ

Домашнее задание «Алгебра и начала анализа» А.Е. Абылкасымова. стр.60 №87, 88.

Фронтальным опросом вместе с учащимися подводятся итоги урока: - Что нового узнали на уроке? - Испытывали ли вы затруднения при выполнении самостоятельной работы? - Какие пробелы в знаниях выявились на уроке? - Какие проблемы у вас возникли по окончании урока?

Спасибо, урок окончен!!! Спасибо, урок окончен!!!



![Арксинусом числа а называют такое число из отрезка [- П/2; П/2], синус которого равен а. arcsin а П/2 - П/2 а arcsin (-a)=-arcsin a -а -arcsin а Арксинус и решение уравнений sin t=a. у х 0 1 -1 Арксинусом числа а называют такое число из отрезка [- П/2; П/2], синус которого равен а. arcsin а П/2 - П/2 а arcsin (-a)=-arcsin a -а -arcsin а Арксинус и решение уравнений sin t=a. у х 0 1 -1](https://fs3.ppt4web.ru/images/133572/193763/640/img0.jpg)
![П 0 arccos а Арккосинусом числа а называют такое число из промежутка [0;П ], косинус которого равен а а arccos (-a)=-П-arccos a -а П-arccos a Арккосинус и решение уравнений соs t=a. у х 0 1 -1 П 0 arccos а Арккосинусом числа а называют такое число из промежутка [0;П ], косинус которого равен а а arccos (-a)=-П-arccos a -а П-arccos a Арккосинус и решение уравнений соs t=a. у х 0 1 -1](https://fs3.ppt4web.ru/images/133572/193763/640/img1.jpg)