Презентация на тему: Решение простейших тригонометрических уравнений (2-й час)

Решение простейших тригонометрических уравнений (2-й час) Цель: продолжить формирование умений решать тригонометрические уравнения; систематизировать знания по теме; содействовать развитию математического мышления.

1. Повторение Вычислите: 1. arcsin

Что вы знаете о тригонометрических уравнениях? Запишите:Тригонометрические уравнения

Решить уравнения:

Решение уравнений вида: tg х=а и ctg х=аРешите:

Методы решения тригонометрических уравнений Это нужно помнить:Решение тригонометрических уравнений сводится к преобразованию тригонометрических выражений, входящих в уравнение, таким образом, чтобы рассматриваемое уравнение привелось к нескольким простейшим уравнениям, которые решаются стандартным способом.В каждом конкретном примере используется свой способ преобразования. Успех в решении тригонометрических уравнений будет достигнут при хорошем знании тригонометрических формул и умений грамотно проводить тригонометрические преобразования.

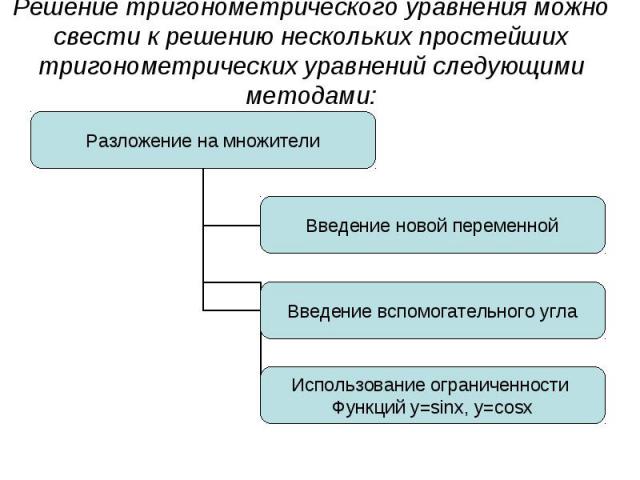
Решение тригонометрического уравнения можно свести к решению нескольких простейших тригонометрических уравнений следующими методами: разложение на множителивведение новой переменнойвведение вспомогательного углаиспользование ограниченности функций y=sin x, y=cos x

Решение тригонометрического уравнения можно свести к решению нескольких простейших тригонометрических уравнений следующими методами:

Метод разложения на множители При решении тригонометрического уравнения методом разложения на множители можно пользоваться всеми известными способами разложения на множители алгебраических выражений: вынесение за скобки общего множителя, группировка, применение формул сокращенного умножения. В некоторых случаях используются формулы:Сложения аргументов тригонометрических функцийПонижения степени тригонометрических функцийПреобразования произведения тригонометрических функций в суммуПреобразования суммы тригонометрических функций в произведение. Путем разложения на множители тригонометрическое уравнение приводится к виду, когда левая часть – произведение тригонометрических функций, а правая часть – нуль. Таким образом, исходное уравнение распадается на несколько простых уравнений.

Метод введения новой переменной исходное уравнение приводится к алгебраическому относительно тригонометрической функции одного аргумента, затем решается полученное алгебраическое уравнение, что приводит к нескольким простейшим тригонометрическим уравнениям. До введения новой переменной при необходимости нужно делать некоторые тождественные преобразования.

Метод введения новой переменной В некоторых случаях тригонометрические уравнения можно свести к алгебраическим относительно tgx. Примерами таких уравнений могут служить однородные уравнения.1. Уравнение вида: a sin kx + b cos kx =0 (a0, b0) называется однородным относительно sin kx, cos kx. Для того чтобы решить данное уравнение, разделим обе его части на cos kx. При этом потери корней не происходит, т.к. если cos kx=0, то из уравнения следует, что и sin kx=0, что невозможно, поскольку sin2 kx + cos2 kx =1. В результате получится уравнение a tg kx+b=0.Уравнение вида a sin2 kx + в sin kx cos kx + с cos2 kx=0 (a0). Разделив обе части уравнения на cos2 kx, получим равносильное уравнение: a tg2 kx + b tg kx + c= 0

Метод введения вспомогательного угла Суть метода введения вспомогательного угла заключается в том, что некоторую величину представляют как тригонометрическую функцию соответствующего аргумента, а затем проводят тригонометрические преобразования.

Формулы сложенияПродолжи формулу:

Запишите формулы: …тангенса суммы и разности…суммы и разности тангенсов…котангенса суммы и разности…суммы и разности котангенсов

Решите уравнение: Уровень А Уровень В, а) Sin x = 1 а) sin2x = 1 а) 1+ sin x = 0, б) 3 cos x – 2 sin 2 x = 0Уровень С а) Sin2 x = 0 б) 1+ 3 sin 2 x = 2 sin 2x, в) сos 4x – cos 2x= 0

Д/з: Повторить все о триг.урав; частные случаи, методы решения№