Презентация на тему: Особые приёмы решения логарифмических неравенств с переменной в основании Занятие №2

Особые приёмы решениялогарифмических неравенств с переменнойв основанииЗанятие №2Методическая разработкаучителя Поляковой Е. А.

Решение простейших логарифмических неравенств:

В предыдущем занятии было доказано:выраженияlog a b и (b – 1)(a – 1)имеют один знак

Решение логарифмических неравенств с применением доказанного свойства:неравенство log h(x) f(x) > log h(x) g(x) равносильно неравенству (f – g)(h – 1) > 0 на ОДЗ неравенство log h(x) f(x) < log h(x) g(x) равносильно неравенству (f – g)(h – 1) < 0 на ОДЗ

Алгоритм решения неравенства log h(x) f(x) > log h(x) g(x) 1) Находим область допустимых значений переменной (ОДЗ):(Условимся далее две последние строки системы писать одной так: 0 < h(x) ≠ 0)2) Решаем неравенство (f(х) – g(х))(h(х) – 1) > 0. 3) Для найденного решения учитываем ОДЗ.4) Записываем ответ.

Решите неравенство:2) Переписываем неравенство в видеРешаем неравенство (х – 1 – (х – 3) 2)(х – 3 – 1) < 0;

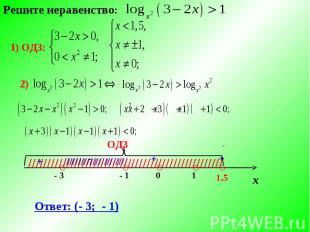
Решите неравенство:

Решите неравенство:

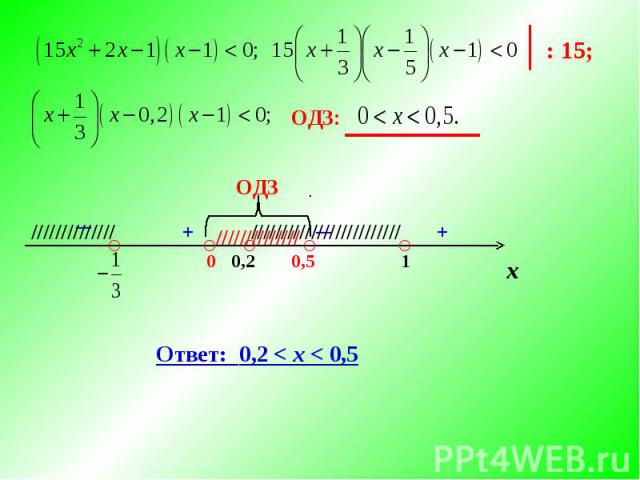
Решите неравенство:

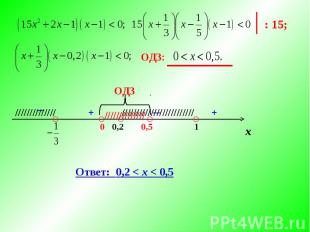
Ответ: 0,2 < x < 0,5

1) Решите неравенство:2) Решите неравенство:

Продолжение следует, до новых встреч