Презентация на тему: Особые приёмы решения логарифмических неравенств с переменной в основании Занятие №1

Особые приёмы решениялогарифмических неравенств с переменнойв основанииЗанятие №1Методическая разработкаучителя Поляковой Е. А.

Неравенство, содержащее переменную под знаком логарифма, называется логарифмическим. Например, неравенства вида:При а > 0, а ≠ 1 являются логарифмическим

Решение простейших логарифмических неравенств:

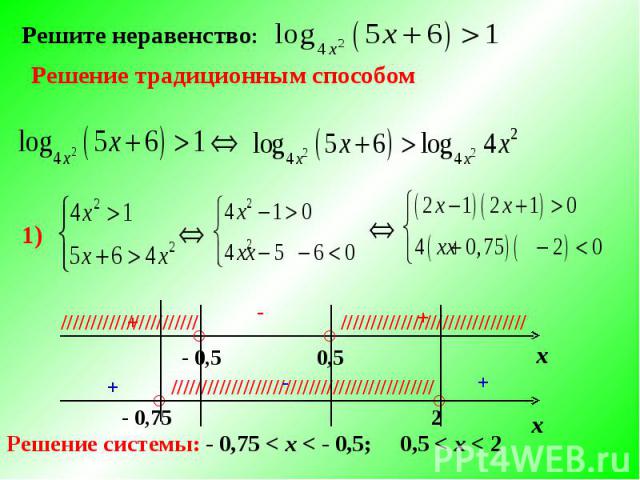
Решите неравенство:Решение традиционным способом

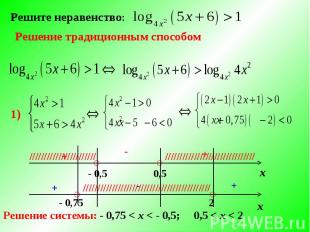
Решите неравенство:Решение традиционным способом

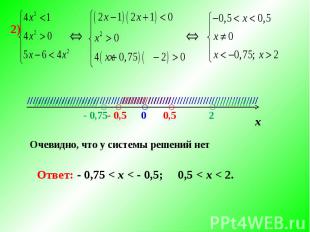
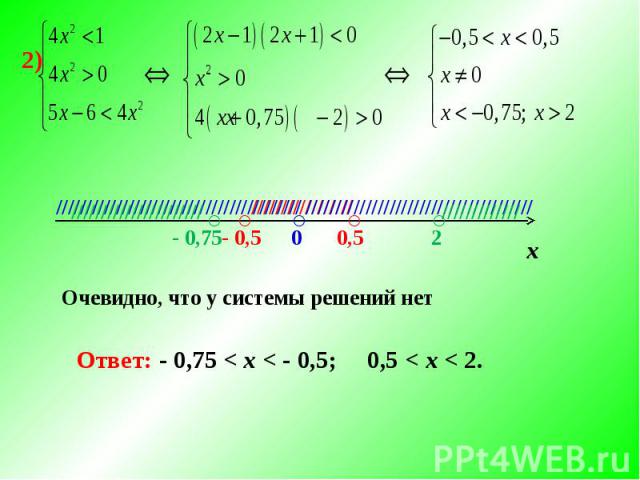
Очевидно, что у системы решений нет

Интересное заключениео знакахдвух выражений

Докажем, например, что log а b > 01) Перейдём к основанию, например, 22) Неравенство log а b > 0 перепишем в виде 3) Дробь положительна, если числитель изнаменатель одинаковых знаков, тогда

Доказано, что выражения log а b и (b – 1)(а – 1) одинаковых знаков.Это свойство используется при решении логарифмических неравенств, где выражение log а b можно заменить выражением (b – 1)(а – 1) того же знакаЧтобы не возникало проблем, необходимо находить ОДЗ переменной, так как формальная замена приводит к расширению области определения неравенства

Доказать, что при всех допустимых значениях переменной х 2) Неравенство log h f (х) > log h g(х) перепишем в виде 3) Дробь положительна, если числитель и знаменательодинаковых знаков, тогда

Логарифмическая функция с основанием 2 возрастающая, тогда Доказано - неравенство log h(x) f(x) > log h(x) g(x) равносильно неравенству (f – g)(h – 1) > 0 на ОДЗ

Решение логарифмических неравенств с применением доказанного свойстваНеравенство log h(x) f(x) > log h(x) g(x) равносильно неравенству (f – g)(h – 1) > 0 на ОДЗАналогично неравенство log h(x) f(x) < log h(x) g(x) равносильно неравенству (f – g)(h – 1) < 0 на ОДЗ

Алгоритм решения неравенства log h(x) f(x) > log h(x) g(x) 1) Находим область допустимых значений переменной (ОДЗ):(Условимся далее две последние строки системы писать одной так: 0 < h(x) ≠ 0)2) Решаем неравенство (f(х) – g(х))(h(х) – 1) > 0. 3) Для найденного решения учитываем ОДЗ.4) Записываем ответ.

Решите неравенство:2) Переписываем неравенство в видеРешаем неравенство (х – (2х – 3))(2х – 3 – 1) > 0;

Решите неравенство:

Решите рассмотренным способом неравенстваРешения – в материалах следующего занятия

Продолжение следует, до новых встреч