Презентация на тему: Функция y=ax2+bx+c, её свойства и график

Тема: Функция y=ax2+bx+c, её свойства и график Цель урока: - ввести алгоритм построения графика функции y=ax2+bx+c; - рассмотреть свойства данной функции; - формировать умение строить график данной функции. «Весь анализ бесконечных вращается вокруг переменных величин и их функций» Л.Эйлер

Самостоятельная работа На координатной плоскости с помощью шаблонов построить график данных функций. В. 1. В.2.1) y = 2 x2–1 1) y = 0,5 ( x + 2 )22) y =-2(x+3)2 -2 2) y = - (x - 3)2 + 63) y =1/2(x-3)2 3) y = 2 x 2 - 3

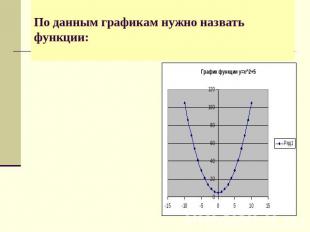
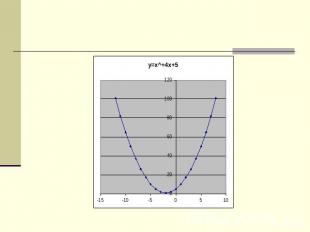
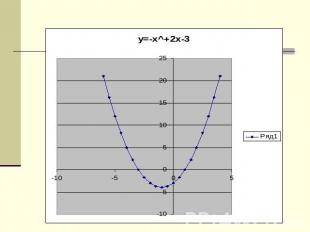
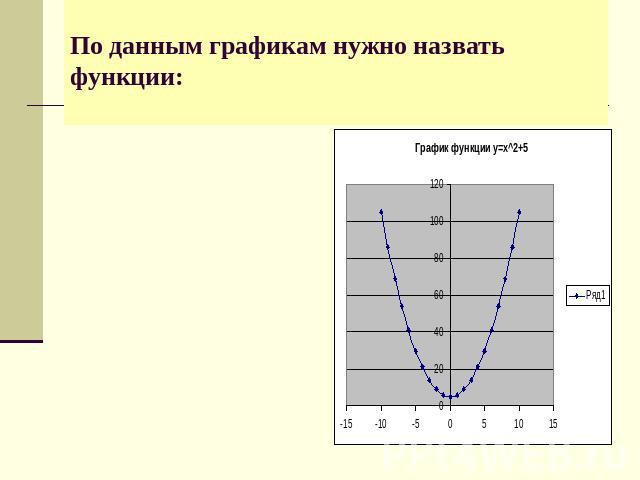
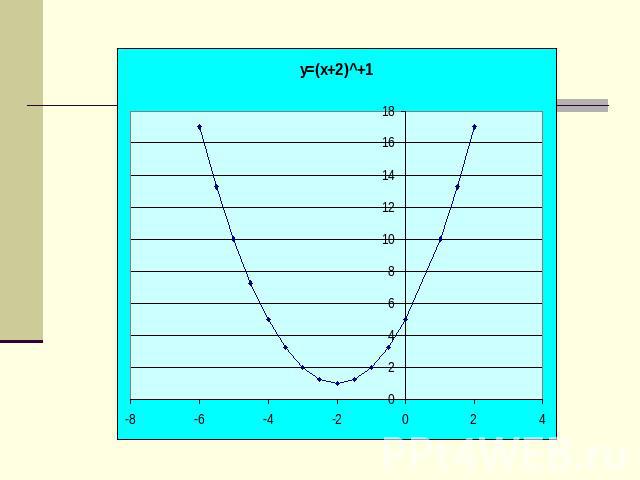
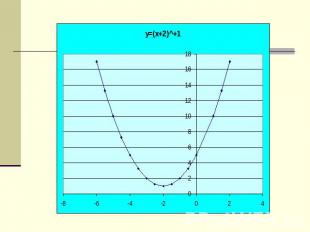
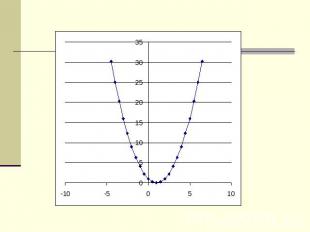
По данным графикам нужно назвать функции:

3. Заменить звёздочки числами таким образом, чтобы равенства стали верными. а) а 2 -2а * +в 2 = (а - *)2 б) 4u2 – 8u v + *2 =(2u-*)2 в) x2 +6x + *2 = (x + *)2 г) 9 – 2y * +*2 = (3 - *)24. Выделить полный квадрат из трёхчлена: а) x2 – 8x +14 = б) x2 + 6x + 10 =

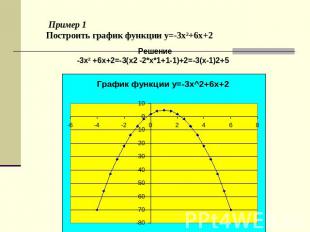
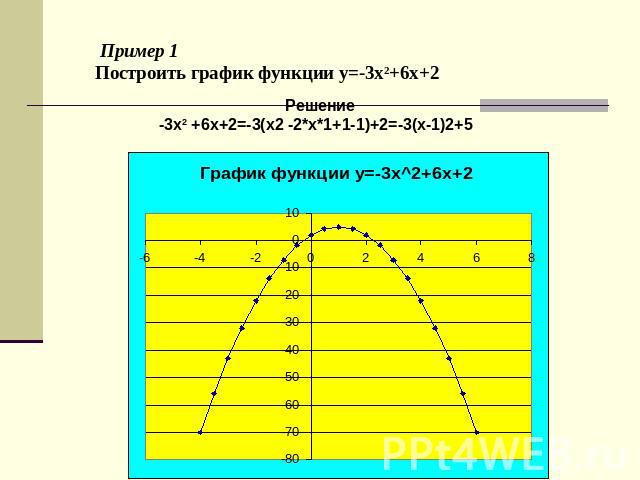
Пример 1Построить график функции y=-3x2+6x+2 Решение-3x2 +6x+2=-3(x2 -2*x*1+1-1)+2=-3(x-1)2+5

Вершиной параболы служит mочка (-L;m), осью параболы является прямая x = - L, т. е. x = -.b\2aВывод: Осью параболы y = ax2 + bx + c служит прямая x = - b\2a; абсцисса x0 вершины параболы y = ax2 + bx + c вычисляется по формуле x0 = -d\2a . Формулу для ординаты вершин параболы запоминать не нужно ( y0 = ) y0 = f(x0) !

Вывод! Не строя график можно ответить на вопросы:1) Куда направлены ветви параболы.2) Найти уравнение оси параболы.3) Найти координаты вершины параболы.Например: 1) у = 4 x 2 + 8x - 1; 2) y = - 3 x2 - 6x + 2; 3) y = - x 2 + x - 1; 4) y = 5 x 2 - 10x + 2.

Закрепление.1. Назовите коэффициенты a, b и c квадратичной функции:а) у = 7 x 2 – 3 x 2 - 2; в) у = 8 x 2 - 2x; б) у = 0,5 x 2 + 1; г) у=0,4x+1\7-3\10x2; 2. Запишите уравнение прямой, которая является осью симметрии параболы: а) у=2x2-x+1 ; в) у=7x2+12x+4;б) у=-5x2+2x-2 ; г) у=6x2+9x-3; 3. Найти координаты вершины параболы:а) у=-4x2+8x-1; б) у= -x2+x-1; в) у=-3x2-6x+2;

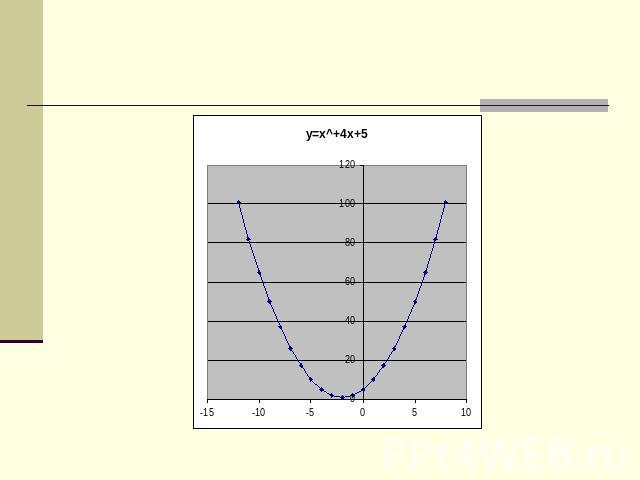
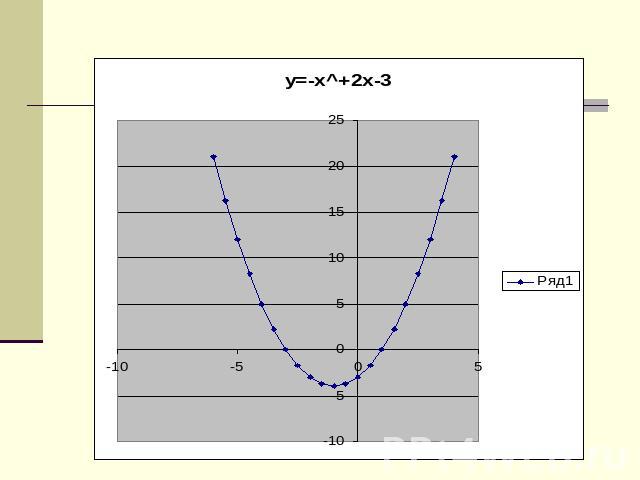
Построить графики функции: У = -х 2 + 2х - 32) У = x2 + 4х - 13) У = х2 - 4х

ИТОГ УРОКА