Презентация на тему: Графический способ решения квадратных уравнений

Графический способ решения квадратных уравнений

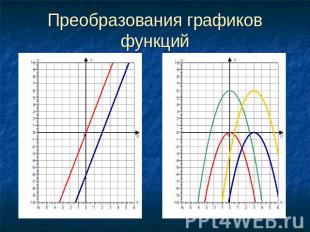
Преобразования графиков функций

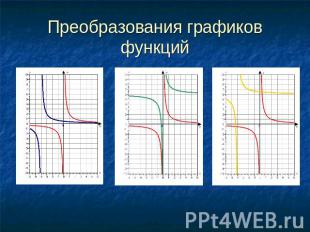
Преобразования графиков функций

Алгоритм построения параболынайти координаты вершины; провести ось параболы;отметить на оси абсцисс две точки, симметричные относительно оси параболы; найти значения функции в этих точках;провести параболу через полученные три точки.

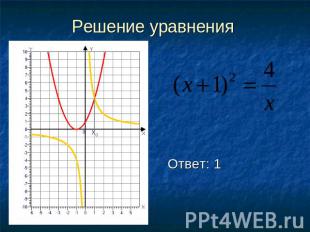
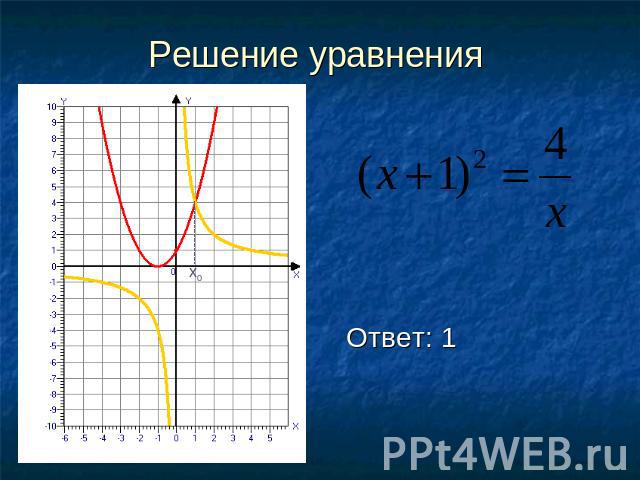
Решение уравнения

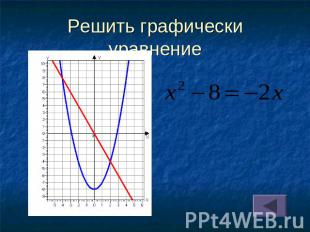
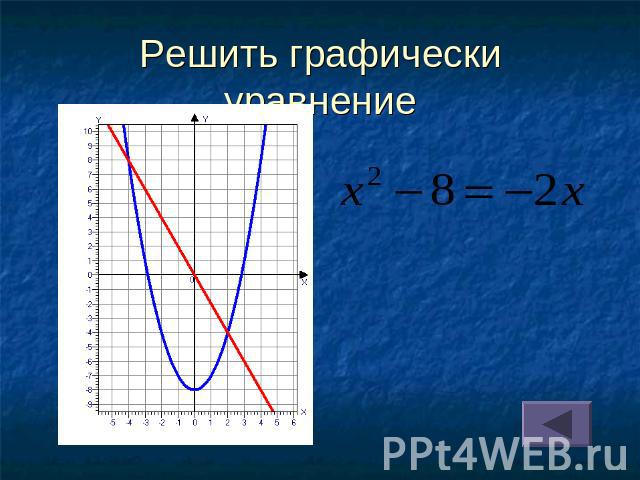
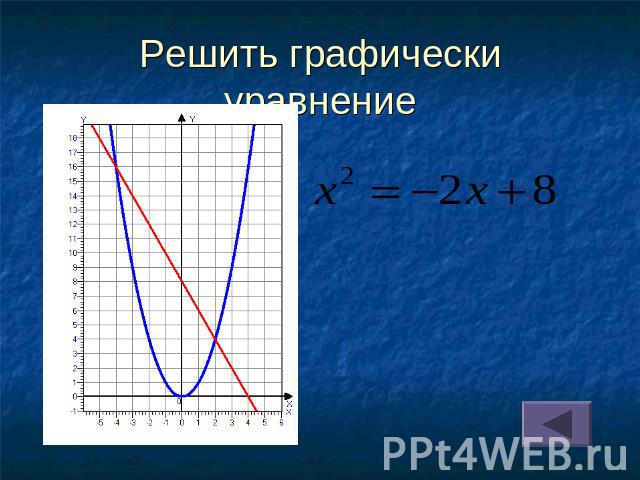
Решить графически уравнение

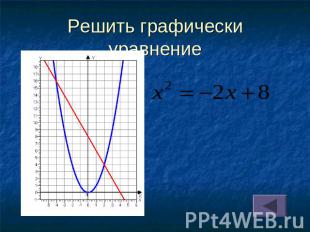
Решить графически уравнение

Решить графически уравнение

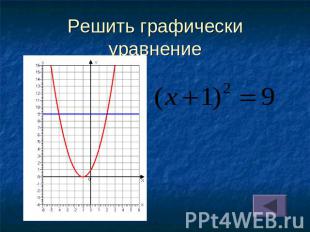
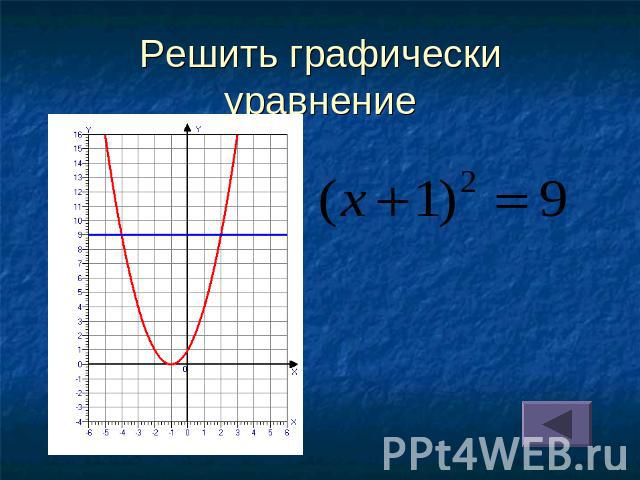
Решить графически уравнение

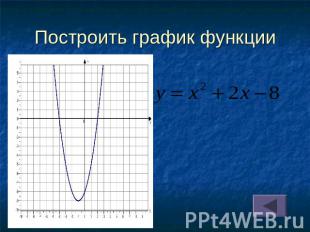
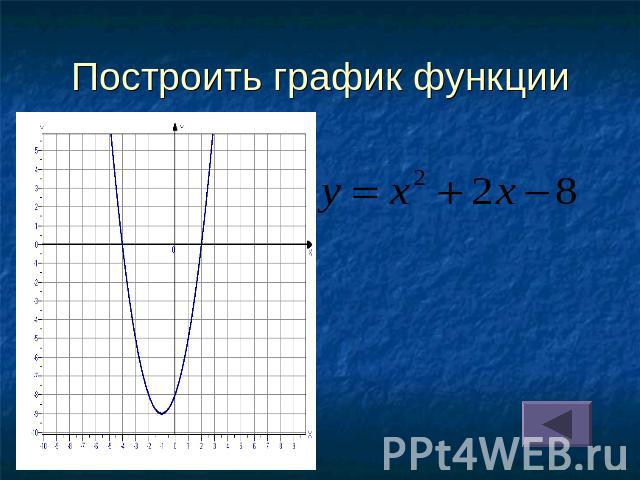
Построить график функции

Как решить уравнение?Построить график квадратичной функции и абсциссы точек пересечения параболы с осью x будут являться корнями уравнения.Выполнить преобразование уравнения, рассмотреть функции, построить графики этих функций, установить точки пересечения графиков функций, абсциссы которых и будут являться корнями уравнения.

Как можно преобразовать следующее уравнение?

Способы преобразования:

Алгоритм решения квадратного уравнения графическим способомСпособ 1Построить график функции y=ax2+bx+cНайти точки пересечения графика с осью абсцисс

Алгоритм решения квадратного уравнения графическим способомСпособ 2Преобразовать уравнение к виду ax2 = -bx-cПостроить:параболу y=ax2 и прямую y=-bx-cНайти точки их пересечения

Алгоритм решения квадратного уравнения графическим способомСпособ 3Преобразовать уравнение к виду ax2+с = -bxПостроить:параболу y = ax2+с и прямую y = -bxНайти их точки пересечения

Алгоритм решения квадратного уравнения графическим способомСпособ 4 (выделение полного квадрата)Преобразовать уравнение к виду a(x+l)2 = -mПостроить:параболу y = a(x+l)2 и прямую y = -mНайти точки их пересечения

Алгоритм решения квадратного уравнения графическим способомСпособ 5Преобразовать уравнение к виду

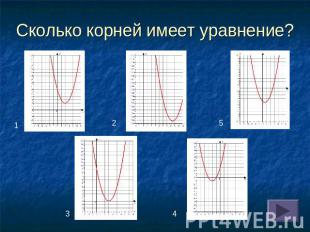
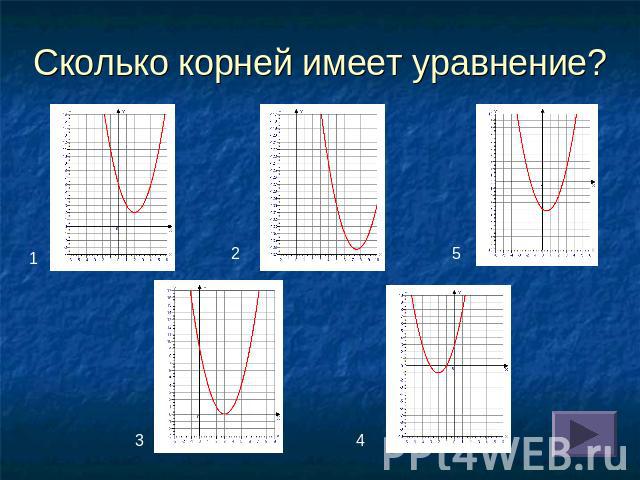
Сколько корней имеет уравнение?

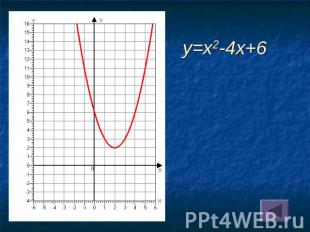
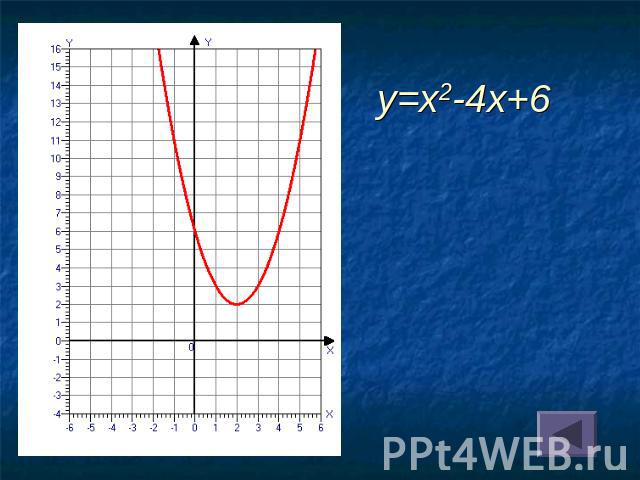
y=x2-4x+6

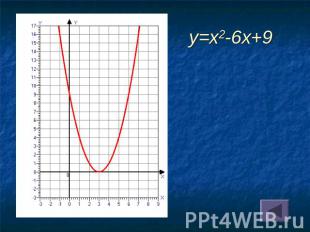
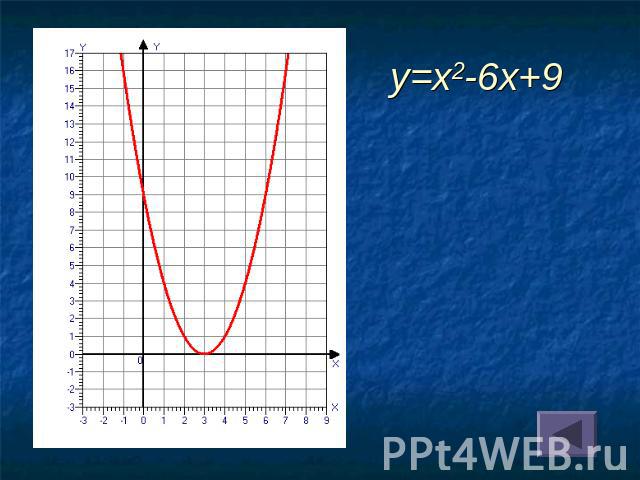
y=x2-6x+9

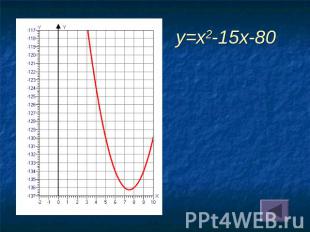
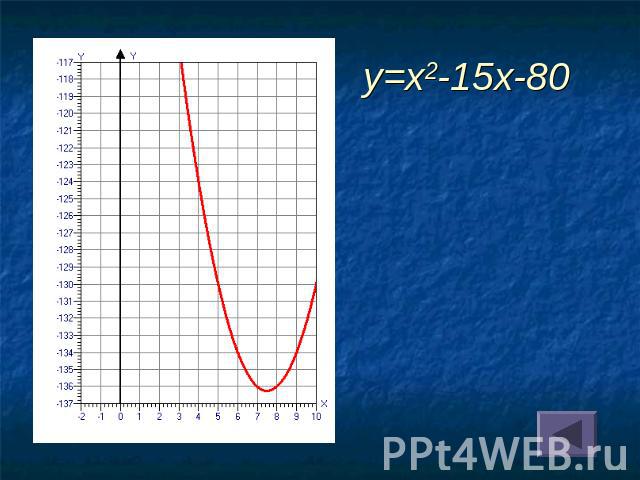
y=x2-15x-80

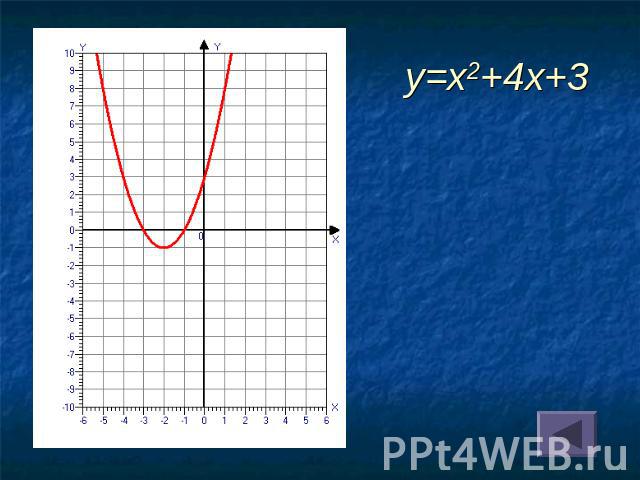
y=x2+4x+3

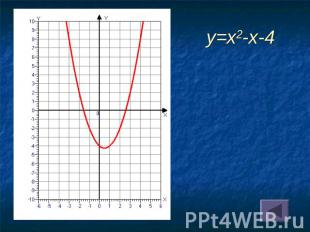
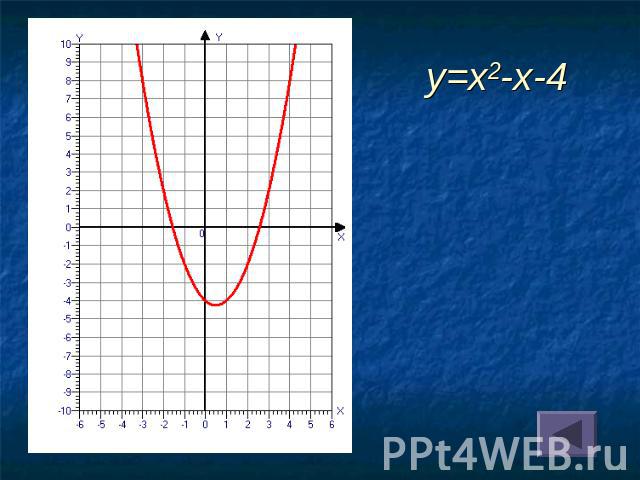
y=x2-x-4

Итог Познакомились: с графическим методом решения квадратных уравнений;с различными способами графического решения квадратных уравнений.закрепили знания по построению графиков различных функций.