Презентация на тему: Проверка качества уравнения регрессии

Проверка качества уравнения регрессии Коэффициент множественной корреляции: принимает значения в диапазоне 0 ≤ R ≤ 1. Чем ближе он к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Линейный коэффициент множественной корреляции (совокупный): Нелинейный квази-коэффициент детерминации:

Скорректированный (улучшенный) коэффициент множественной детерминации где n – число наблюдений, m – число параметров при переменных х. Чем больше величина m, тем больше различия между коэффициентом множественной детерминации и скорректированным коэффициентом. Чем больше объем совокупности, по которой исчислена регрессия, тем меньше различия между данными коэффициентами.

Оценка значимости уравнения множественной регрессии (F-критерий): Н0: уравнение статистически не значимо где m – число независимых переменных в уравнении регрессии; n – число единиц совокупности. Если Fфакт > Fтабл, то Н0 о случайной природе связи отклоняется и признается статистическая значимость и надежность уравнения. Если Fфакт < Fтабл, то Н0 не отклоняется и признается статистическая незначимость уравнения регрессии.

Частный F-критерий: оценивает статистическую значимость присутствия каждого из факторов в уравнении - коэффициент множественной детерминации для модели с полным набором факторов; - тот же показатель, но без включения в модель фактора х1; n – число наблюдений; m – число параметров при переменных х.

t-критерий Стьюдента: где mbi – средняя квадратическая ошибка коэффициента регрессии bi, она может быть определена по формуле: или

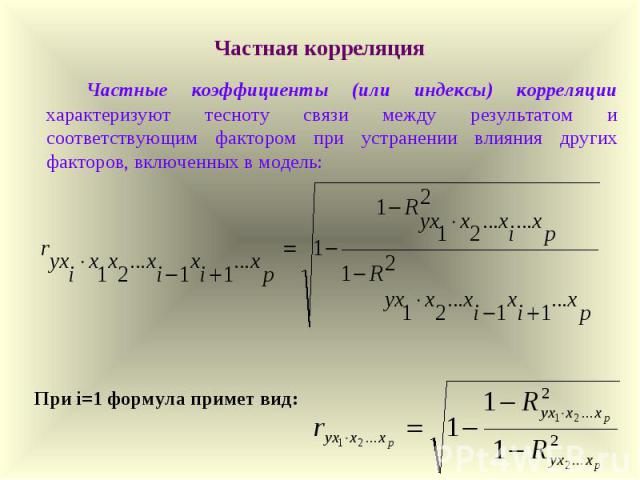
Частная корреляция Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в модель: При i=1 формула примет вид:

Частная корреляция первого порядка – когда фиксируется теснота связи двух переменных при устранении влияния одного фактора: (точка отделяет фактор, значение которого элиминируется (закрепляется на неизменном уровне)). Частная корреляция второго и т.д. порядка – когда фиксируется теснота связи двух переменных при устранении влияния двух и более факторов, например: - частная корреляция второго порядка при постоянном действии факторов х2 и х3; - частная корреляция четвертого порядка при постоянном действии факторов х2, х3, х4, х5.

Коэффициенты частной корреляции более высоких порядков можно найти через коэффициенты частной корреляции более низких порядков по рекуррентной формуле: При i=1 и двух факторах формула примет вид: При i=2 и двух факторах:

Предпосылки метода наименьших квадратов Требования, предъявляемые к ε: Несмещенность – означает, что математическое ожидание остатков равно нулю: т.е. при большом числе наблюдений остатки не будут накапливаться и найденный параметр регрессии b можно рассматривать как среднее значение из возможного большого количества несмещенных оценок. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным выборкам. 2.Эффективность – оценки считаются эффективными, если они характеризуются наименьшей дисперсией. 3.Состоятельность – характеризует увеличение точности оценок с увеличением объема выборки.

Предпосылки метода наименьших квадратов: случайный характер остатков; нулевая средняя величина остатков, не зависящая от х; гомоскедастичность; отсутствие автокорреляции остатков; нормальное распределение остатков.

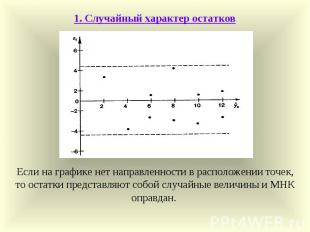
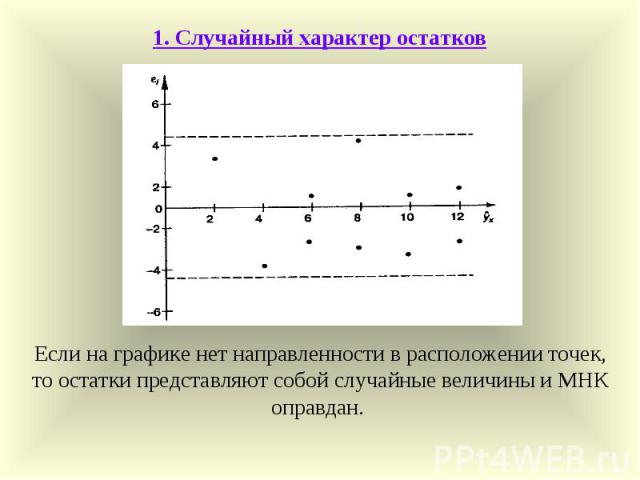
1. Случайный характер остатков Если на графике нет направленности в расположении точек, то остатки представляют собой случайные величины и МНК оправдан.

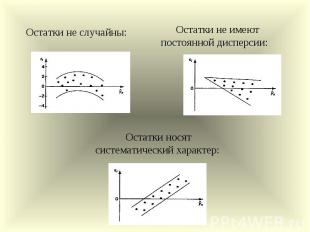
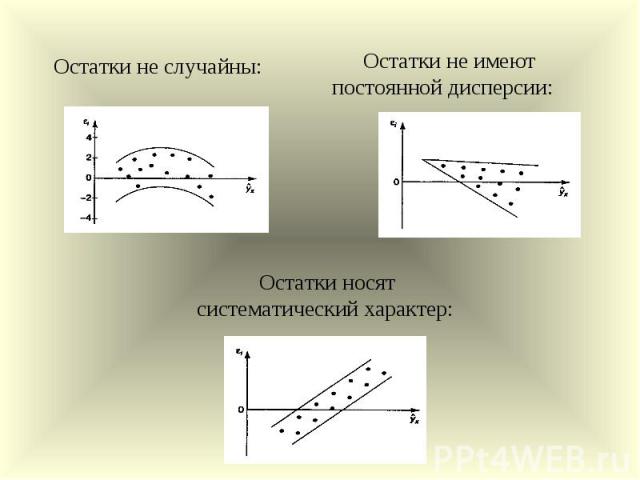
Остатки не случайны: Остатки не имеют постоянной дисперсии: Остатки носят систематический характер:

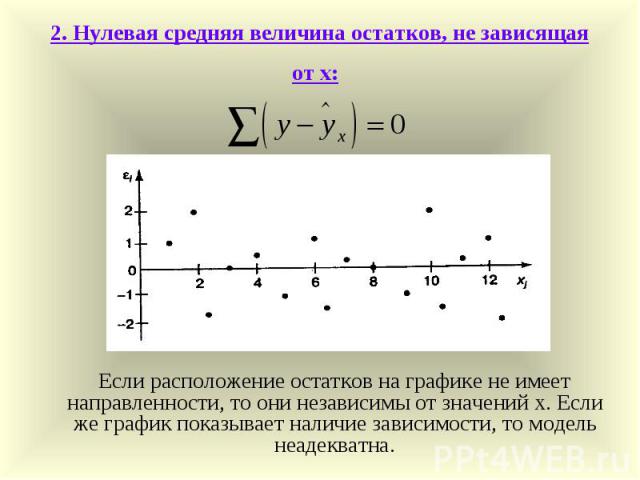
2. Нулевая средняя величина остатков, не зависящая от х: Если расположение остатков на графике не имеет направленности, то они независимы от значений х. Если же график показывает наличие зависимости, то модель неадекватна.

3. Гомоскедастичность Гомоскедастичность – это однородность относительно дисперсии, т.е. дисперсия остатков одинакова для каждого значения х. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность (неоднородность относительно дисперсии). Дисперсия остатков растёет по мере увеличения х: Дисперсия остатков достигает максимальной величины при средних значениях х Максимальная дисперсия остатков при малых значениях х

Методы проверки предпосылки МНК о гомоскедастичности остатков: Тест Гольдфельда-Квандта Тест ранговой корреляции Спирмена Тест Глейзера и другие.

4. Отсутствие автокорреляции остатков Под автокорреляцией остатков понимают зависимость распределения значений остатков друг от друга. Это означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Если этот коэффициент окажется существенно отличным от нуля, то остатки автокоррелированны.

Обобщенный метод наименьших квадратов (ОМНК)