Презентация на тему: Вычисление углов между прямыми и плоскостями

Вычисление угловмежду прямыми и плоскостями. 11 класс.

Цели урока: Показать, как используется скалярное произведение векторов при решении задач на вычисление углов между двумя прямыми, между прямой и плоскостью.

Повторяем теорию: Как находят координаты вектора, если известны координаты его начала и конца?Как находят координаты середины отрезка?Как находят длину вектора?Как находят расстояние между точками?Как вы понимаете выражение «угол между векторами»?

Повторяем теорию: Какие векторы называются перпендикулярными?Что называется скалярным произведением векторов?Чему равно скалярное произведение перпендикулярных векторов?Чему равен скалярный квадрат вектора?Скалярный квадрат вектора равен квадрату его длины.Свойства скалярного произведения?

Направляющий вектор прямой. Ненулевой вектор называется направляющим вектором прямой, если он лежит на самой прямой, либо на прямой, параллельной ей.
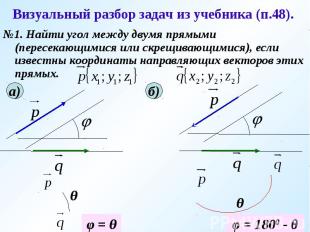
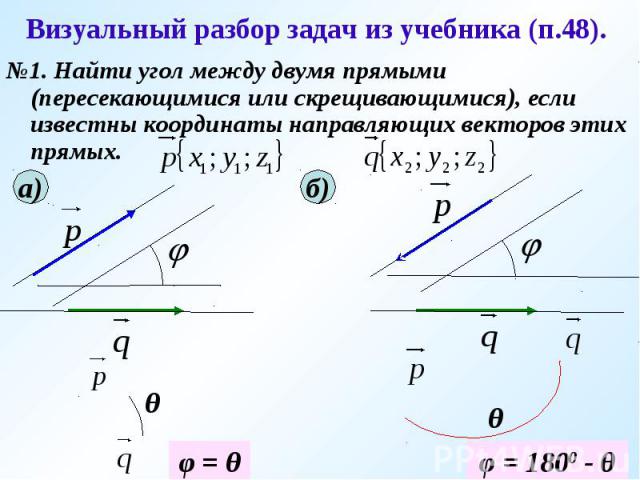
Визуальный разбор задач из учебника (п.48). №1. Найти угол между двумя прямыми (пересекающимися или скрещивающимися), если известны координаты направляющих векторов этих прямых.

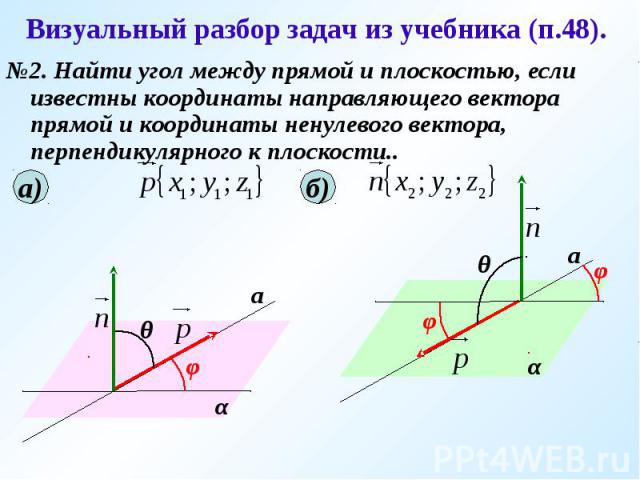
Визуальный разбор задач из учебника (п.48). №2. Найти угол между прямой и плоскостью, если известны координаты направляющего вектора прямой и координаты ненулевого вектора, перпендикулярного к плоскости..

№ 464 (а) Найти: угол между прямыми АВ и CD.Ваши предложения…Найдем координаты векторови2. Воспользуемся формулой:

Дано: куб АВСDA1B1C1D1 точка М принадлежит АА1 АМ : МА1 = 3 : 1; N – середина ВСВычислить косинус угла между прям. MN и DD11. Введем систему координат.2. Рассмотрим DD1 и МN.3. Пусть АА1= 4, тогда4. Найдем координаты векторов DD1 и MN.5. По формуле найдем cosφ.

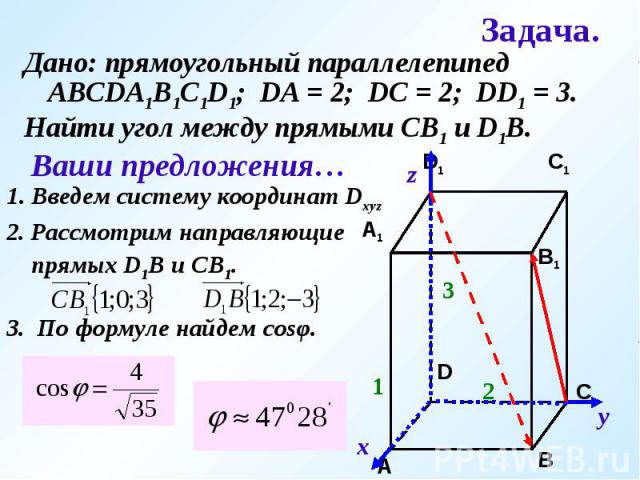
Дано: прямоугольный параллелепипед АВСDA1B1C1D1; DA = 2; DC = 2; DD1 = 3.Найти угол между прямыми СВ1 и D1B.Ваши предложения…1. Введем систему координат Dxyz2. Рассмотрим направляющие прямых D1B и CB1.3. По формуле найдем cosφ.
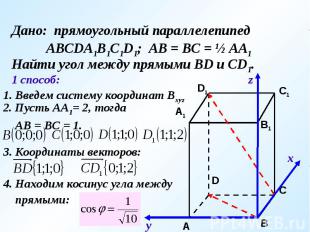
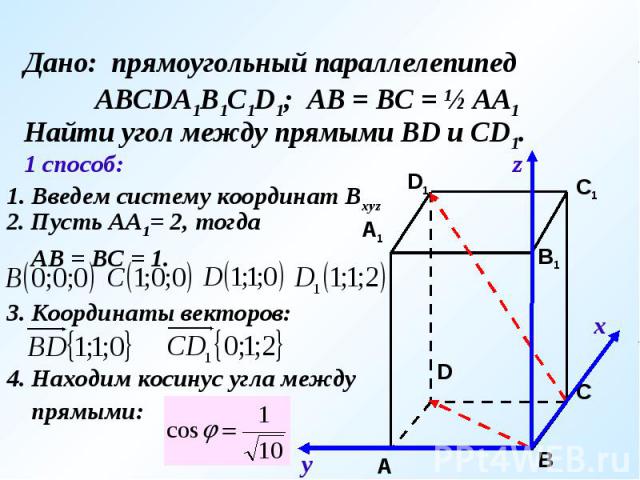
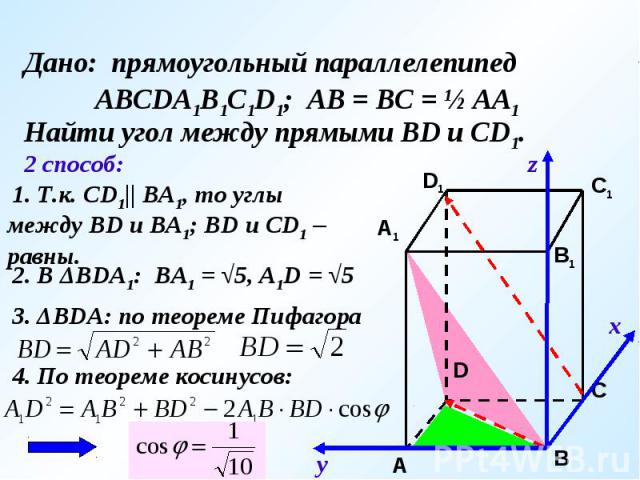
Дано: прямоугольный параллелепипед АВСDA1B1C1D1; АВ = ВС = ½ АА1Найти угол между прямыми ВD и CD1.1. Введем систему координат Bxyz2. Пусть АА1= 2, тогда АВ = ВС = 1.3. Координаты векторов:4. Находим косинус угла между прямыми:
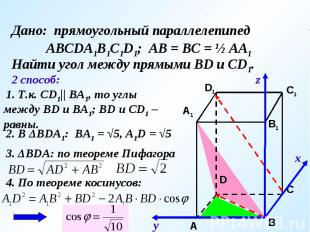
Дано: прямоугольный параллелепипед АВСDA1B1C1D1; АВ = ВС = ½ АА1Найти угол между прямыми ВD и CD1. 1. Т.к. СD1|| ВА1, то углы между ВD и ВА1; ВD и СD1 – равны. 2. В ΔВDА1: ВА1 = √5, А1D = √5 3. ΔВDА: по теореме Пифагора 4. По теореме косинусов: