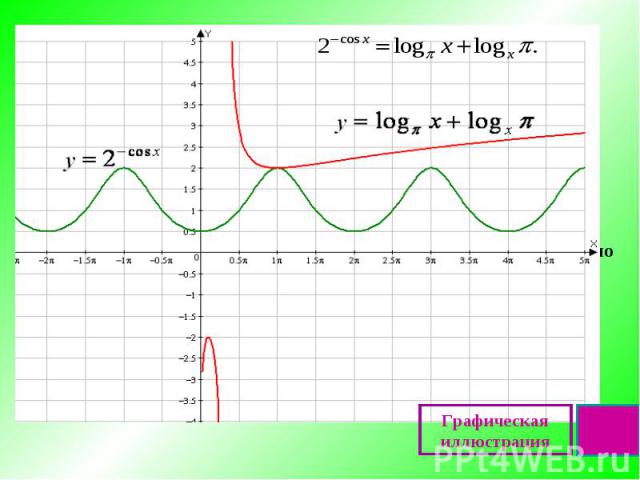
Презентация на тему: Применение свойств функций к решению уравнений и неравенств

Применение свойств функций к решению уравнений и неравенств Знакомство с методом мажорант

Метод мажорант На самом деле, вы встречались с этим методом, просто не знали, как он называется.Некоторые математики называют этот метод по-другому:«метод математической оценки»,«метод mini-max».Это очень красивый метод, и ему непременно следует научиться

Определение Мажорантой (от magiorante – главенствующий) данной функции f (х) на множестве D( f ) называется такое число М, чтолибо f(х) ≤ М для всех х ϵ D( f ),либо f(х) ≥ М для всех х ϵ D( f ).Метод мажорант или метод оценкииспользуется (чаще всего) в уравнениях вида f(x) = g(x) , где f(x) и g(x) – ограниченные функции,и на области определения данного уравнения наибольшее значение М одной из нихравно наименьшему значению М другой.

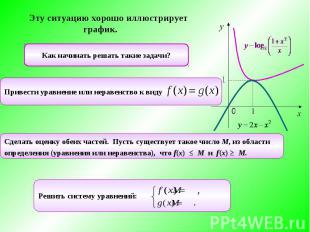
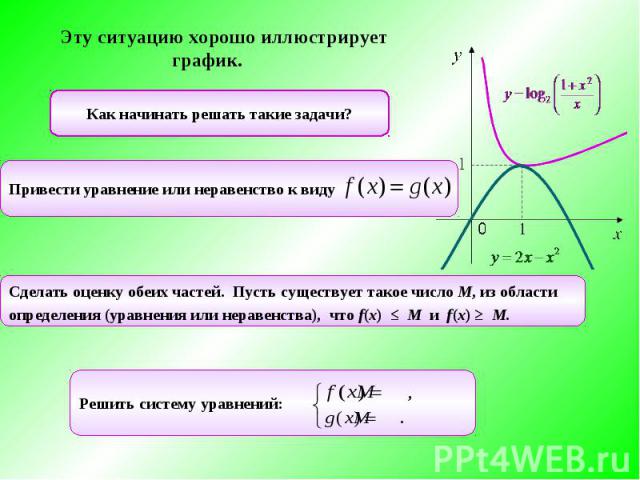
Эту ситуацию хорошо иллюстрирует график.       Как начинать решать такие задачи?Привести уравнение или неравенство к виду Сделать оценку обеих частей. Пусть существует такое число М, из областиопределения (уравнения или неравенства), что f(x) ≤ M и f(x) ≥ M.Решить систему уравнений:

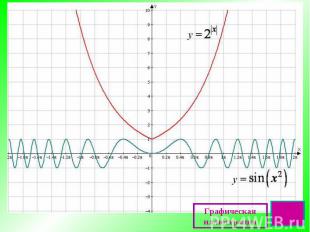
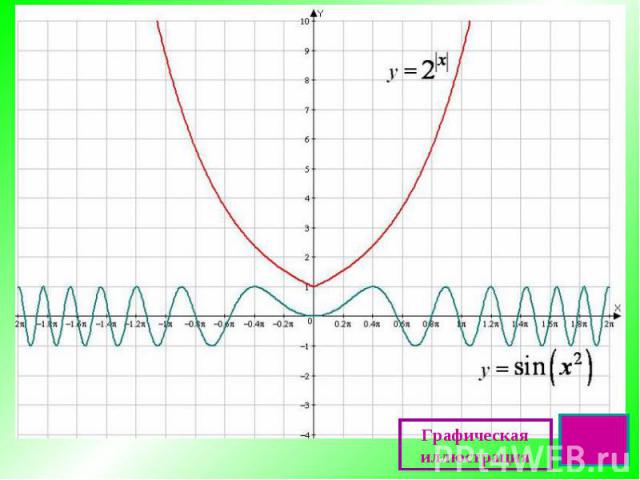
Графическая иллюстрация

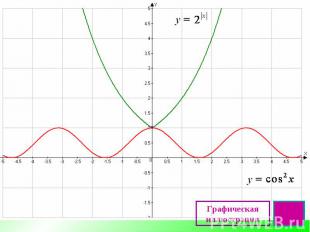
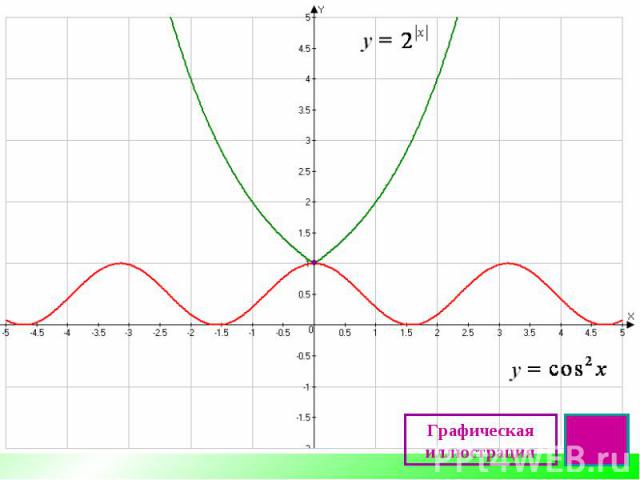
Графическая иллюстрация

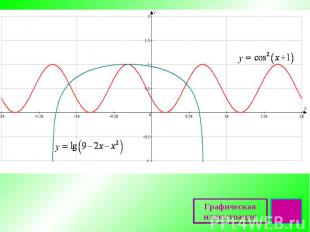
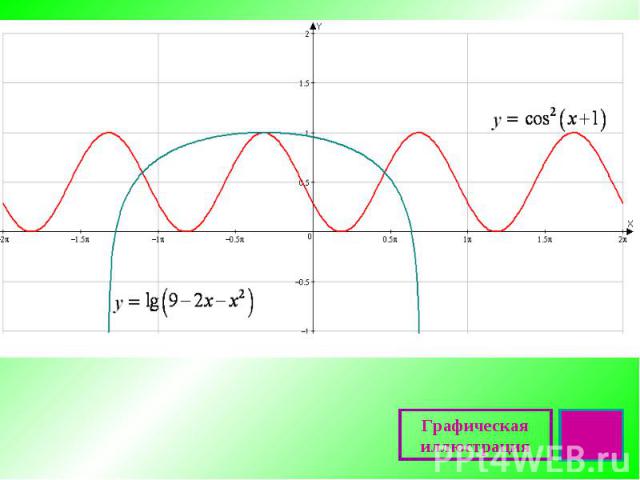
Графическая иллюстрация

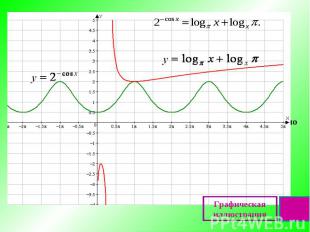
Графическая иллюстрация

Пример 5. Решить уравнение Решение. Оценим обе части уравнения. Поскольку - 1 ≤ sinx ≤ 1 и - 1 ≤ sin 9x ≤ 1, то выполняется тогда и только тогда, когда Решением первого уравнения системы являются значения

Пример 6. Решить уравнение Решение. Очевидно, что Заметим, что перемноживпочленно эти неравенства, получаем:Следовательно, левая часть равна правой, лишь при условии: Значит, данное уравнение равносильно системе уравнений: Решаясистемууравнений, получаем:

Пример 7. Решите уравнение Решение. Для решения уравнения оценим его части: Равенство возможно только при условииСначала решим второе уравнение: Проверим справедливость первого равенства, подставив эти корни:Итак, данное уравнение имеет единственный корень х = 0.

Пример 8. Найти все значения параметра а, при каждом из которых уравнение имеет решения. Найдите эти решения.Решение. Перепишем уравнение в виде При всех значениях х выражение При всех значения х выражения Следовательно, левая часть уравнения не меньше 4, а правая часть – не больше 4. Получаем систему: