Презентация на тему: Применение свойств функций к решению уравнений и неравенств

МОУ «Инсарская средняя общеобразовательная школа №1» ПОДГОТОВКА К ЕГЭПРИМЕНЕНИЕ СВОЙСТВ ФУНКЦИЙ К РЕШЕНИЮ УРАВНЕНИЙ И НЕРАВЕНСТВЧудаева Елена Владимировна, учитель математики, г. Инсар, Республика Мордовия

Содержание Метод мажорант (метод оценки)Использование свойств функций: Область определения Множество значений Четность и нечетность3. Задачи с параметром4. Задачи из сборника ЕГЭ, часть «С»5. Использованные источники

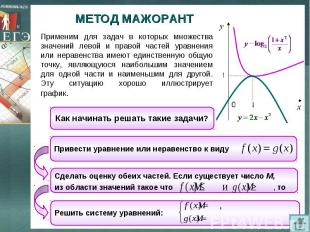
МЕТОД МАЖОРАНТ Применим для задач в которых множества значений левой и правой частей уравнения или неравенства имеют единственную общую точку, являющуюся наибольшим значением для одной части и наименьшим для другой. Эту ситуацию хорошо иллюстрирует график.       

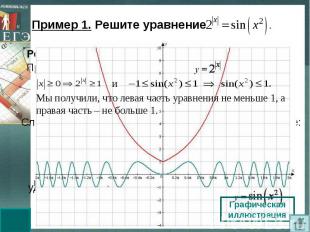
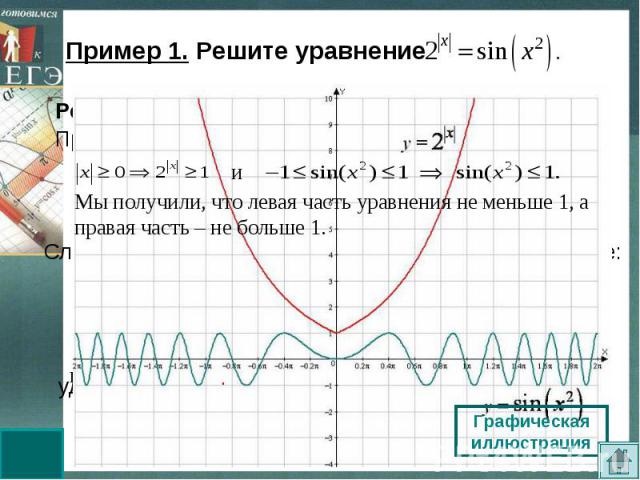
Пример 1. Решите уравнение Мы получили, что левая часть уравнения не меньше 1, а правая часть – не больше 1.

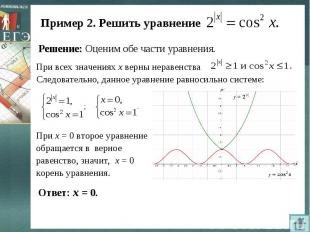
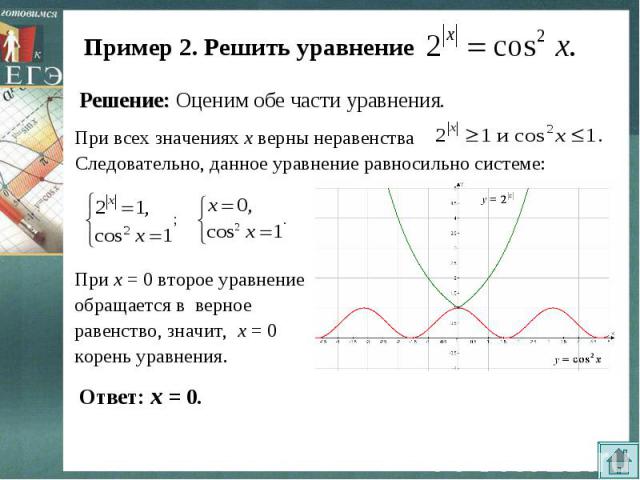
Пример 2. Решить уравнение Решение: Оценим обе части уравнения.При всех значениях х верны неравенстваСледовательно, данное уравнение равносильно системе:При х = 0 второе уравнение обращается в верное равенство, значит, х = 0 корень уравнения.

Пример 3. Решить неравенство Следовательно, исходное неравенство выполняется тогда и только тогда, когда оба множителя равны 1 одновременно. Получаем х = -1 – единственное решение системы уравнений, а, значит, и данного неравенства.

Пример 4. Решить уравнение Для правой части (в силу неравенства для суммы двух взаимнообратных чисел) выполнено Поэтому уравнение имеет решения, если и только если одновременно выполнены два условия Решая последнюю систему, получаем

Пример 5. Решить уравнение Решение. Оценим обе части уравнения. 1) Каждое слагаемое левой части уравнения не больше 1, следовательно их сумма будет равна 2, если они принимают своё наибольшее значение. Значит, уравнение равносильно системе: 2) Решая первое уравнение системы, находим : 3) Подставим найденные значения во второе уравнение:

Пример 6. Решить уравнение Решение. Оценим множители левой части уравнения.

Пример 7. Решите уравнение Решение. Для решения уравнения Поэтому равенство возможнотолько при условии:Проверим справедливость первого равенства, подставив эти корни. При

Пример 8. Найти все значения параметра а, при каждом из которых уравнение Решение. Перепишем уравнение в виде При всех значениях х выражение: Следовательно, левая часть уравнения не меньше 4, а правая часть – не больше 4. Получаем систему:

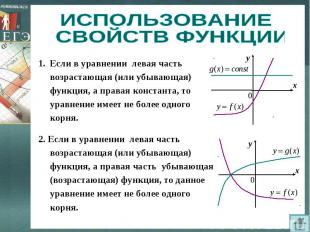
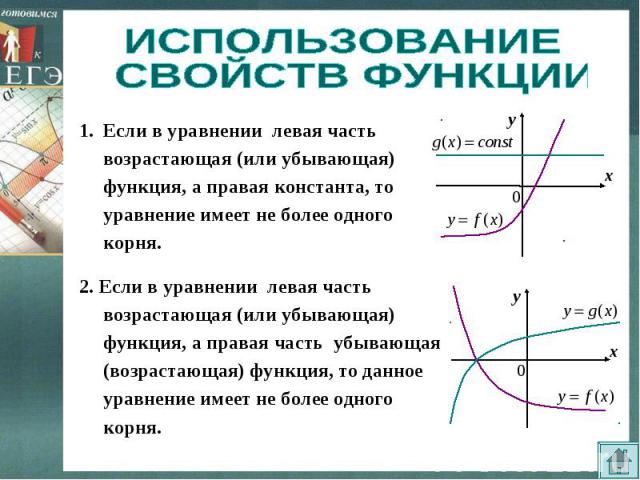
ИСПОЛЬЗОВАНИЕ СВОЙСТВ ФУНКЦИИ Если в уравнении левая часть возрастающая (или убывающая) функция, а правая константа, то уравнение имеет не более одного корня.2. Если в уравнении левая часть возрастающая (или убывающая) функция, а правая часть убывающая (возрастающая) функция, то данное уравнение имеет не более одного корня.

Пример 9. Решить уравнение Решение: Заметим, что х = 1 , является корнем данного уравнения. Левая часть уравнения представляет собой сумму двух возрастающих функций и, следовательно, сама является возрастающей функцией, принимающей каждое своё значение ровно один раз. Поэтому других корней данное уравнение не имеет.Ответ: 1.

Пример 10. Доказать, что уравнение не имеет решений:Арифметический корень не может быть отрицательным числом, поэтому уравнение решений не имеет.Левая часть исходного уравнения определена при , при каждом таком значении х Следовательно, их сумма всегда больше нуля. Не существует такого значения х, при котором оба выражения имеют смысл. Поэтому уравнение решений не имеет.

ИСПОЛЬЗОВАНИЕ ОБЛАСТИ ОПРЕДЕЛЕНИЯ ФУНКЦИИ Решить уравнение:Итак, единственной точкой, в которой определены эти радикалы, является x = 1. Легко проверить, что это число – корень уравнения.

Решить уравнение 1) Выпишем, условие существования функции, стоящей в левой части: 2) Проверим не отрицательность правой части: Последнее неравенство решений не имеет.3) Значит, исходное уравнение тоже не имеет решений, так как левая часть его – неотрицательная функция!

ИСПОЛЬЗОВАНИЕ СВОЙСТВА ОГРАНИЧЕННОСТИ ФУНКЦИИ ДЛЯ НАХОЖДЕНИЯ ЕЁ НАИБОЛЬШЕГО ЗНАЧЕНИЯУкажите наибольшее целое значение функцииДанная функция принимает наибольшее значение тогда и только тогда, когда наибольшее значение принимает функция, стоящая в показателе степени: Преобразуем её: равно 4. Следовательно, наибольшее значение исходной функции

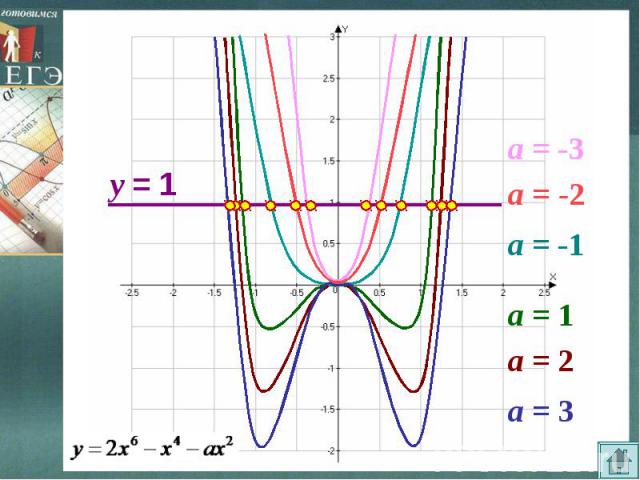
ИСПОЛЬЗОВАНИЕ ЧЕТНОСТИ ФУНКЦИИПример. Может ли при каком-нибудь значении параметра а, уравнение иметь три корня? Решение. Легко заметить, что при замене х на –х данное уравнение не изменится, значит, если от нуля, входят в множество решения уравнения «парами». Так как число 0 не является корнем уравнения, то уравнение имеет четное число корней.

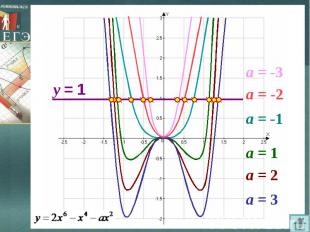
ИСПОЛЬЗОВАНИЕ ЧЕТНОСТИ ФУНКЦИИМожет ли при каком-нибудь значении параметра а, уравнение Так как при замене х на –х данное уравнение не изменится, то множество его корней вместе с каждым корнем содержит противоположный корень. Следовательно, уравнение имеет четное число корней, отличных от нуля. Проверка показывает, что 0 – корень, значит, данное уравнение имеет нечетное число корней.

Литература Математика. ЕГЭ. Контрольные измерительные материалы. Методические указания при подготовке. Тестовые задания: Учебно – методическое пособие Л.Д. Лаппо, А.В. Морозов, М.А. Попов. – М.: издательство «Экзамен», 2004, 2006, 20082. Математика. ЕГЭ. Контрольные измерительные материалы. Варианты тестов. Министерство образования РФ. – М.: Центр тестирования Минобразования России, 2002. Денищева Л.О. и др.3. Математика — абитуриенту. Автор: Ткачук В. В. Издательство: 2007. Год: МЦНМО. Страниц: 976Для создания шаблона презентации использовалась картинка http://www.box-m.info/uploads/posts/2009-05/1242475156_2.jpg