Презентация на тему: Решение систем линейных алгебраических уравнений с помощью определителей

Научно – практическая конференция школьников «Эврика»Решение системлинейных алгебраическихуравненийс помощью определителейНаучно – исследовательский проектВыполнен ученицей 10 «Б» классаСОШ № 74 г. КраснодараБаевой Татьяной ИвановнойНаучный руководитель – учитель математики СОШ № 74Забашта Елена Георгиевна

Цель:изучить свойства определителей и применить их в решении систем линейных алгебраических уравнений. Задачи исследования: рассмотрение схем вычисления определителей и их свойств; решение систем линейных алгебраических уравнений и некоторых задач аналитической геометрии с помощью определителей.

Определители второго порядка

Определители третьего порядка

Минор и алгебраическое дополнениеМинором какого либо элемента называется определитель, получаемый из данного определителя вычеркиванием той строки и того столбца, на пересечении которых стоит данный элемент.Алгебраическим дополнением элемента называется его минор, взятый со своим или противоположным знаком. согласно следующему правилу: если сумма номеров столбца и строки, на пересечении которых стоит элемент, есть число четное, то минор берется со своим знаком, если нечетное – то с противоположным.

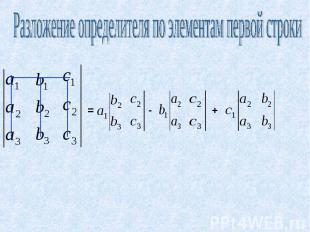
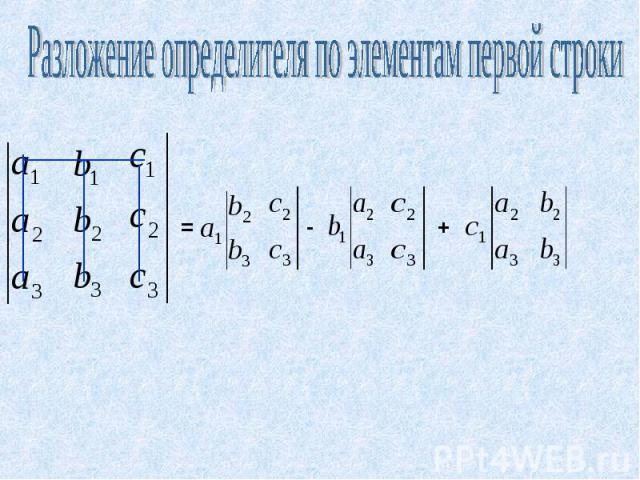
Разложение определителя по элементам первой строки

Свойства определителей Величина определителя не изменится при замене всех его строк соответствующими столбцами. При перестановке двух столбцов (или строк) определитель меняет знак. Определитель с двумя одинаковыми столбцами (или строками) равен нулю. Множитель, общий для элементов некоторого столбца (или строки) можно выносить за знак определителя. Определитель равен нулю, если все элементы некоторого столбца (или строки) равны нулю. Величина определителя не изменится, если к элементам некоторого столбца (строки) прибавить элементы другого столбца (строки), предварительно умножив их на один и тот же множитель.

Система двух линейных алгебраических уравненийс двумя неизвестными имеет единственное решение х = при условии, что определитель системы отличен от нуля, т.е.

Система трех линейных уравнений с тремя неизвестнымиимеет единственное решение х = , при условии, что определительсистемы не равен нулю

Однородная система двух уравнений с тремя неизвестными где k – произвольный множитель, если хотя бы один из определителей отличен от нуля. В случае, когда все определители равны нулю, система сводится к одному уравнению.Однородная система трех уравнений с тремя неизвестными имеет решение, отличное от нулевого, когда определитель системы равен нулю.

Некоторые приложения определителей к аналитической геометрии1. Площадь треугольника с вершинами вычисляется по формуле , где знак выбирается одинаковым со знаком определителя.2. Условие, при котором три точки 3. Уравнение прямой, проходящей через две данные точки 4. Условие, при котором три прямые пересекаются в одной точке:

Вычислить определитель Решение.1–ый способ. 2-ой способ.Прибавляя удвоенный второй столбец к первому, затем к третьему столбцу и применяя формулу, получим3-ий способ.

Вычислить площадь треугольника с вершинами А(1,-1), В(2,3), С(4,5).Решение.Вычислим соответствующий определитель:

Решить систему уравнений Решение.В данном случае: Определитель системы , поэтому х =

Спасибо за внимание