Презентация на тему: Решение систем линейных уравнений

Автор: Кокорина Людмила Николаевна, учитель математики Сюмсинской средней школы, Удмуртия 900igr.net

1.Что называют системой двух линейных уравнений с двумя переменными? 2.Знак системы? 3.Что называют решением системы двух уравнений с двумя переменными? 4.Что значит решить систему уравнений?

Способы решения систем двух линейных уравнений с двумя переменными 1.Способ подстановки 2.Способ алгебраического сложения 3.Графический способ 4.Формулы Крамера 5.Метод подбора

Способ подстановки 1.Из одного уравнения системы (всё равно из какого)выразить одну переменную через другую, например, y через x. 2.Полученное выражение подставить в другое уравнение системы и получить уравнение с одной переменной x. 3.Решить это уравнение, найти значение x. 4.Подставить найденное значение x в выражение для y и найти значение y. 5.Записать ответ в виде упорядоченной пары (x;y)

Решить систему уравнений методом подстановки -3x=-3 X=-3: (-3) X=1 y=4-2*1 y=2 Ответ: (1;2) 2x+y=4 y=4-2x X+2*(4-2x)=5 X+8-4x=5 X-4x=5-8

Способ алгебраического сложения 1.Уравнять модули коэффициентов при одной из переменных; 2.Складывая или вычитая полученные уравнения, найти значение одной переменной; 3.Подставить найденное значение в одно из уравнений исходной системы и найти значение второй переменной; 4. Записать ответ в виде упорядоченной пары (x;y).

Решить систему уравнений способом алгебраического сложения 3y=6 y=2 X+2y=5 X+2*2=5 X+4=5 X=1 Ответ: (1;2)

Графический способ 1.Выразить y через x из каждого уравнения системы 2.Построить графики функций в одной координатной плоскости. 3.Найти координаты общей точки графиков ( если графики имеют общую точку) 4 Записать ответ в виде x≈… И y≈

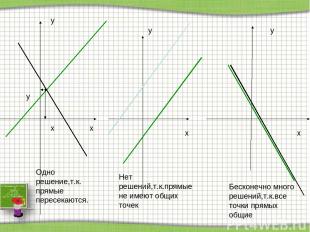
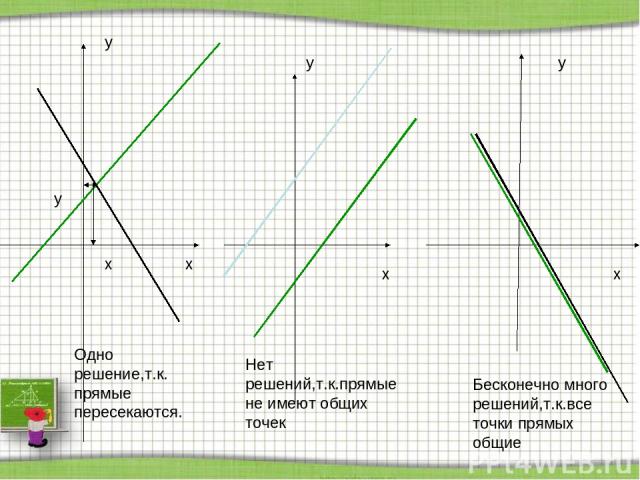
x y x y x y x y Бесконечно много решений,т.к.все точки прямых общие Нет решений,т.к.прямые не имеют общих точек Одно решение,т.к. прямые пересекаются.

Достоинство графического способа –наглядность. Недостаток графического способа– приближённые значения переменных Если система уравнений не имеет решений, то она называется несовместной. Если система уравнений имеет бесконечно много решений, то она называется неопределённой

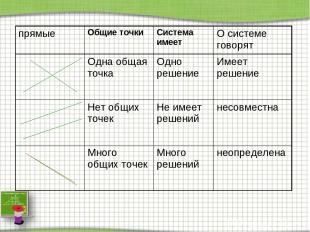
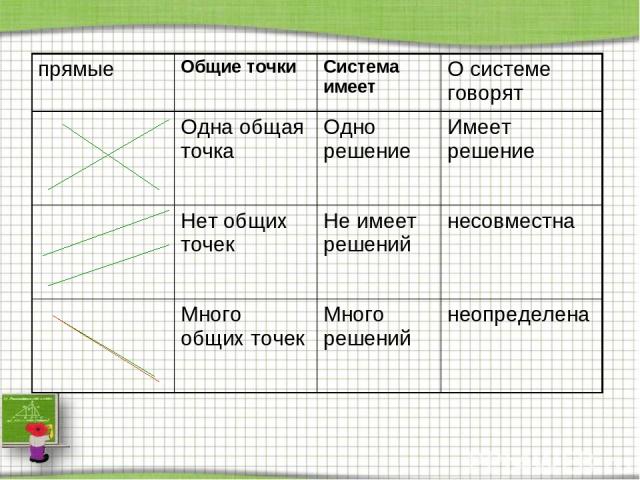
прямые Общие точки Система имеет О системе говорят Одна общая точка Одно решение Имеет решение Нет общих точек Не имеет решений несовместна Много общих точек Много решений неопределена

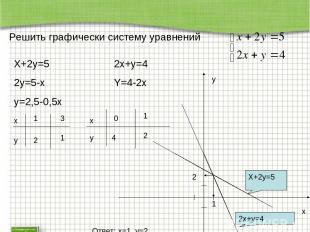
Решить графически систему уравнений X+2y=5 2y=5-x y=2,5-0,5x x y 1 2 3 1 2x+y=4 Y=4-2x x y 0 4 1 2 x y 1 2 X+2y=5 2x+y=4 Ответ: x=1, y=2.

Формулы Крамера ∆---- главный определитель вспомогательные определители ∆ = a1 b1 a2 b2 =a1*b2 –a2*b1 = C1 b1 C2 b2 =c1*b2 –c2*b1 = A1 c1 A2 c2 =a1*c2 –a2*с1 x x 1.Если главный определитель не равен нулю, то система имеет одно решение. 2.Если главный определитель равен нулю, то: Нет решений, если вспомогательные определители не равны нулю; Много решений, если вспомогательные определители равны нулю

Решить систему по формулам Крамера 2 2 1 =1*1-2*2=-3≠0 5 2 4 1 =5*1-4*2=-3 1 5 2 4 =1*4-2*5=-6 =-3 ; (-3) =1 -6 : (-3) =2 Ответ: (1;2)

Метод подбора 1. Назови решение системы уравнений: 2.К уравнению x+y=6 добавь такое уравнение, чтобы решением системы была упорядоченная пара чисел (4;2) 3. Придумать систему уравнений такую, чтобы её решением была упорядоченная пара чисел (5;2)

О количестве решений системы уравнений по виду системы Одно решение Одно решение

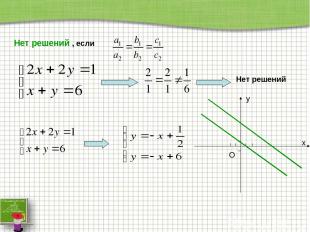
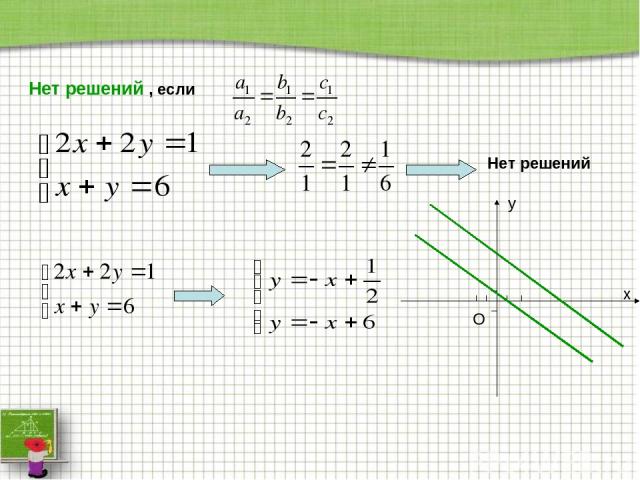
Нет решений , если Нет решений x y О

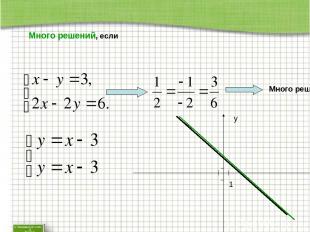
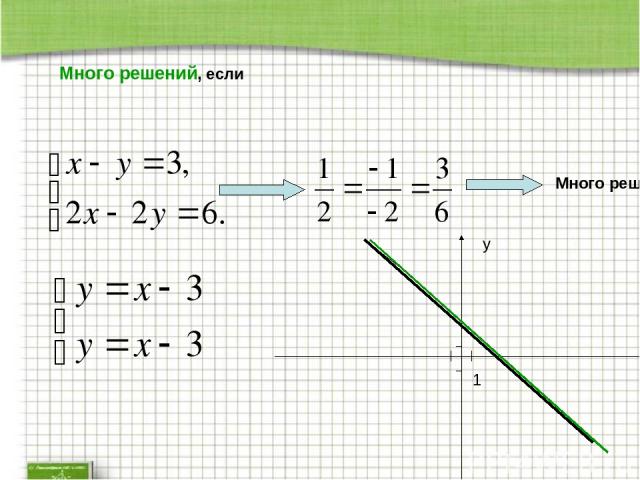
Много решений, если Много решений 1 x y

Проверь себя ( работа в группах) При каком значении параметра система уравнений имеет одно решение? При каком значении параметра система уравнений не имеет решений?

При каком значении параметра система уравнений имеет много решений? Решение: Система имеет много решений, если 4a-4=3a; 4a-3a=4; a=4 Значит при a=4 и Так как То при a=4 система имеет много решений

Итак, мы научились: 1.Решать системы линейных уравнений разными способами; 2.По виду системы отвечать на вопрос: «сколько решений имеет система» 3.А также узнали, при каком условии прямые параллельны, пересекаются.

Зачётная работа по теме: «Решение систем линейных уравнений» Решить систему разными способами(3балла за каждый способ) 2.Решить систему уравнений методом подбора(1 балл)

3. При всех значениях параметра a, определите число решений системы (3балла): 4.При каком значении параметра a система имеет единственное решение (2 балла): 5.При каком значении параметра a система не совместна ( 2 балла):

6.При каком значении параметра a система уравнений неопределена (2 балла): 7. Прямая y=kx+b проходит через точки A(2;7) и B(-1;-2).Найдите значения k и b.(2 балла) Шкала оценивания: 20б-24б --- «5» ; 13б –15б --- «4» ; 6б-9б--- «3»