Презентация на тему: Решение неравенств с двумя переменными

Урок алгебры 9 класс учитель математики Бичурина Надежда Фёдоровна 5klass.net

На предыдущих уроках мы решали системы уравнений графическим способом, системы уравнений аналитическим способом. Сегодня мы переходим к изучению новой темы «Решение неравенств с двумя переменными».Но сначала повторим, как вы усвоили материал прошлого урока. Для этого вспомним графики функций, которые вы изучали.

У=Х2 У=3Х +5 У=Х3 У2+Х2=9 ХУ=8 У=-2Х (Х-2)2+(У+3)2=16

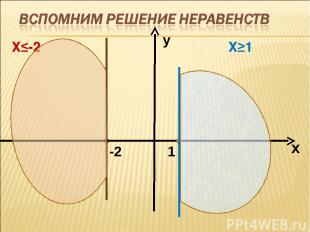
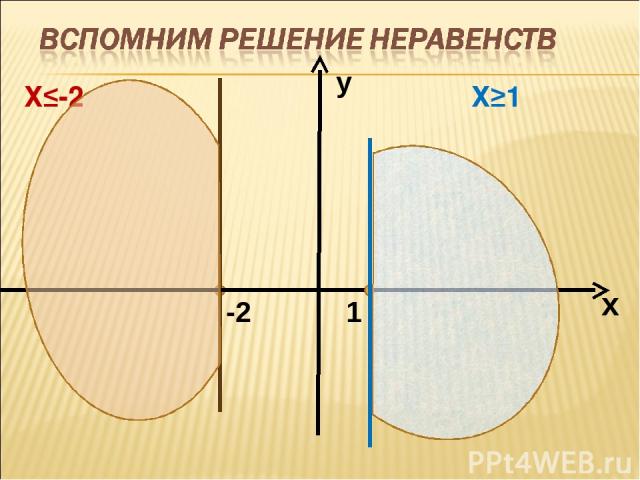
Х≤-2 Х≥1 1 -2 х у

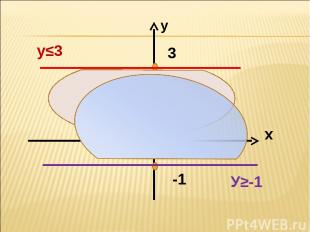
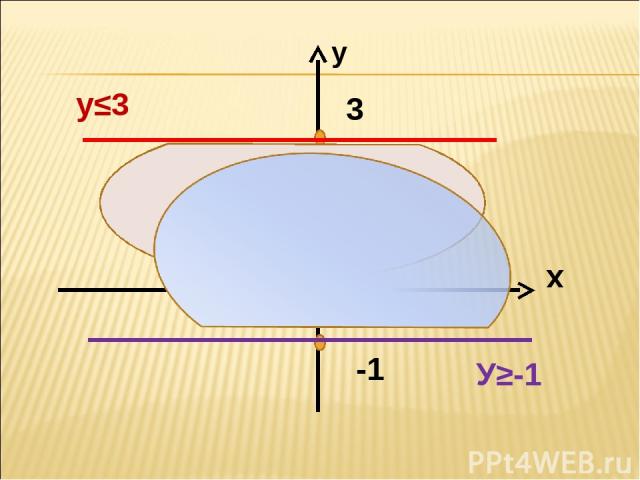
-1 3 у у≤3 У≥-1 х

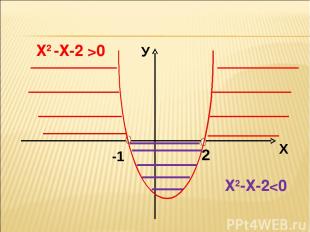
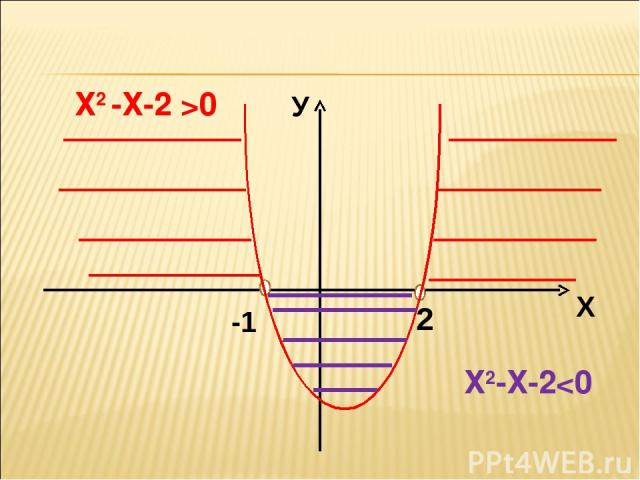
Х2 -Х-2 >0 Х2-Х-2

Ввести понятие неравенств с двумя переменными Составить алгоритм решения неравенств Формировать навыки решения неравенств

Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство.

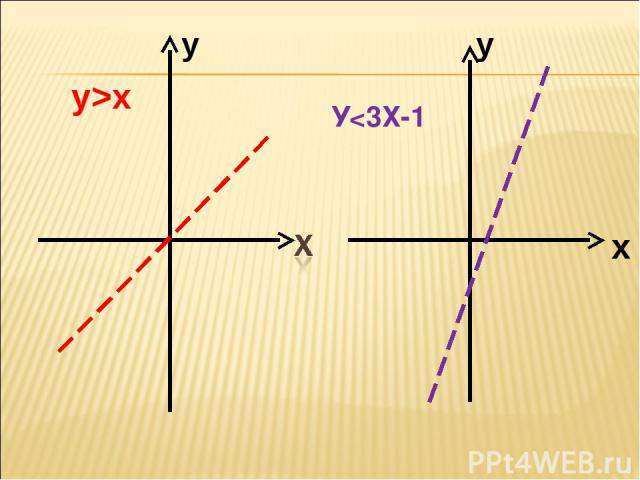
Подберем пару чисел, которая будет являться решением неравенства с двумя переменными. Построить в тетради графики функций У > Х У < 3Х -1 Проверьте, будет ли являться решением неравенства пара чисел (1;3) (-2;-5) (5;-4)?

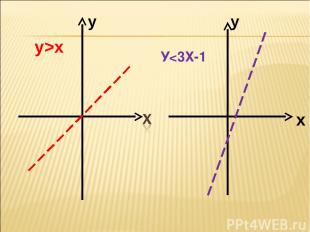
Ух

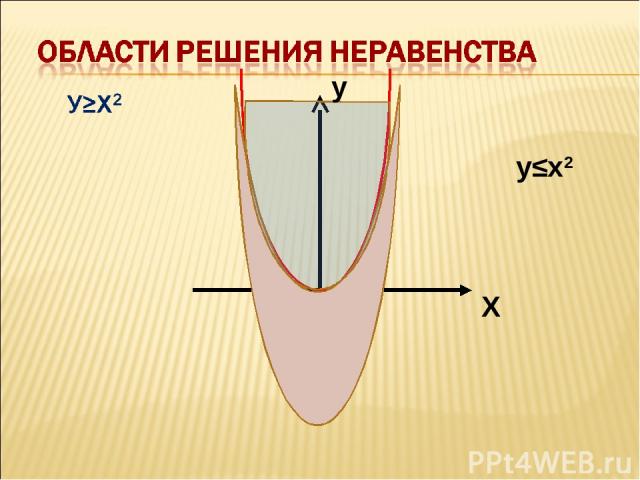
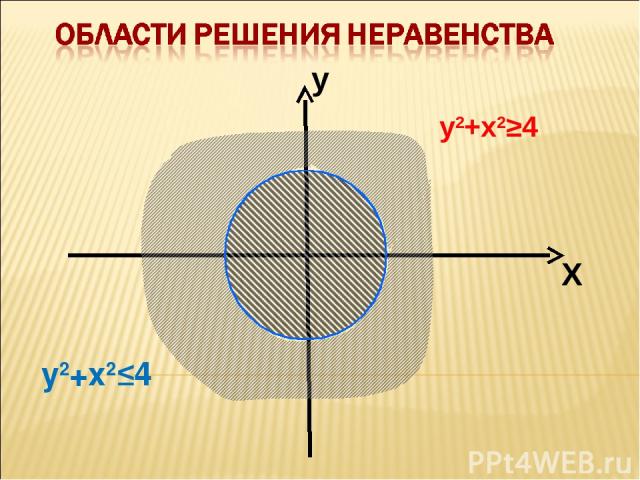
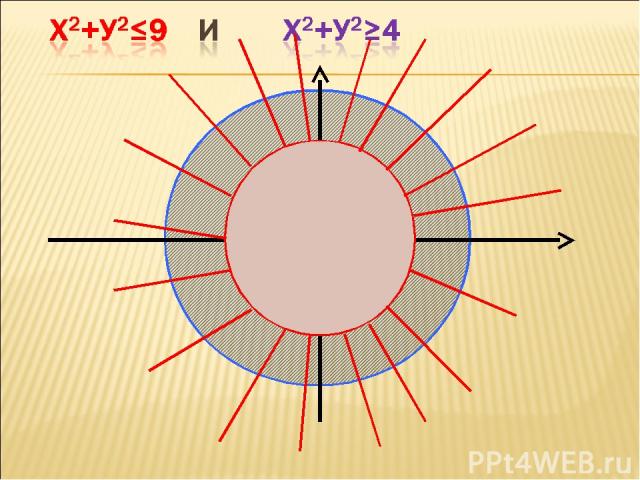
А если даны неравенства вида У > Х2 или У < Х2 х2+у2 < 4 х2+у2 > 4 Как поступить? Выслушать предложения учеников. Ученики самостоятельно предлагают алгоритм решения неравенств.

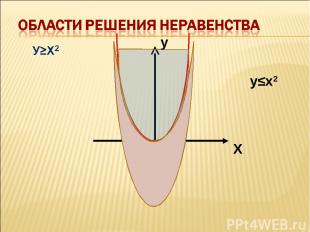
у≤х2 Х у

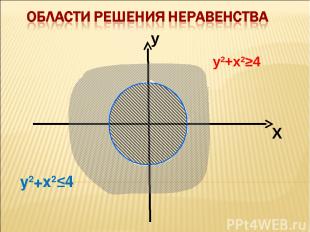
у2+х2≤4 у2+х2≥4 у Х

1. Построить F(x;y)=0 2.Взяв из каждой области пробную точку установить, являются ли ее координаты решением неравенства. 3.Показать область решения неравенства.

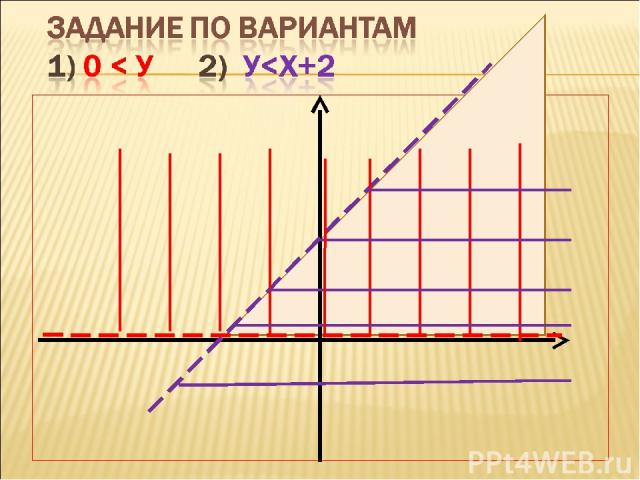
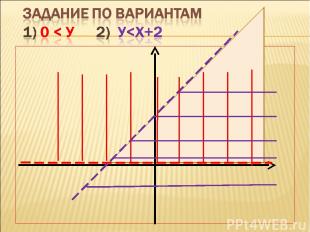
1) 0 < У 2) У

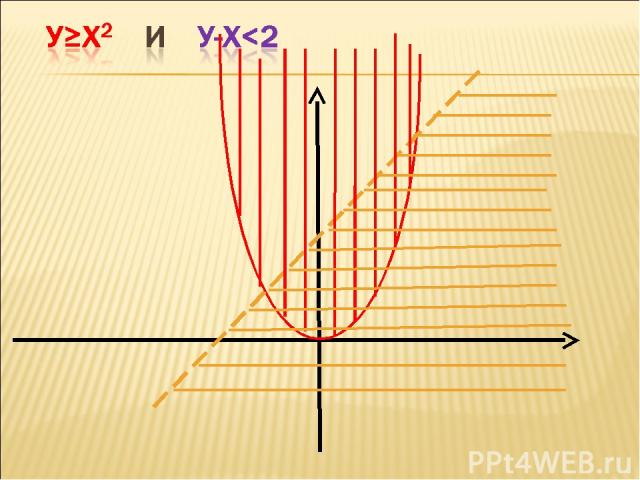
Сначала ребята пробуют самостоятельно решить неравенства. Затем представитель от каждого варианта идет к доске и на одной координатной плоскости показывает решение своего неравенства. Что мы сейчас решили? Учащиеся могут догадаться, что решали систему неравенств.

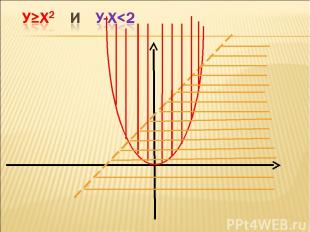
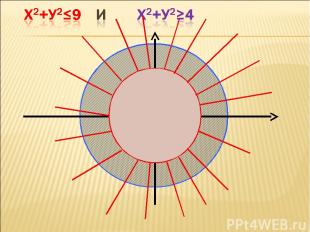
Задание дано одно всему ряду обучающихся, можно совещаться, работая парами, можно консультироваться с учителем. От каждого ряда ученик по желанию на доске показывает и объясняет решение неравенства

1 2 У>2Х-1 У|Х| ХУ≥-10

1.Придумать свое неравенство и изобразить на координатной плоскости множество его решений. Два разных задания. 2.Построить в одной координатной плоскости множество решений неравенств 0 ≤ У У ≤ -Х+2 У ≤ Х+2 Найти площадь и периметр полученной фигуры.