Презентация на тему: Решение иррациональных уравнений

Выполнила Обухова А.А. ученица 8’’Б’’ класса школы № 89 2007 год. 5klass.net

оглавление Определение Основной метод решения иррациональных уравнений Посторонний корень иррационального уравнения Способы обнаружения постороннего корня Алгоритм решения иррациональных уравнений Метод подбора (метод пристального взгляда). Алгоритм решения методом подбора. Определение равносильных уравнений. Равносильные преобразования уравнений Неравносильные преобразования уравнения выход

Определение Иррациональное уравнение – это уравнение, в котором содержится переменная под знаком квадратного корня. Пример: оглавление далее

Основной метод решения иррациональных уравнений - это метод возведения в квадрат обеих частей уравнения. оглавление далее назад

Посторонний корень иррационального уравнения При возведении в квадрат, получаем посторонние корни. x=1 в предыдущем уравнении посторонний корень, т.к. если подставить его в данное иррациональное уравнение, получим Ответ: уравнение не имеет корней. оглавление далее назад

Способы обнаружения постороннего корня Проверка – подстановка полученных корней в иррациональное уравнение. 2. По области допустимых значений – ОДЗ. оглавление далее назад

Пример: Решить иррациональное уравнение: оглавление далее назад

Решение: Найдём корни уравнения по обратной теореме Виета: ОДЗ: оглавление далее назад

Проверка 1 способ: 2 способ: неверно неверно не удовлетворяет ОДЗ. не удовлетворяет ОДЗ. Ответ: уравнение не имеет корней. оглавление далее назад

Алгоритм решения иррациональных уравнений: Область допустимых значений. Возвести в квадрат. Решить рациональное уравнение. Проверить, удовлетворяют ли корни уравнения ОДЗ (или подставить полученные корни в уравнение). Отсеять посторонние корни. оглавление далее назад

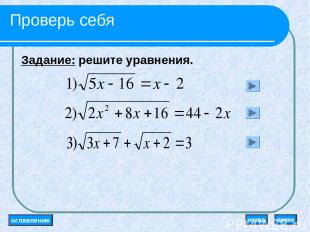
Проверь себя Задание: решите уравнения. оглавление далее назад

Ответы: ОДЗ: Найдём корни уравнения по обратной теореме Виета: удовлетворяет ОДЗ удовлетворяет ОДЗ Ответ: 4; 5. оглавление далее назад

Ответы: Найдём корни уравнения по обратной теореме Виета: Проверка: Выражение не имеет смысла. Ответ: 12. оглавление далее назад

Ответы: оглавление далее назад

Ответы (продолжение): Найдём корни уравнения по обратной теореме Виета: Проверка: Уравнение не имеет смысла. Ответ: -1. оглавление далее назад

Метод подбора (метод пристального взгляда). Сумма двух монотонно возрастающих функций есть функция монотонно возрастающая на области определения, то функция принимает каждое своё значение один раз, значит других корней уравнение не имеет. оглавление далее назад Уравнение 3 решено путем двукратного возведения в квадрат. Познакомимся с другим методом его решения

Алгоритм решения методом подбора: 1. Доказать, что других корней нет, или доказать, что их несколько. 2. Угадать (подобрать) один или несколько корней уравнения. оглавление далее назад

Примеры на метод подбора: Задание: решите уравнения. решение (x=1); решение (уравнение не имеет корней) оглавление далее назад

Определение равносильных уравнений. Два уравнения f(x)=g(x) и r(x)=s(x) называются равносильными, если они имеют одинаковые корни (или, в частности, если оба уравнения не имеют корней). Обычно при решении уравнения стараются заменить данное уравнение более простым, но равносильным ему. Такую замену называют равносильным преобразованием уравнения. оглавление далее назад

Равносильные преобразования уравнений Перенос членов уравнения из одной части уравнения в другую с противоположным знаком. 2x + 5 = 7x – 8; уравнения равносильны 2x -7x = - 8 – 5. оглавление далее назад

Равносильные преобразования уравнений (продолжение) Умножение или деление обеих частей уравнения на одно и то же отличное от нуля число. оглавление далее назад

Неравносильные преобразования уравнения 1. Освобождение от знаменателей, содержащих переменные т.к. x2 = 4 имеет два корня -2; и 2. Посторонний корень – 2. 2. Возведение обеих частей уравнения в квадрат. оглавление выход назад