Презентация на тему: Решение иррациональных уравнений и неравенств

Орловой Анастасии IV курс 3 группа 900igr.net

Цели обучения теме Тематическое планирование Логико-математический анализ темы Анализ задачного материала Пример работы с понятием Пример работы с теоремой Пример работы с задачей Дополнительные задачи Система контроля Использованная литература

Назад

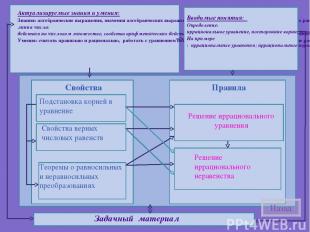
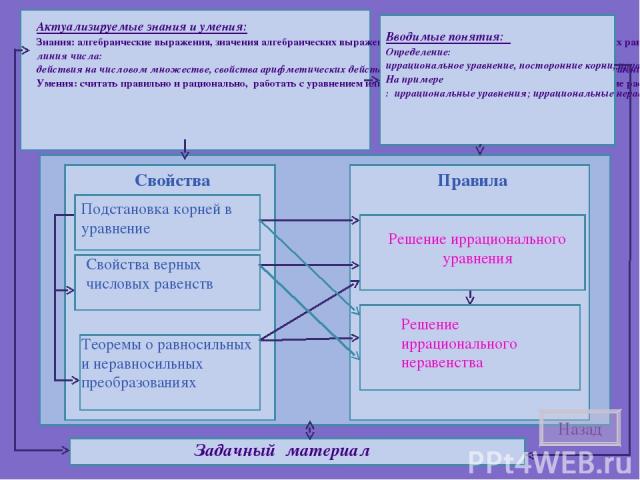
Подстановка корней в уравнение Свойства верных числовых равенств Теоремы о равносильных и неравносильных преобразованиях Решение иррационального уравнения Решение иррационального неравенства Назад

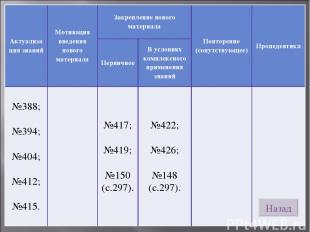
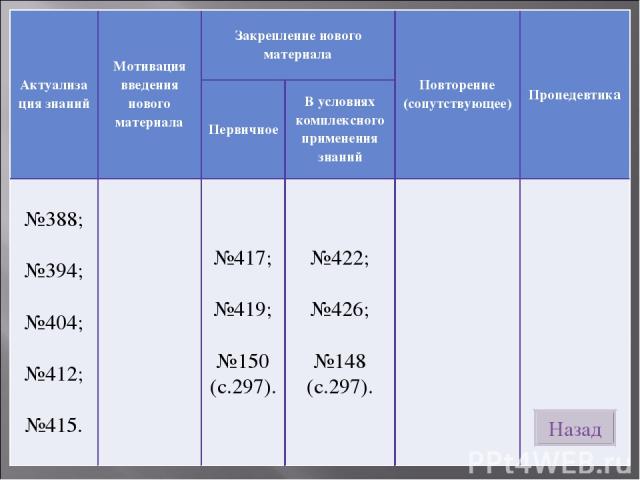
Назад Актуализация знаний Мотивация введения нового материала Закрепление нового материала Повторение (сопутствующее) Пропедевтика Первичное В условиях комплексного применения знаний №388; №394; №404; №412; №415. №417; №419; №150 (с.297). №422; №426; №148 (с.297).

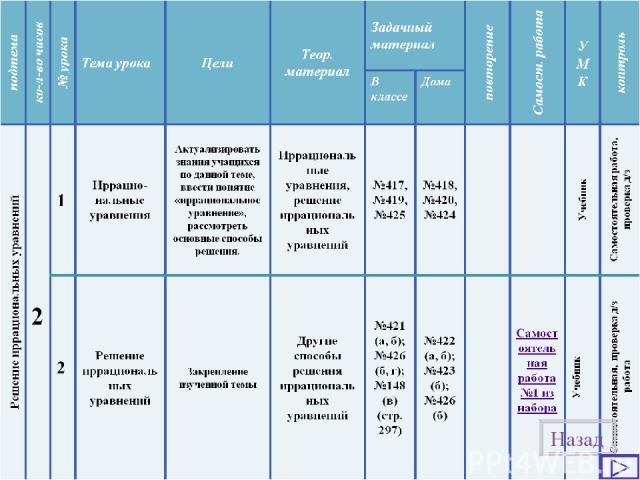
Назад

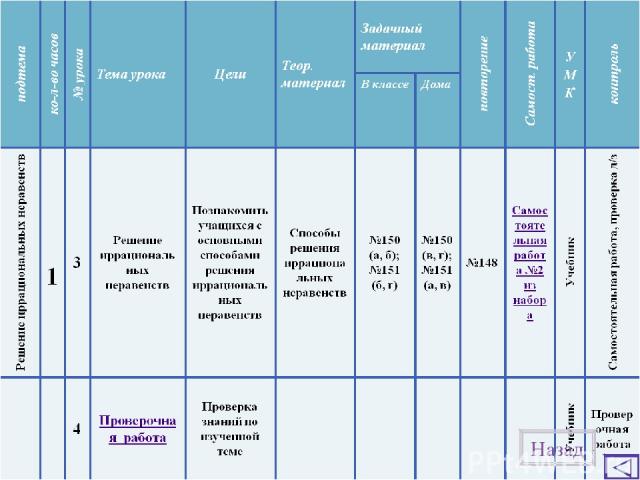
Назад

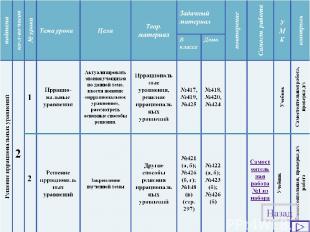
Набор задач по теме «иррациональные уравнения» Первый уровень: Назад

Набор задач по теме «иррациональные уравнения» Второй уровень: Назад

Набор задач по теме «иррациональные уравнения» Третий уровень: Назад

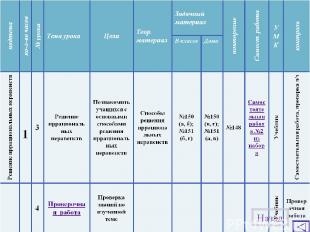
Набор задач по теме «иррациональные неравенства» Первый уровень: Назад

Набор задач по теме «иррациональные неравенства» Второй уровень: Назад

Набор задач по теме «иррациональные неравенства» Третий уровень: Назад

Назад Понятие «иррациональное уравнение» Учащимся даётся карточка с заданием, в котором пропущены некоторые слова. Задача учащихся – заполнить все пропуски к концу урока.

Назад   Определение. Уравнение, в котором переменная содержится _________________________(или под знаком операции возведения в дробную степень), называется иррациональным.  Примеры:  Основные свойства:  1. Все корни четной степени, входящие в уравнение, являются арифметическими. а) Если подкоренное выражение положительно, то значение корня ___________ б) Если подкоренное выражение равно нулю, то значение корня ______________ в) Если подкоренное выражение отрицательно, то значение корня ____________ 2. Все корни нечетной степени, входящие в уравнение, определены при любом действительном значении подкоренного выражения. а) Если подкоренное выражение положительно, то значение корня __________ б) Если подкоренное выражение равно нулю, то значение корня _____________ в) Если подкоренное выражение отрицательно, то значение корня ___________ Посторонний корень иррационального уравнения – это _____________________________________

Назад Актуализация знаний: Вспоминаются свойства степени и арифметического квадратного корня Найдите значение выражения:

Назад 2) При каких значениях а верно равенство: 3) Вынесите множитель из-под знака корня

Назад 4) Внесите множитель под знак корня 5) Освободитесь от иррациональности в знаменателе

Назад На доске выписаны иррациональные уравнения, задание – выделить общие черты этих уравнений, после чего сформулировать определение иррационального уравнения.

Назад Иррациональное уравнение – это уравнение, в котором переменная содержится под знаком корня

Назад После заполнения карточки в конце урока для закрепления из приведённого ниже списка уравнений выбрать те, которые являются иррациональными

Назад Работа с задачей Уравнение: Так как изучение темы проводится в рамках проблемного обучения, то ученики должны сами «открыть» способ решения этого уравнения. Для этого можно предложить набор уравнений с возрастающей сложностью, с помощью решения которых ученики смогут понять, как решать иррациональные уравнения

Назад

Назад

Назад

Назад Так, на основе вспомогательных задач, учащиеся сами «открывают» способы решения иррациональных уравнений, так как знания получены самостоятельно, они лучше усваиваются. Так же ученики выписывают основные методы решения уравнений, обосновывают необходимость проверки при решении.

Работа с теоремой Теорема. Если от обеих частей уравнения взять одну и ту же немонотонную функцию, которая не изменяет ОДЗ уравнения, то новое уравнение может содержать лишние корни, которые будут входить в ОДЗ исходного уравнения, и поэтому при таком способе решения каждое из найденных решений надо проверить непосредственной подстановкой в исходное уравнение. Причём эту проверку довести до численного равенства. Назад

В данном случае, рассматривается возведение в квадрат или любую другую чётную степень. Рассматриваются два примера: 1) Решая это уравнение, получаем единственное решение x = 5, однако при подстановке в уравнение мы не получим верного равенства. х = 5 - посторонний корень уравнения. Заметим, что x = 5 не входит в ОДЗ исходнго уравнения. Значит ли это, что при решении любого уравнения мы должны находить его ОДЗ? Назад

Рассмотрим второе уравнение: При решении этого уравнения получаем два корня х = 5 и х = 197. Оба корня входят в ОДЗ исходного уравнения, однако при подстановке в исходное уравнение, оказывается, что х = 197 не является корнем исходного уравнения. х = 197 – посторонний корень. В результате учащиеся должны сделать вывод о том, что при решении иррациональных уравнений необходимо делать проверку, даже если корни входят в ОДЗ. Назад

Далее ставится вопрос о том, откуда возникают посторонние корни. - это исходное уравнение. При возведении обеих его частей в квадрат, получим Но корнями этого уравнения буду так же корни уравнения Которые могут и не являться корнями исходного уравнения. Назад

Эти корни будут посторонними. Для того, чтобы их не включить в ответ, и нужна проверка. Назад

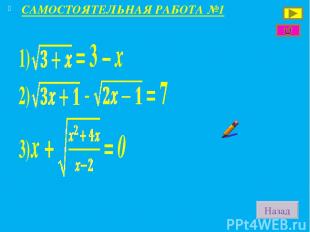
САМОСТОЯТЕЛЬНАЯ РАБОТА №1 Назад

САМОСТОЯТЕЛЬНАЯ РАБОТА №2 Назад

КОНТРОЛЬНАЯ РАБОТА Назад

Актуализируемые знания и умения: Знания: алгебраические выражения, значения алгебраических выражений, алгебраические равенства, свойства числовых равенств, правила раскрытия скобок; линия числа: действия на числовом множестве, свойства арифметических действий; понятие уравнения, неравенства, приёмы решения уравнений и неравенств Умения: считать правильно и рационально, работать с уравнением или неравенством, проводить простейшие логические рассуждения. Назад

Вводимые понятия: Определения: иррациональное уравнение, посторонние корни, иррациональное неравенство, На примере: иррациональные уравнения; иррациональные неравенства, способы решения иррациональных уравнений и неравенств Назад

Алгебра и начала анализа 10-11. под ред. А.Н.Колмогорова, Москва, Просвещение, 2001г. «Математика для поступающих в вузы», Москва, «Дрофа», 1997 г. «Математика. Справочник школьника», Якушева Г., «Слово», 1997 г «Математика. Справочные материалы», В.А.Гусев, А.Г. Мордкович, Москва, «Просвещение», 1988 г. «Математика. Наглядный справочник с примерами», Л.Э.Генденштейн, Москва, «ИЛЕКСА», 2005г. Назад