Презентация на тему: Решение рациональных уравнений

Тема: Первые представления о решении рациональных уравнений. Цель урока: систематизация и обобщение знаний о выполнении действий с алгебраическими дробями, решении уравнений и задач, математическая модель которых представляет рациональное выражение. 900igr.net

Теоретический тест: Действия с алгебраическими дробями.

2. Основное свойство алгебраической дроби: а) И числитель, и знаменатель дроби можно умножить или разделить на одно и то же число. Приведение к новому знаменателю. Сокращение дроби б) И числитель, и знаменатель алгебраической дроби можно умножить или разделить на один и тот же многочлен. Приведение к новому знаменателю. Сокращение алгебраической дроби

3. Алгоритм сложения (вычитания) алгебраических дробей. а) Найти для каждой дроби новый числитель. 1 б) Найти дополнительные множители для каждой 2 дроби. в) Разложить все знаменатели на множители. 3 г) Выполнить сложение ( вычитание) полученных 4 дробей. д) Составить общий (новый) знаменатель. 5 е) В числителе привести подобные слагаемые. 6 ж) Проверить полученную дробь. 7

4. Переменные, входящие в состав алгебраической дроби, принимают лишь допустимые значения, при которых а) знаменатель дроби не обращается в нуль. б) знаменатель и числитель дроби не обращается в нуль. в) числитель дроби не обращается в нуль.

5) Условие равенства дроби нулю: а)А(х) = 0 В(х) 0 б)А(х) =0 В(х) = 0 в)А(х) = 0

Способы разложения на множители 1.Распределительный закон. АС+ВС=С(А+В)

Способы разложения на множители. 2.Способ группировки. an+bn+am+bm= =n(a+b)+m(a+b)= =(a+b)(n+m).

Способы разложения на множители. 3.Формулы сокращенного умножения.

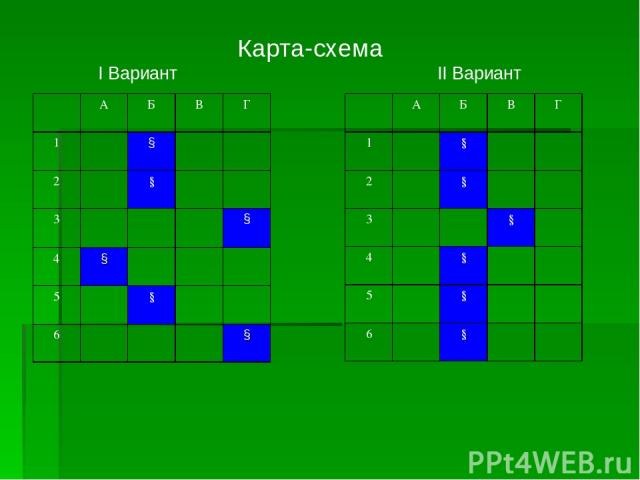
Тематический тест. Действия с алгебраическими дробями. «Морской бой»
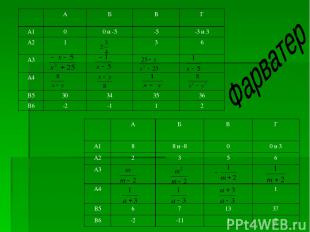
А Б В Г А1 0 0 и -5 -5 -3 и 3 А2 1 3 6 А3 А4 В5 30 34 35 36 В6 -2 -1 1 2 А Б В Г А1 8 8 и -8 0 0 и 3 А2 2 3 5 6 А3 А4 1 В5 6 7 13 37 В6 -2 -11 1 2
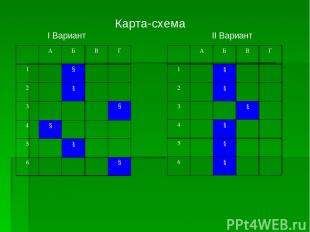
Карта-схема I Вариант II Вариант А Б В Г 1 § 2 § 3 § 4 § 5 § 6 § А Б В Г 1 § 2 § 3 § 4 § 5 § 6 §