Презентация на тему: Решение показательных неравенств

Урок – лекция по теме : «Показательные неравенства, их типы и методы решения» Учитель математики МОУ – СОШ №2 р.п.Степное Труфякова Галина Ивановна 900igr.net

Аннотация урока Тема « Показательные неравенства» является важнейшей темой математики . По учебнику С. М. Никольского она изучается в 10 классе и на её изучение по планированию отводится 2 часа : 1час-Простейшие показательные неравенства ; 1 час – Неравенства , сводящиеся к простейшим заменой неизвестного . За это время нужно познакомить учащихся с новым и очень объёмным материалом , научить их решать все типы показательных неравенств и хорошо отработать эти навыки и умения .Поэтому уроки формирования новых знаний в виде лекций с применением информационно-коммуникационной технологии позволяют решать эти проблемы быстро и с большим успехом .

Альберт Эйнштейн « Мне приходится делить своё время между политикой и решением уравнений и неравенств . Однако решение уравнений и неравенств , по-моему, гораздо важнее , потому что политика существует только для данного момента , а уравнения и неравенства будут существовать вечно .»

Структура урока Организационный момент Постановка целей и задач План лекции Актуализация знаний учащихся в виде повторения ранее изученного материала Введение новых знаний Закрепление знаний в форме собеседования Подведение итогов урока Домашнее задание

Организационный момент Приветствовать учащихся Отметить в классном журнале фамилии учащихся , отсутствующих на уроке

Постановка целей и задач Объявить учащимся в начале урока его цели и задачи Познакомить учащихся с планом лекции и записать его в тетради

Цели урока Образовательные Формирование понятия показательного неравенства Ознакомление учащихся с типами показательных неравенств Формирование умений и навыков решения показательных неравенств

Цели урока Воспитательные Воспитание трудолюбия Воспитание самостоятельности в достижении цели Формирование вычислительных навыков Формирование эстетических навыков при оформлении записей

Цели урока Развивающие Развитие мыслительной деятельности Развитие творческой инициативы Развитие познавательной активности Развитие речи и памяти

Задачи урока Повторить свойства показательной функции Повторить правила решения квадратных и дробно – рациональных неравенств Отработать алгоритм решения простейших показательных неравенств Научить учащихся различать типы показательных неравенств Научить учащихся решать показательные неравенства

Тип урока Урок формирования новых знаний

Вид урока Урок - лекция

Методы обучения Объяснительно-иллюстративный Эвристический Поисковый Проблемный

Технология обучения Информационно-коммуникационная технология, основанная на проблемном обучении

План лекции Повторение свойств показательной функции Простейшие показательные неравенства Показательные неравенства, сводящиеся к простейшим Показательные неравенства, сводящиеся к квадратным неравенствам Однородные показательные неравенства первой степени Однородные показательные неравенства второй степени Показательные неравенства, сводящиеся к рациональным неравенствам Показательные нестандартные неравенства

Повторение ранее изученного материала Решить на доске и в тетрадях : а) квадратные неравенства : х² – 2х – 1 ≥ 0 х² – 2х - 3 ≤ 0 б) дробно- рациональное неравенство : ( х – 5) \ ( х - 2 ) ≤ 0

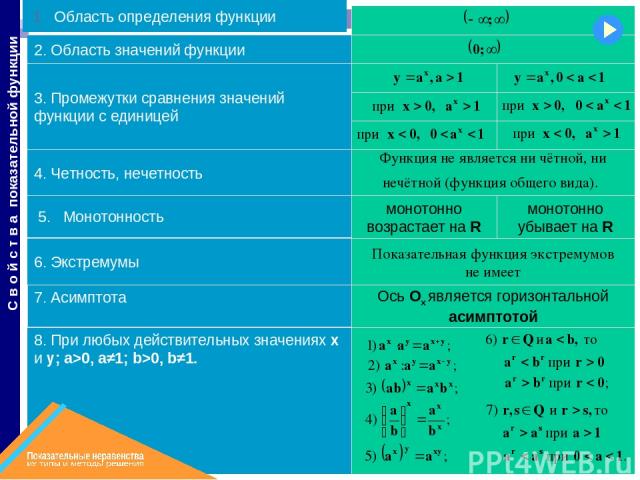
Повторение свойств показательной функции

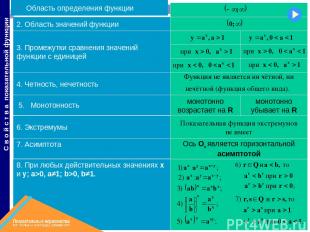
монотонно убывает на R Ось Ох является горизонтальной асимптотой монотонно возрастает на R 8. При любых действительных значениях х и у; a>0, a≠1; b>0, b≠1. 7. Асимптота 6. Экстремумы 5. Монотонность 4. Четность, нечетность 3. Промежутки сравнения значений функции с единицей 2. Область значений функции 1 Область определения функции С в о й с т в а показательной функции Показательная функция экстремумов не имеет Функция не является ни чётной, ни нечётной (функция общего вида).

возрастающая убывающая возрастающая убывающая

Введение новых знаний

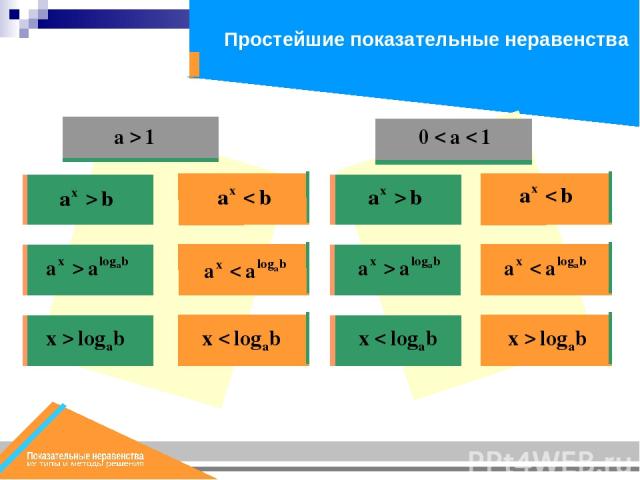
Пусть а – данное положительное, не равное единице число и b – данное действительное число. Тогда неравенства ax > b (ax ≥ b) и ax < b (ax ≤ b) называются простейшими показательными неравенствами.

Решением неравенства с неизвестным х называют число х0, при подстановке которого в неравенство получается верное числовое неравенство.

Решить неравенство – значит, найти все его решения или показать, что их нет.

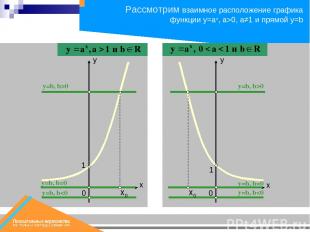
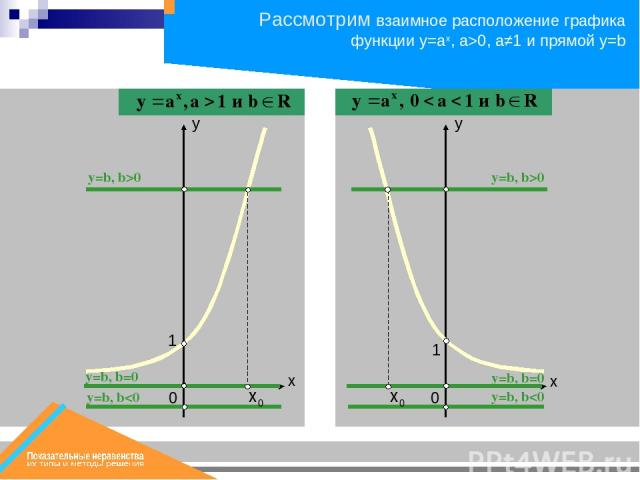
y=b, b0 0 1 0 1 х0 х0

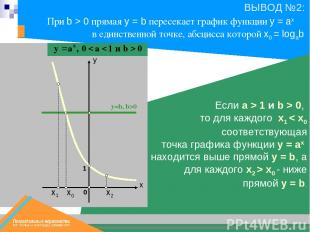
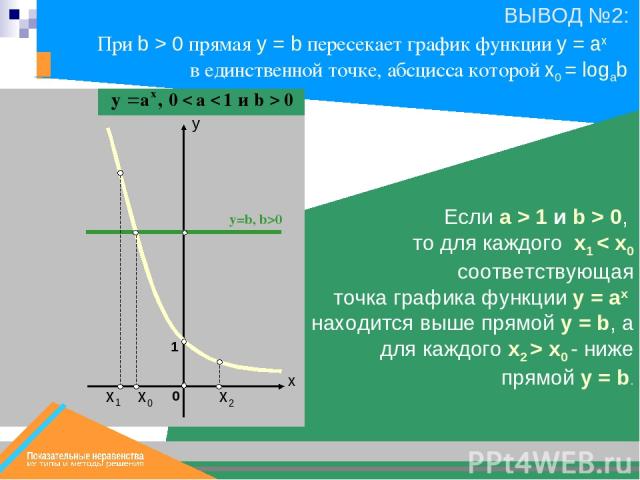
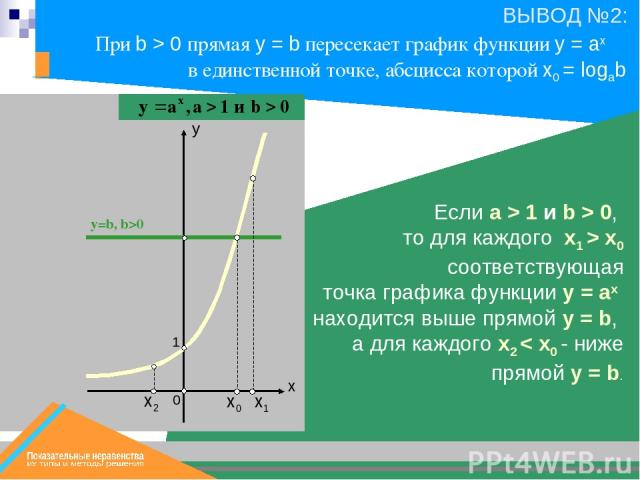
х0 х1 y=b, b>0 х2 Если a > 1 и b > 0, то для каждого x1 < x0 соответствующая точка графика функции y = ax находится выше прямой y = b, а для каждого x2 > x0 - ниже прямой y = b. 1 При b > 0 прямая у = b пересекает график функции y = ax в единственной точке, абсцисса которой x0 = logab

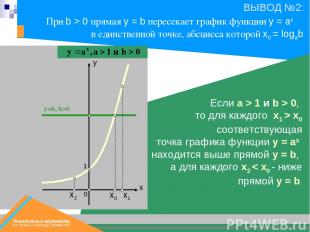
х0 х1 y=b, b>0 1 Если a > 1 и b > 0, то для каждого x1 > x0 соответствующая точка графика функции y = ax находится выше прямой y = b, а для каждого x2 < x0 - ниже прямой y = b. При b > 0 прямая у = b пересекает график функции y = ax в единственной точке, абсцисса которой x0 = logab х2

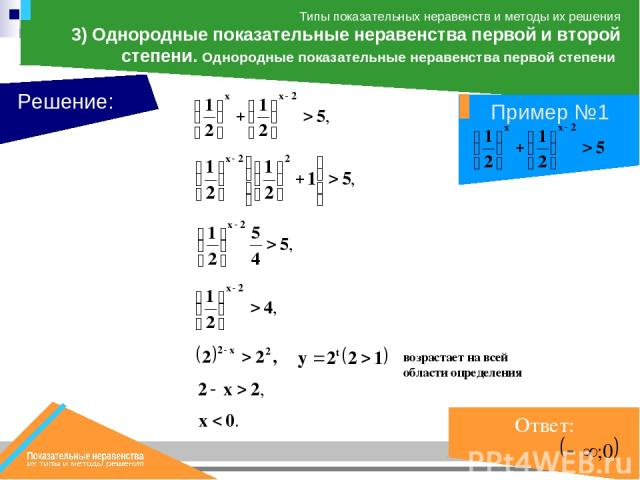
возрастает на всей области определения, Решение:

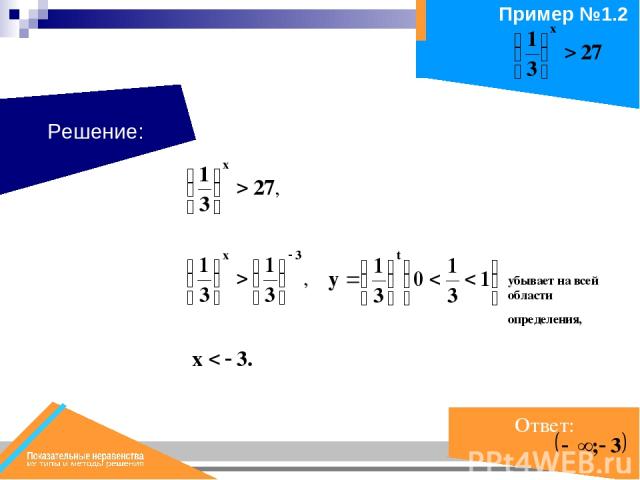
Решение: убывает на всей области определения,

Решение: возрастает на всей области определения,

возрастает на всей области определения

возрастает на всей области определения,

возрастает на всей области определения

Вернёмся к переменной х возрастает при всех х из области определения

возрастает на всей области определения

убывает на всей области определения

Вернёмся к переменной х убывает на всей области определения

Вернёмся к переменной х возрастает на всей области определения

Решим каждое утверждение совокупности отдельно.

Проверка Проверка показала, что х=1, х=3, х=1,5 являются решениями уравнения, а х=2 не является решением уравнения.

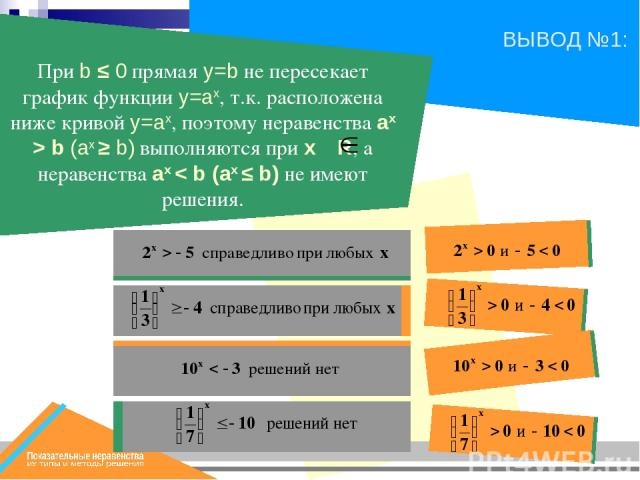
Закрепление знаний Какие неравенства называются показательными ? Когда показательное неравенство имеет решение при любых значениях х ? Когда показательное неравенство не имеет решений ? Какие типы неравенств вы узнали на этом уроке ? Как решаются простейшие неравенства ? Как решаются неравенства , сводящиеся к квадратным ? Как решаются однородные неравенства ? Как решаются неравенства , сводящиеся к рациональным ?

Итог урока Выяснить , что нового узнали учащиеся на этом уроке Выставить оценки учащимся за работу на уроке с подробным комментированием

Домашнее задание Учебник для 10 класса «Алгебра и начала анализа « автор С.М.Никольский Пункты 6.4 и 6.6 изучить , № 6.31-6.35 и № 6.45- 6.50 решить

Спасибо за хорошую работу и внимание !