Презентация на тему: Геометрия 8 класса в одной задаче

Работу выполнила: Катерноза Маргарита Ученица 9 «А» класса Руководитель: Курбатова С.В. Михнево 2012

показать многообразие подходов при решении одной геометрической задачи и найти более рациональный способ решения.

Найти площадь трапеции, основания которой равны 40 см и 20см, а боковые стороны 12 см и 16 см.
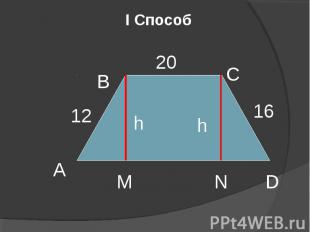
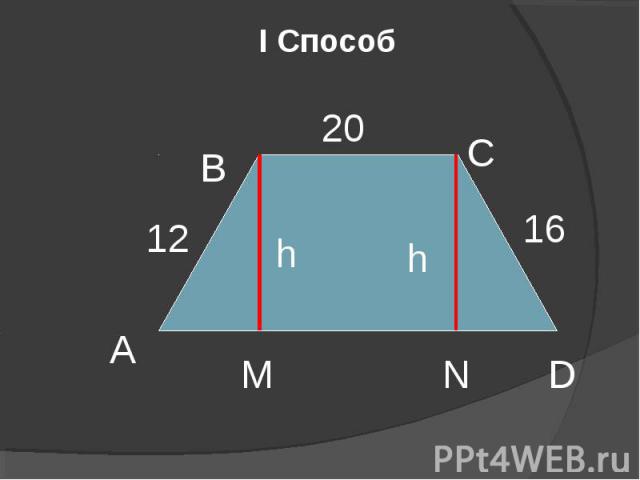
I Способ А М N D С В h h 16 20 12

а S АВСД = Так как S АВСD= ,то задача сводится к нахождению высоты H. Проведем отрезки ВМ и СN так, что ВМ┴АD и СN┴АD, тогда ВСNМ – прямоугольник. Поэтому ВМ = СN и ВС = МN. Но в таком случае АМ + ND =20 Пусть АМ = х (см), тогда ND = 20 – х (см). По теореме Пифагора из ▲АВМ и ▲СND: НІ = 12І - хІ и НІ =16І - (20 – х) І. Составим равенство 12І - хІ = 16І - (20 – х) І, 144 - хІ = 256 – 400 + 40х - хІ , 40х = 288, х = 7,2 (см ). Находим высоту Н: НІ = 12І – 7,2І = 144 – 51,84 = 92,16, Н = Тогда S АВСD= Ответ: 288(смІ)
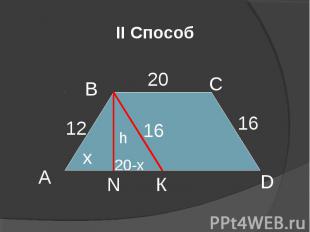
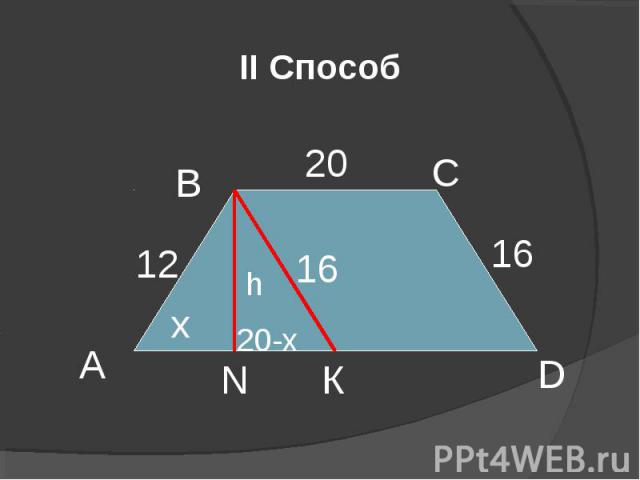
II Способ А D В С К N 20 12 16 х h 20-x 16

Пусть ВN ┴АD и ВК║СD, тогда ВСDК – параллелограмм. Значит ВК = СD = 16 (см), КD = ВС = 20 (см). Пусть АN = х (см), тогда NК = (20 –х) см. Выразим высоту Н из треугольников АВN и ВNК по теореме Пифагора: НІ = 12І - хІ и НІ =16І - (20 – х) І. Составим равенство 12І - хІ = 16І - (20 – х) І, 144 - хІ = 256 – 400 + 40х - хІ , 40х = 288, х = 7,2 (см ). Н = 9,6см. Значит площадь трапеции S АВСD = (смІ). Ответ: 288 смІ
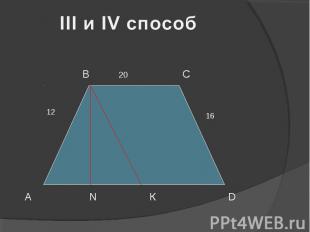
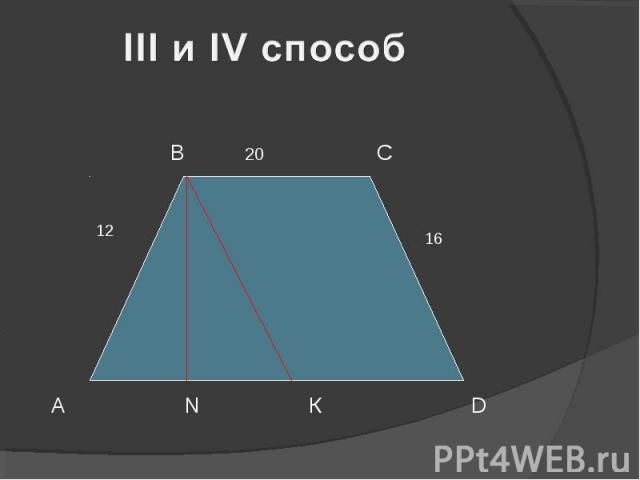
16 В 20 С А N К D 12
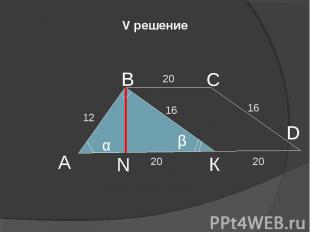
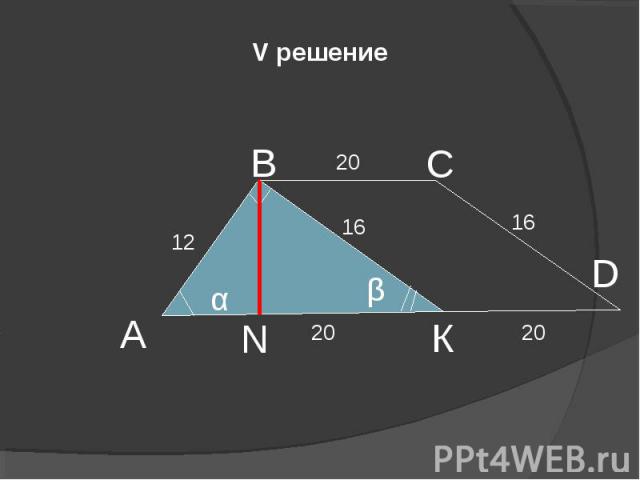
V решение А В К N α β 12 16 C D 20 16 20 20
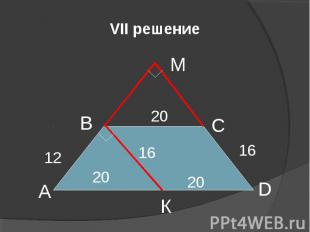
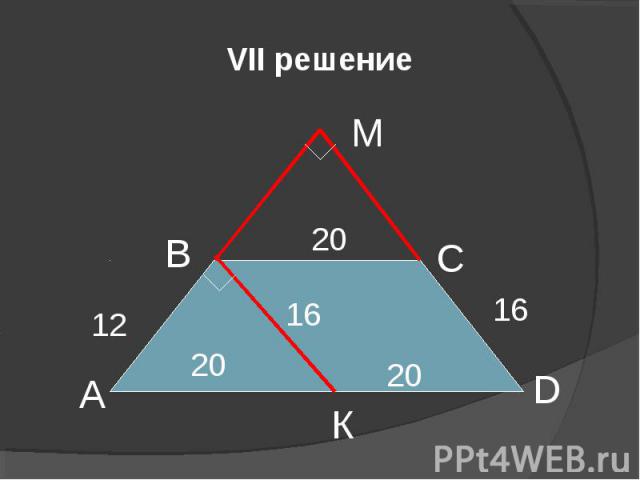
VII решение А В С D М 20 20 16 16 20 12 К
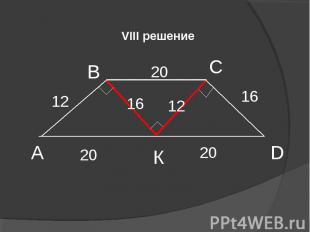
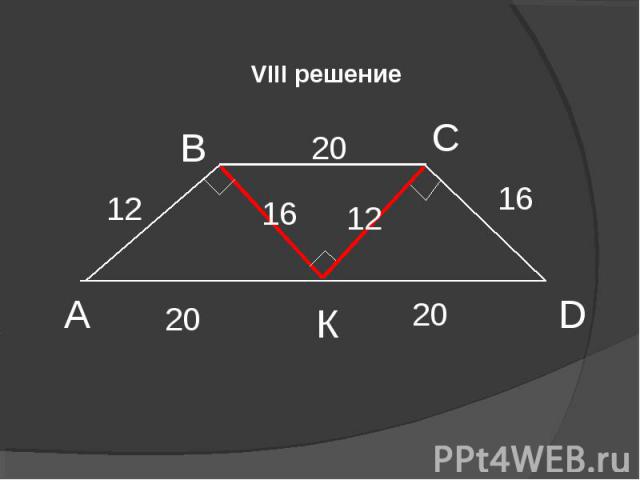
VIII решение А В С D К 12 16 20 16 12 20 20

B C A D M N 20 16 12 40
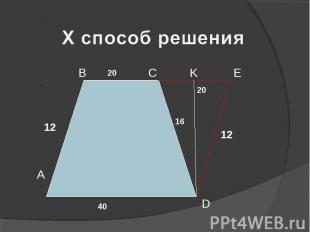
А В С D K E 12 20 20 12 16 40
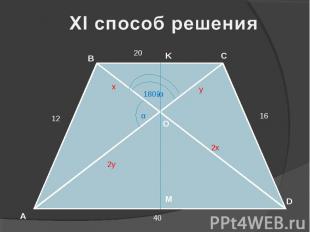
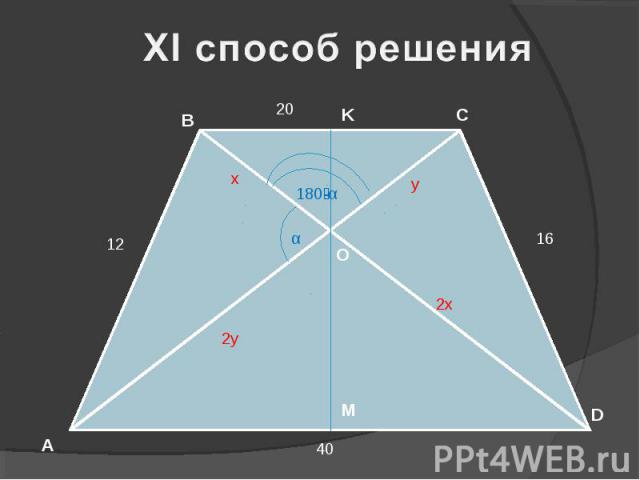
D B C A O 20 K M 12 16 40 x 2x y 2y α 180-α

определение трапеции и формулу нахождения ее площади; свойства прямоугольника и параллелограмма; теорему Пифагора; пропорциональность отрезков в прямоугольном треугольнике; теорему, обратную теореме Пифагора; площадь прямоугольного треугольника; площадь треугольника через основание и высоту; формулу Герона для вычисления площади треугольника; подобие треугольников; теорему об отношении площадей подобных треугольников; тригонометрические зависимости в прямоугольном треугольнике Темы, используемые при решении: