Презентация на тему: Параллельность плоскостей 10 класс

Урок геометрии в 10 классе по теме «Параллельность плоскостей» Учитель математики ГОУ Гимназии № 1579Ягодкина Е.Б.

«Параллельный мир -нечто, состоящее из слов и линий» Помню снов тоску. Тогда перед зеркалом стоял и взгляд находил, растворял. Мысли бились друг о друга.Так, бильярдные шары у вечерней пустоты откалывают штукатурку звуков. Так, будильник-сфинкс равнодушно и угрюмо кожу чувств царапает, глотает. Но в молчанье свой предел. Всполохнутся мошки бликов, солнце-сердце растопит все снега. Это прошлое взбунтует и вздохнет уснувшая мечта.Анатолий Кудрявцев

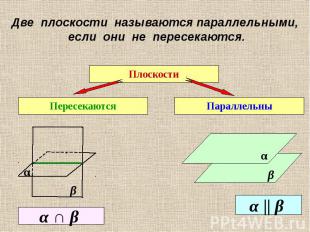
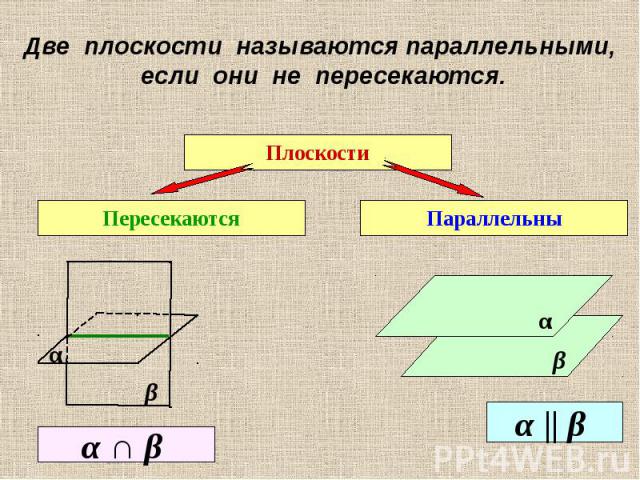
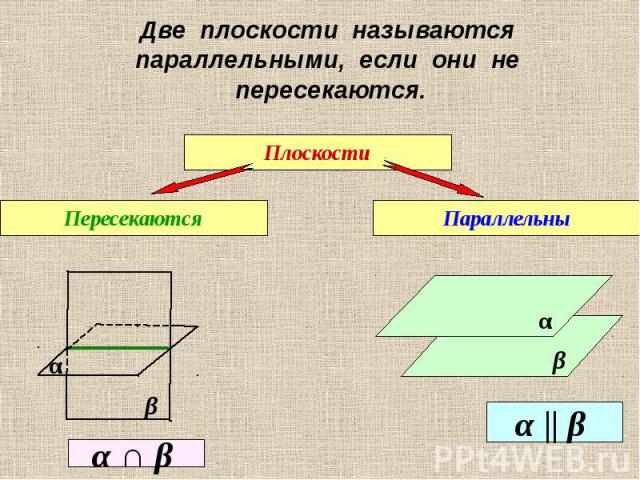
Две плоскости называются параллельными, если они не пересекаются.

Параллельные плоскости в природеЕсли стоять спиной к водопаду, скалы образуют геометрически правильные параллельные плоскости

Параллельные плоскости в техникеПараллельные плоскости «летают»

Параллельные плоскости в быту В своей сущности и основе геометрия –это пространственное воображение, пронизанное и организованное строгой логикой В ней всегда присутствуют эти два неразрывно связанных элемента: наглядная картина и точная формулировка, строгий логический вывод.Там, где нет одной из этих сторон, нет и подлинной геометрии.

Параллельные плоскости в искусствеД.Грин «Мечты» Силуэты мальчика расположены в параллельных плоскостях

Невозможные структуры Жос Де Мей.(Jos de Mey) Жос де Мей (Jos de Mey) родился в 1928 году в Бельгии. Первые его работы были основаны на использовании различных математических законов и последовательностей, таких как ряд Фибоначчи и золотое сечение, но с 1976 года он с особой выразительностью стал использовать обман зрения, наряду с точным воспроизведением материалов и эффекта света и тени. Изображение невозможных фигур как таковых только увеличивает кажущуюся реалистичность.

Невозможные структуры Жос Де Мей.(Jos de Mey) Часто на картинах Жоса де Мея изображена сова.Эта птица в Голландии имеет двоякое значение, с одной стороны – она является символом теоретических знаний, а с другой стороны – совой голландцы называют человека, которые выглядит глупо.

Невозможные фигуры возможны! Речной вокзал в Твери. Кстати, это место, где снимали несколько сцен фильма "Чучело". От этой пристани в финале фильма отходит пароход.Неправильно направленный на объект фотоаппарат сделал параллельные плоскости непараллельными

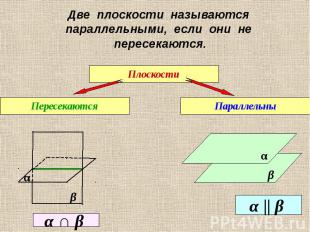
Две плоскости называются параллельными, если они не пересекаются.

Признак параллельности плоскостейЕсли две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. Дано: а α; вα; а∩в=М; а1 β; в1 β; а║а1; в║в1 Доказать, что α || β

Доказательство от противного а α; а1 β; а║а1а║β в α; в1 β; в║в1в║βПусть α ∩ β = сТогда а || β, α ∩ β = с а || с.b || β, α ∩ β = сb || с. а ∩ в=М; а║с; и в║са||b Находим противоречие условию: через точку М проходят две прямые а и b, параллельные прямой с. Предположение α ∩ β = с - неверно

Какие теоремы мы использовали при доказательстве признака?

Задача № 51.(еще один признак параллельности) Дано: т ∩ п = К, т Є α, п Є α, т || β, п || β.Доказать: α || β. 1) Допустим, что ___________ 2) Так как __________________, то ______________________. Получаем, что ______________________________________________________. через точку К проходят две прямые параллельные прямой с.

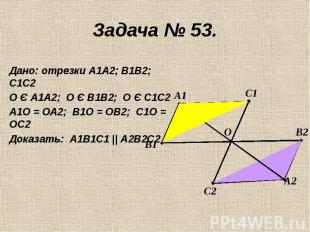
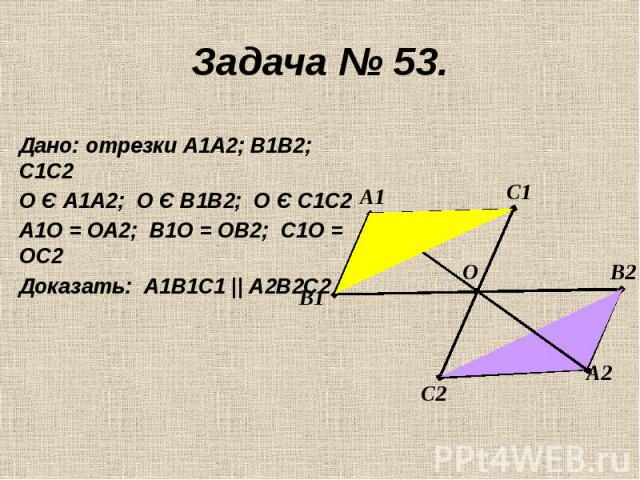
Дано: отрезки А1А2; В1В2; С1С2О Є А1А2; О Є В1В2; О Є С1С2А1О = ОА2; В1О = ОВ2; С1О = ОС2Доказать: А1В1С1 || А2В2С2

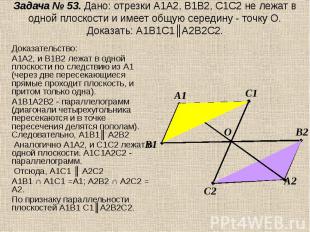
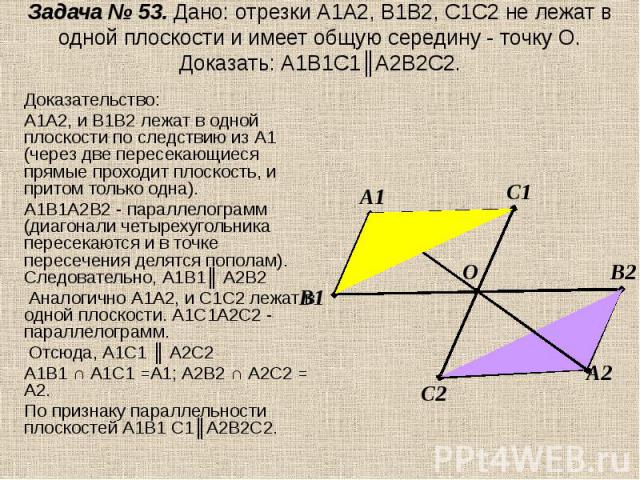
Задача № 53. Дано: отрезки А1А2, В1В2, С1С2 не лежат в одной плоскости и имеет общую середину - точку О. Доказать: А1В1С1║А2В2С2. Доказательство:А1А2, и В1В2 лежат в одной плоскости по следствию из А1 (через две пересекающиеся прямые проходит плоскость, и притом только одна). А1В1А2В2 - параллелограмм (диагонали четырехугольника пересекаются и в точке пересечения делятся пополам). Следовательно, А1В1║ А2В2 Аналогично А1А2, и С1С2 лежат в одной плоскости. А1С1А2С2 - параллелограмм. Отсюда, А1С1 ║ А2С2А1В1 ∩ А1С1 =А1; А2В2 ∩ А2С2 = А2.По признаку параллельности плоскостей А1В1 С1║А2В2С2.

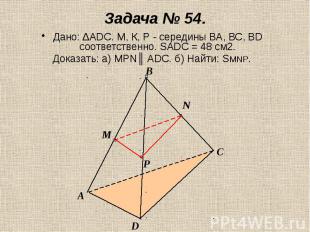
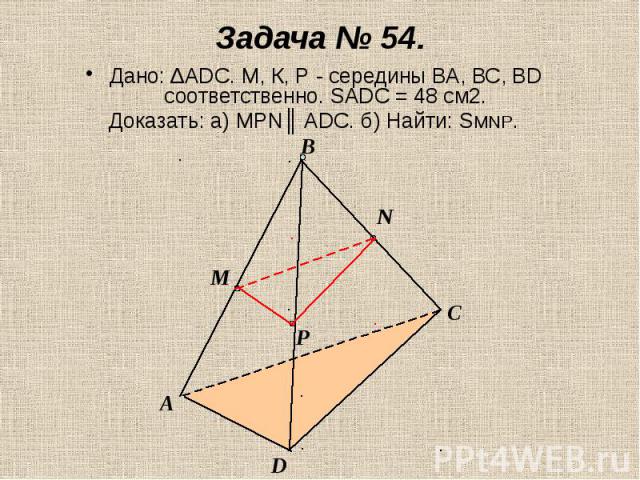
Дано: ΔАDС. М, К, Р - середины ВА, ВС, ВD соответственно. SADC = 48 см2.Доказать: а) МРN║ АDС. б) Найти: SMNP.

Могут ли прямая и плоскость не иметь общих точек?Верно ли, что если две прямые не пересекаются, то они параллельны?Плоскости и β параллельны, прямая m не лежит в плоскости . Верно ли, что прямая m параллельна плоскости β?Верно ли, что если прямая а параллельна одной из двух параллельных плоскостей, с другой плоскостью прямая а имеет одну общую точку?Боковые стороны трапеции параллельны плоскости . Верно ли, что плоскость трапеции параллельна плоскости ?Две стороны трапеции лежат в параллельных плоскостях. Могут ли эти стороны быть боковыми сторонами трапеции?Верно ли, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости?Верно ли, что линия пересечения двух плоскостей параллельна одной из этих плоскостей?Верно ли, что любые четыре точки лежат в одной плоскости?Верно ли, что если две стороны треугольника параллельны плоскости , то и третья сторона параллельна плоскости ?

Могут ли прямая и плоскость не иметь общих точек? ДаВерно ли, что если две прямые не пересекаются, то они параллельны? НетПлоскости и β параллельны, прямая m не лежит в плоскости . Верно ли, что прямая m параллельна плоскости β? ДаВерно ли, что если прямая а параллельна одной из двух параллельных плоскостей, с другой плоскостью прямая а имеет одну общую точку? НетБоковые стороны трапеции параллельны плоскости . Верно ли, что плоскость трапеции параллельна плоскости ? ДаДве стороны трапеции лежат в параллельных плоскостях. Могут ли эти стороны быть боковыми сторонами трапеции? НетВерно ли, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости? НетВерно ли, что линия пересечения двух плоскостей параллельна одной из этих плоскостей? НетВерно ли, что любые четыре точки лежат в одной плоскости? НетВерно ли, что если две стороны треугольника параллельны плоскости , то и третья сторона параллельна плоскости ? Да

П. 10, № 55, 56, 57.Пояснения к домашнему заданию:В № 55 запишите в тетрадь и разберите решение задачи, приведенное в учебнике.Дополнительная задача: Прямая а параллельна плоскости . Существует ли плоскость, проходящая через прямую а и параллельная плоскости . Если существует, то сколько таких плоскостей? Ответ обоснуйте.