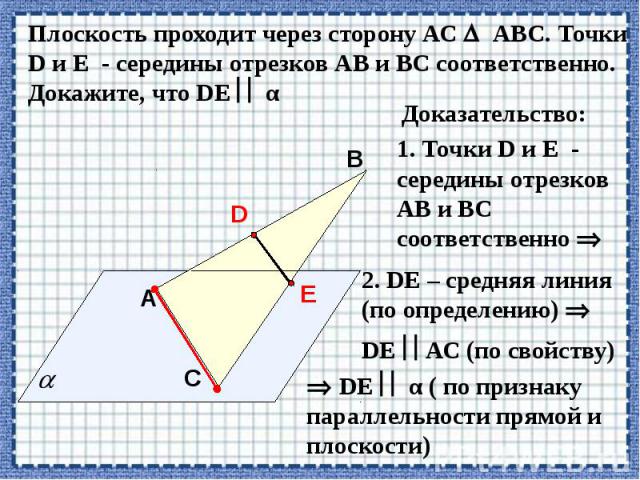
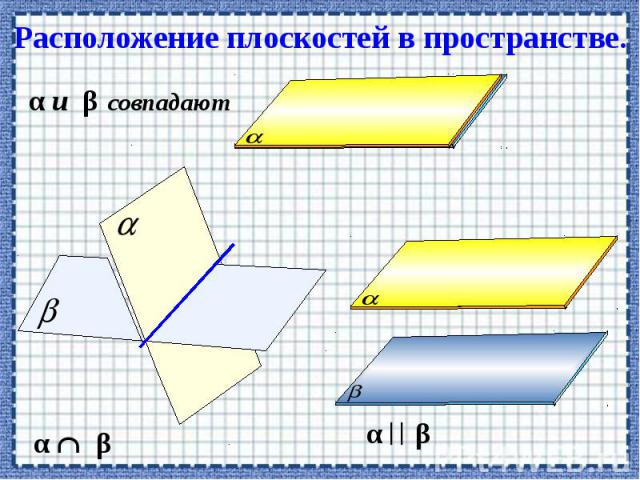
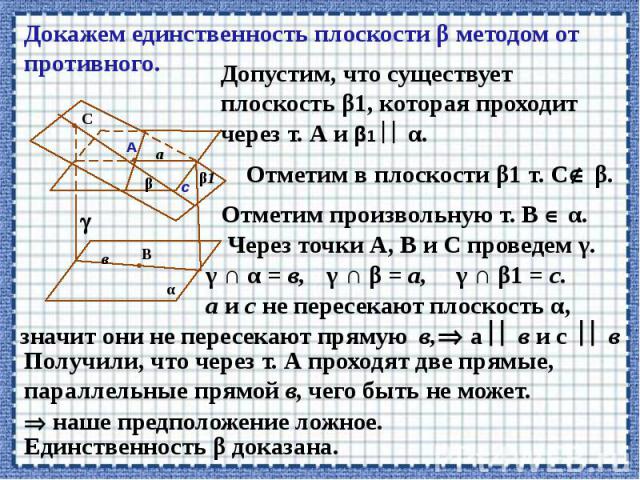
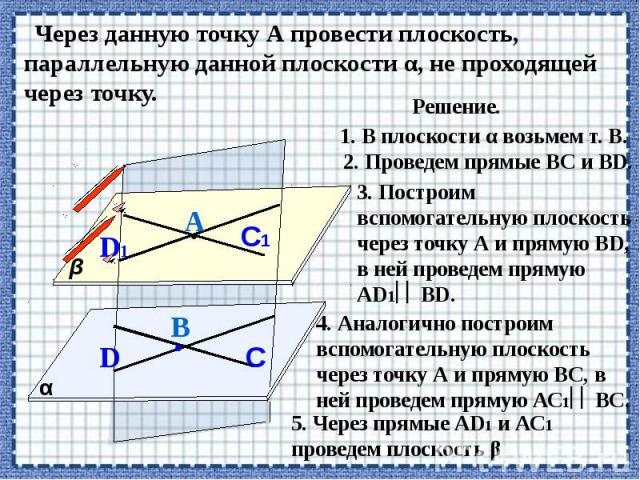
Презентация на тему: Параллельность прямых и плоскостей в пространстве

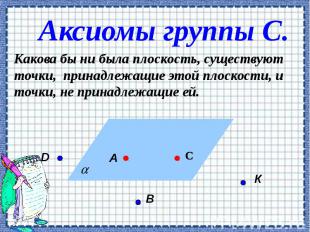
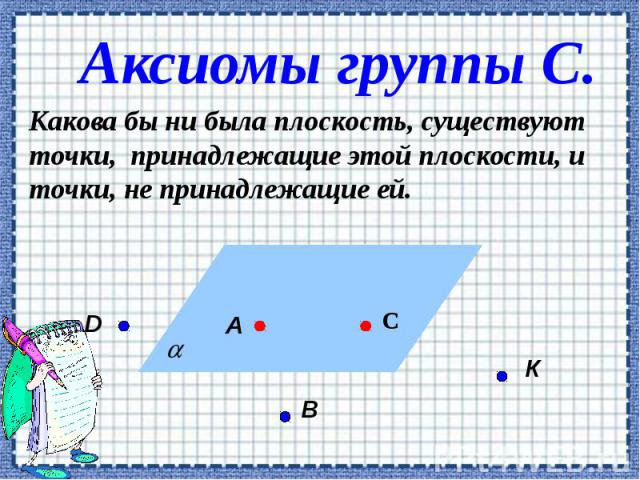
Аксиомы группы С. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

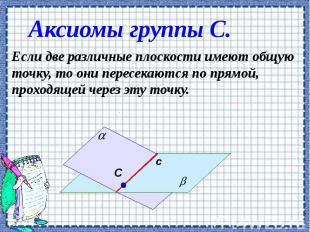
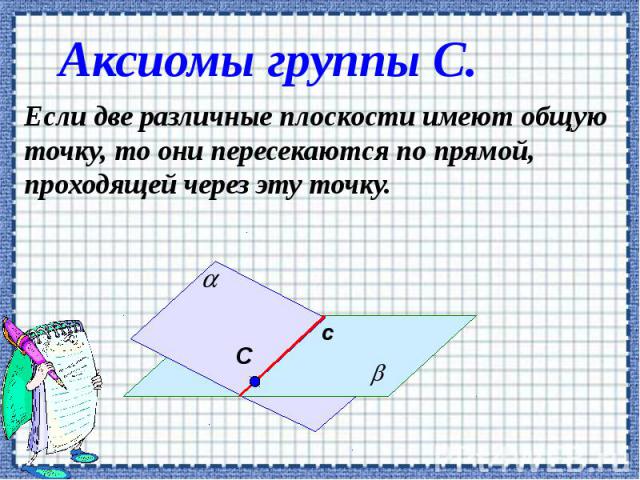
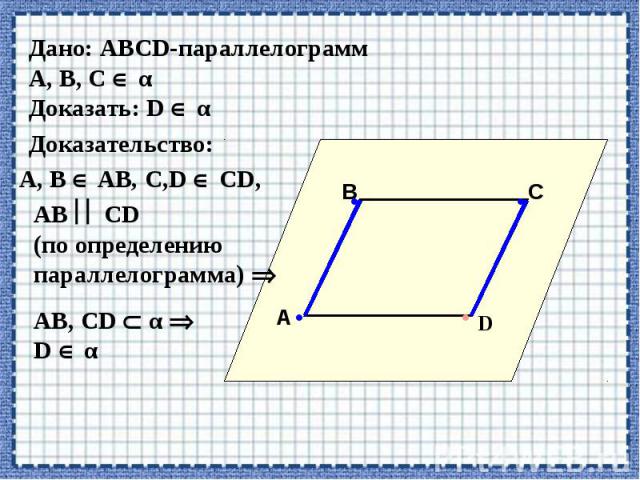
Аксиомы группы С. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

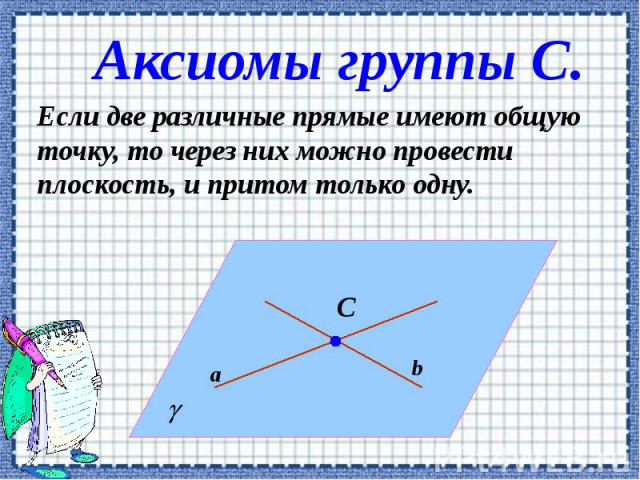
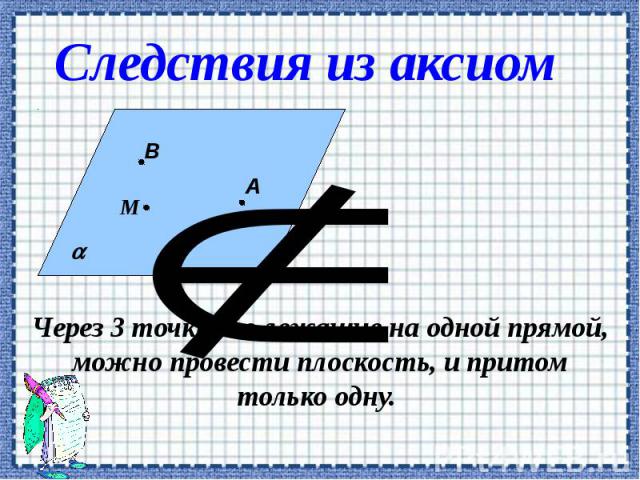
Аксиомы группы С. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

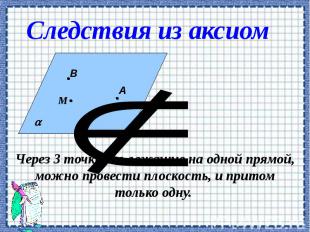
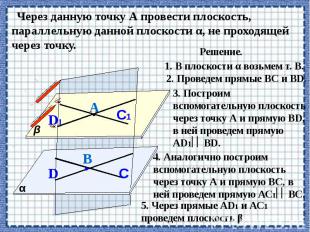
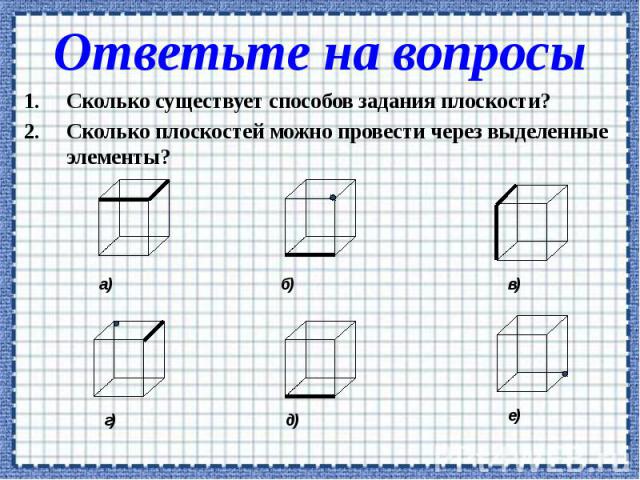
Сколько существует способов задания плоскости? Сколько существует способов задания плоскости? Сколько плоскостей можно провести через выделенные элементы?

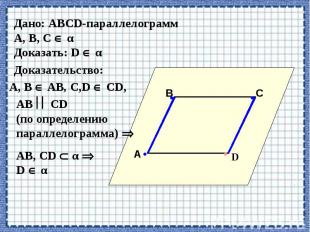
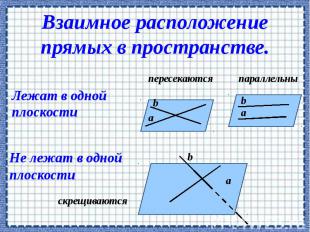
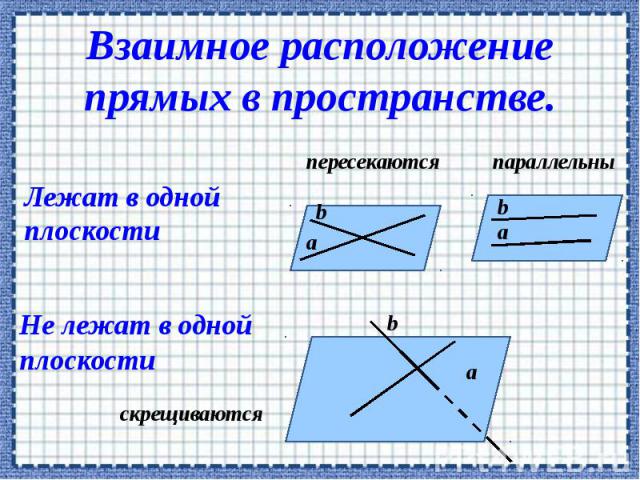
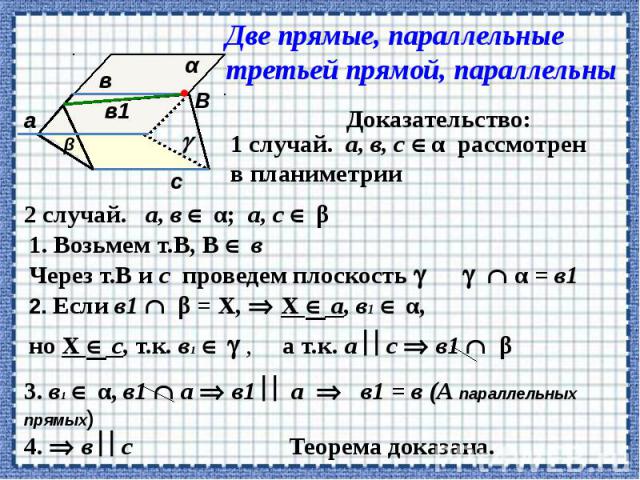
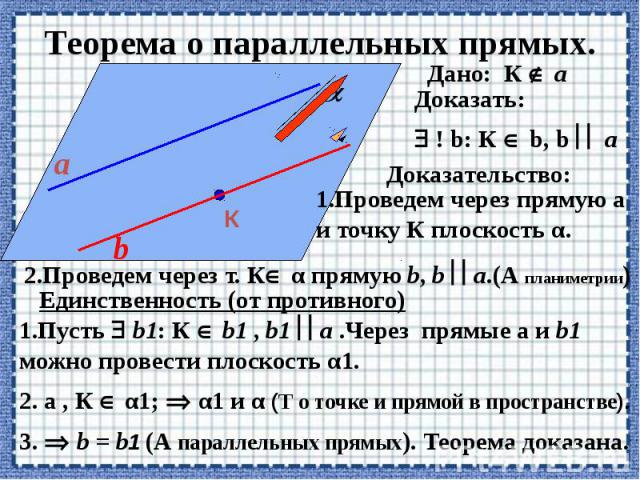
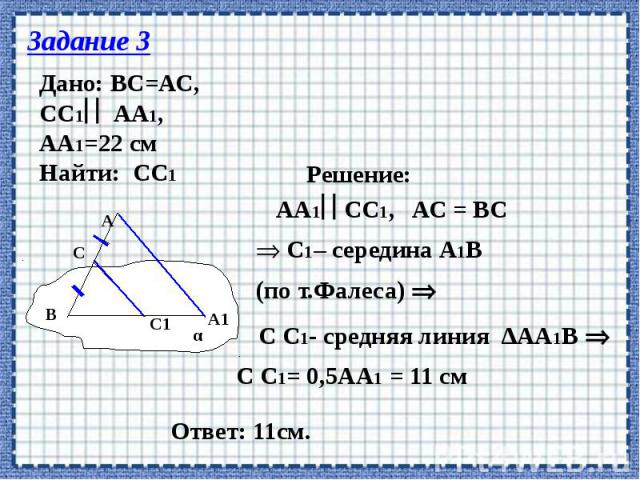
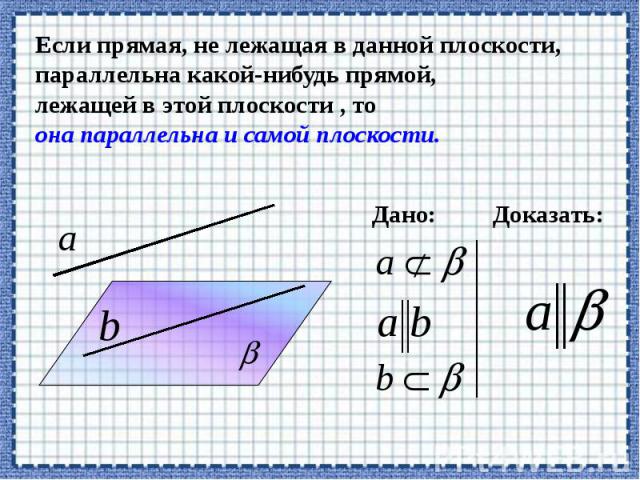
Теорема о параллельных прямых.

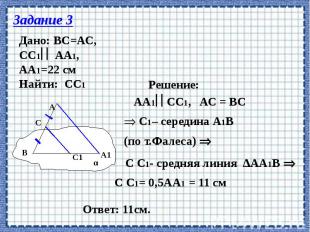
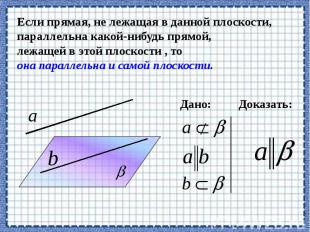
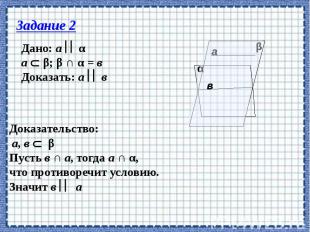
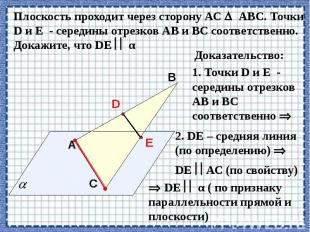
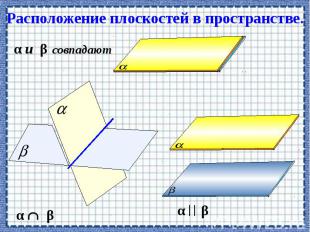
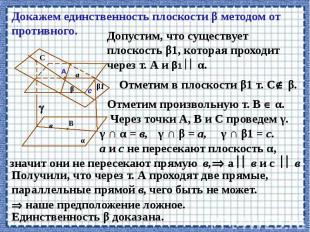
Определите: верно, ли утверждение? 1. если плоскости не пересекаются, то они параллельны. 2. плоскости параллельны, если прямая лежащая в одной плоскости, параллельна другой плоскости? 3. если две прямые, лежащие в одной плоскости, параллельны двум прямым другой плоскости, то эти плоскости параллельны? 4. если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой плоскости. 5. прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны. 6. Если прямая пересекает одну из двух плоскостей, то она пересекает и другую. 7. Две плоскости, параллельные третьей, параллельны. 8. Отрезки прямых, заключенные между параллельными плоскостями, равны.