Презентация на тему: параллельность прямых и плоскостей 10 класс

ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

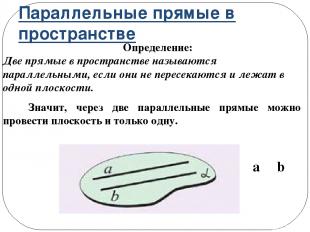
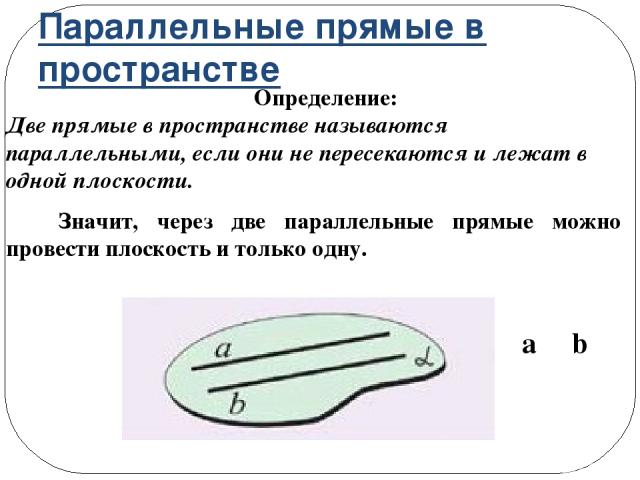
Параллельные прямые в пространстве Определение: Две прямые в пространстве называются параллельными, если они не пересекаются и лежат в одной плоскости. Значит, через две параллельные прямые можно провести плоскость и только одну. a ΙΙ b

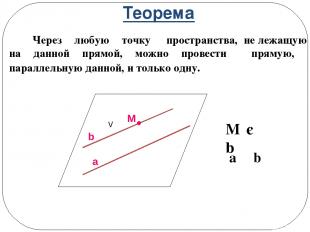
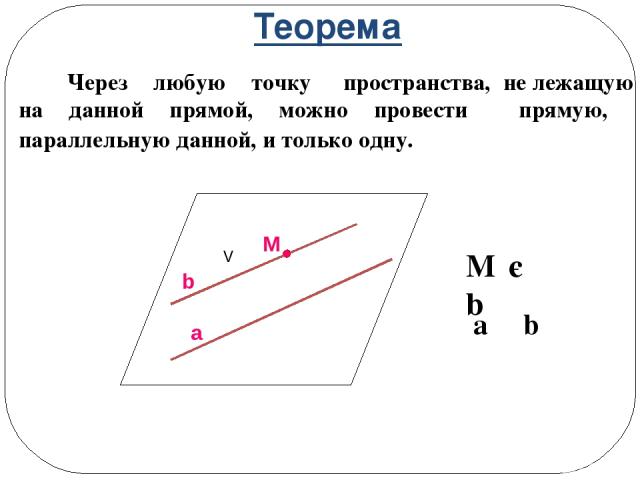
Теорема Через любую точку пространства, не лежащую на данной прямой, можно провести прямую, параллельную данной, и только одну. M є b a ΙΙ b a V M b

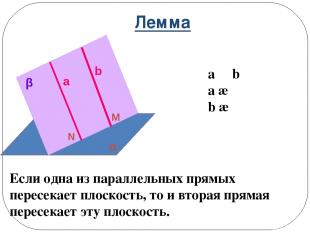
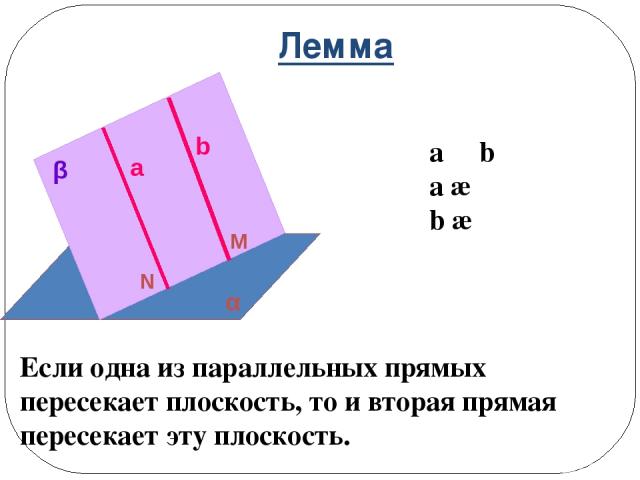
Лемма a ΙΙ b a ∩ α b ∩ α Если одна из параллельных прямых пересекает плоскость, то и вторая прямая пересекает эту плоскость. a b α β M N

ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ Если две прямые параллельны третьей прямой, то они параллельны между собой. a ΙΙ b a ΙΙ c b ΙΙ c

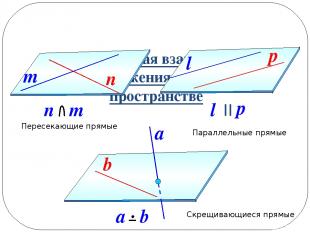
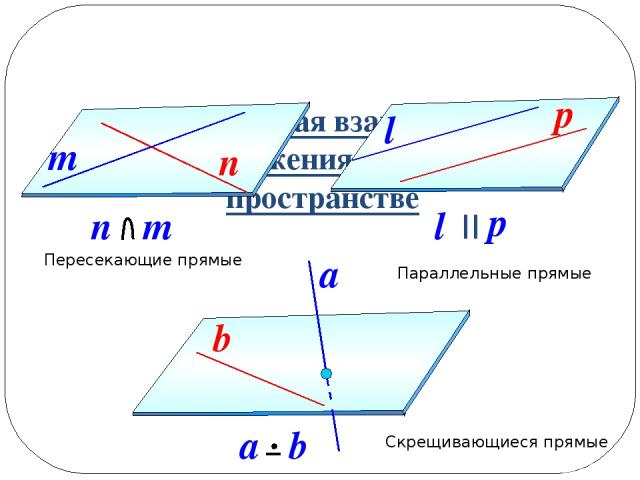
Три случая взаимного расположения прямых в пространстве Пересекающие прямые Параллельные прямые Скрещивающиеся прямые n m n m p l l p II a a b

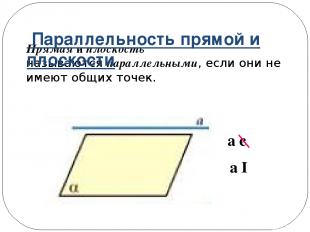
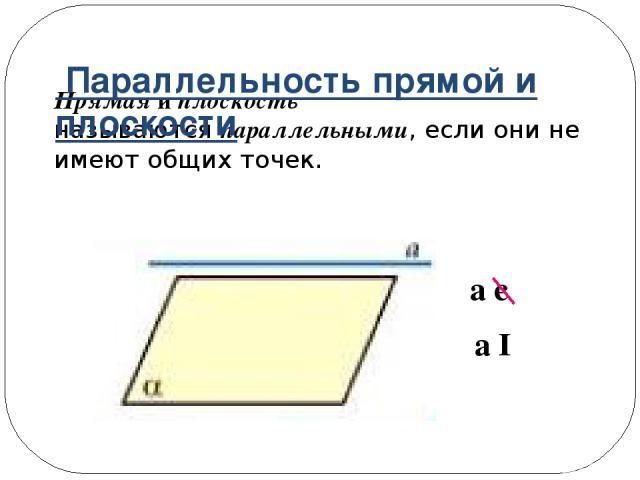
Прямая и плоскость называются параллельными, если они не имеют общих точек. a є α a ǁ α Параллельность прямой и плоскости

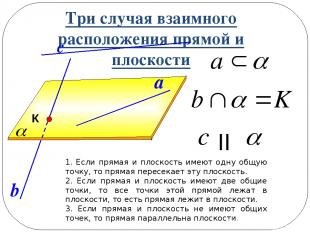
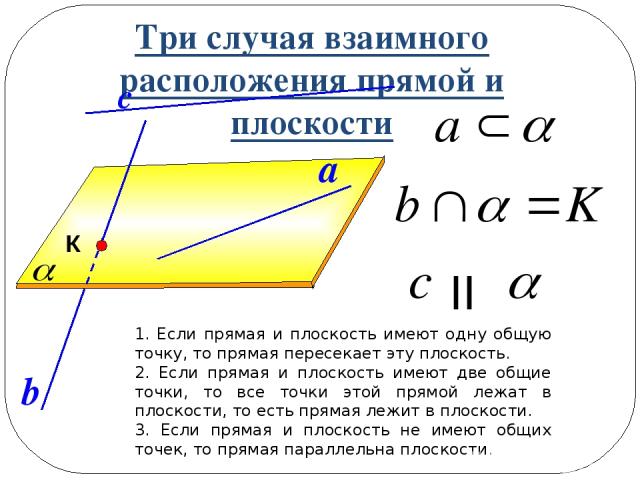
Три случая взаимного расположения прямой и плоскости 1. Если прямая и плоскость имеют одну общую точку, то прямая пересекает эту плоскость. 2. Если прямая и плоскость имеют две общие точки, то все точки этой прямой лежат в плоскости, то есть прямая лежит в плоскости. 3. Если прямая и плоскость не имеют общих точек, то прямая параллельна плоскости. b К a с II

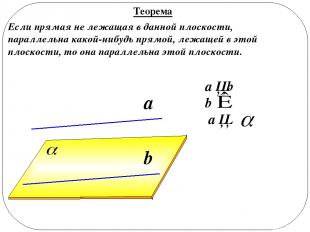
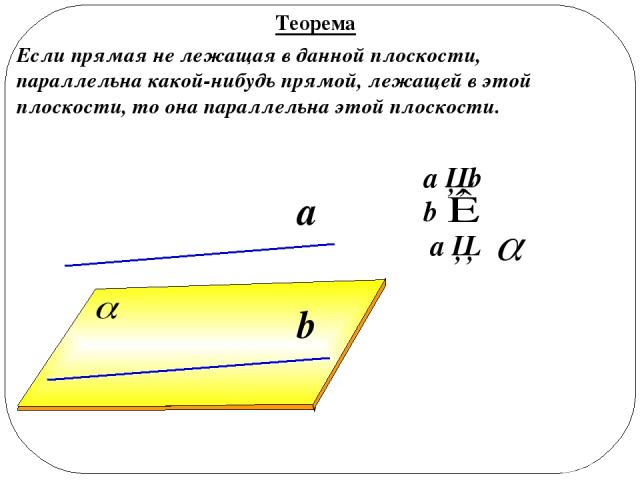
a ││b b a ││ a b Теорема Если прямая не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна этой плоскости.

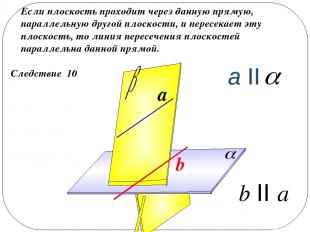
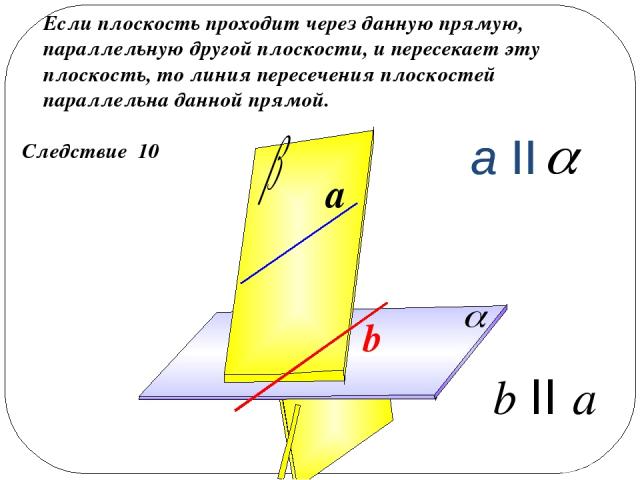
Следствие 10 Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. a b II a b a II a II

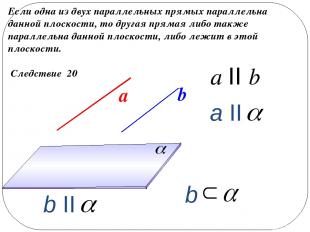
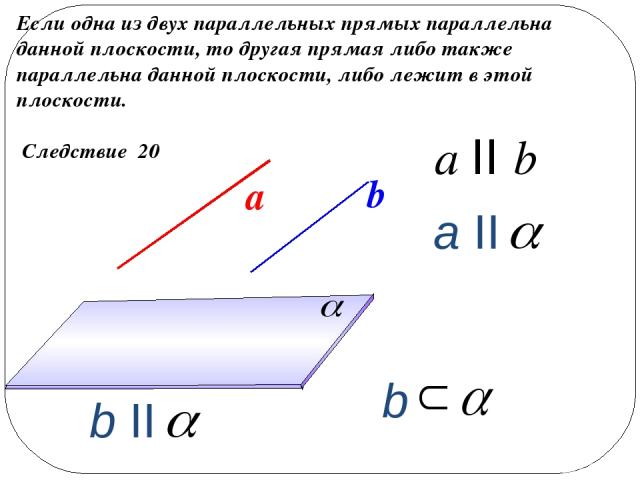
Следствие 20 Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости. a II b а b a II b II b

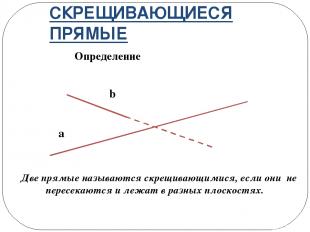
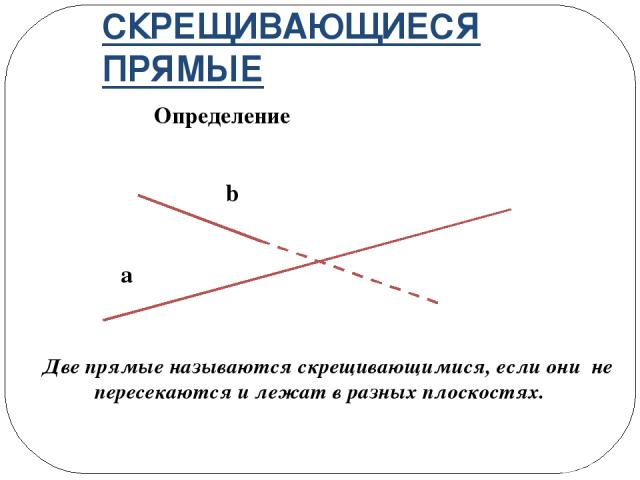
СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ Определение a b Две прямые называются скрещивающимися, если они не пересекаются и лежат в разных плоскостях.

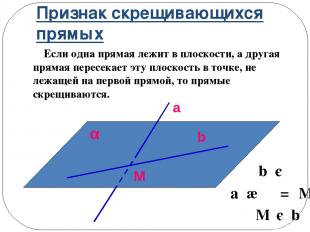
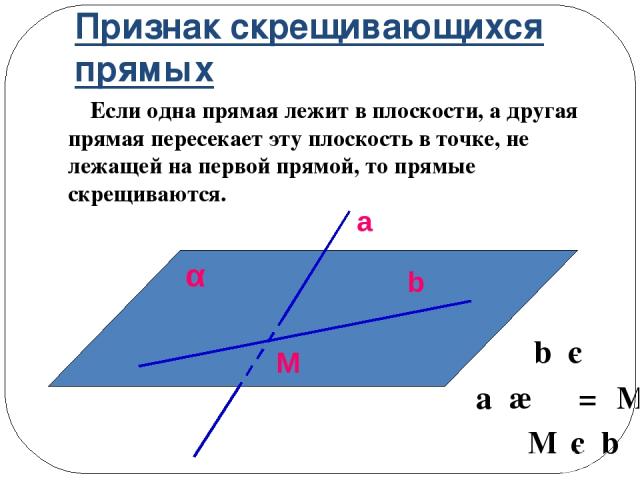
Признак скрещивающихся прямых Если одна прямая лежит в плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то прямые скрещиваются. b є α a ∩ α = M M є b a b α M

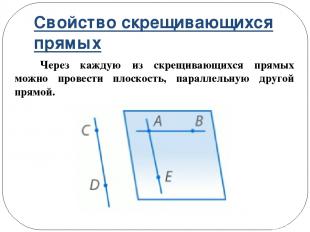
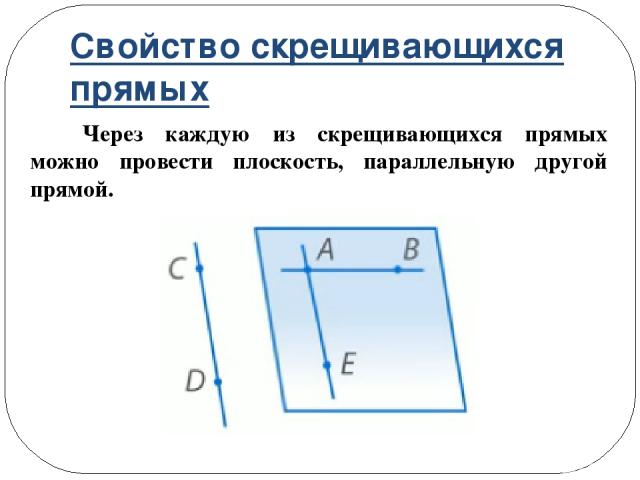
Свойство скрещивающихся прямых Через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.

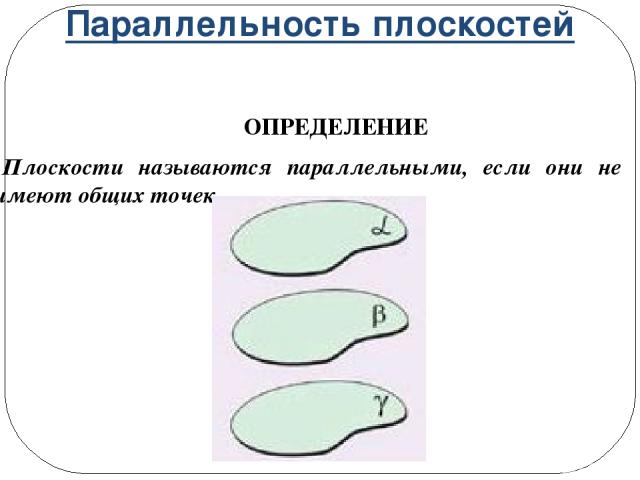
Параллельность плоскостей ОПРЕДЕЛЕНИЕ Плоскости называются параллельными, если они не имеют общих точек.

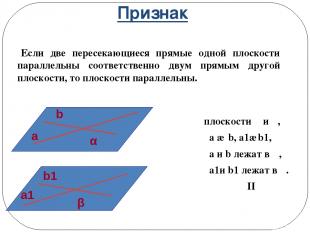
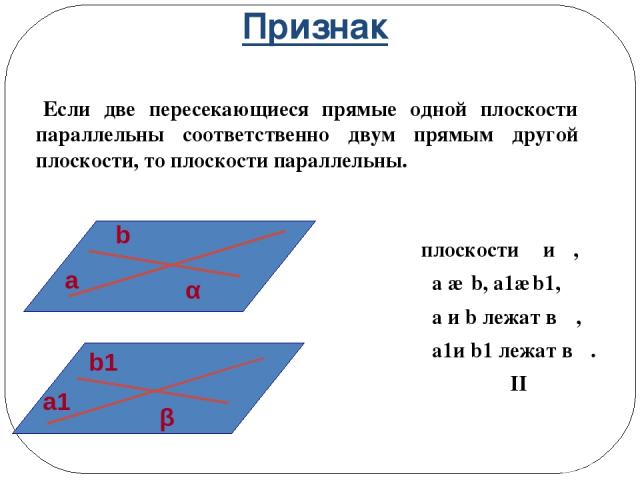
Признак плоскости α и β, a ∩ b, a1∩b1, a и b лежат в α, a1и b1 лежат в β. α II β Если две пересекающиеся прямые одной плоскости параллельны соответственно двум прямым другой плоскости, то плоскости параллельны. a b α b1 a1 β

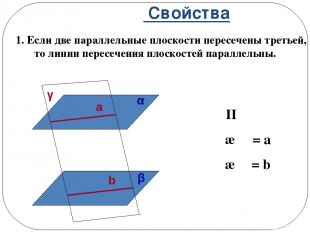
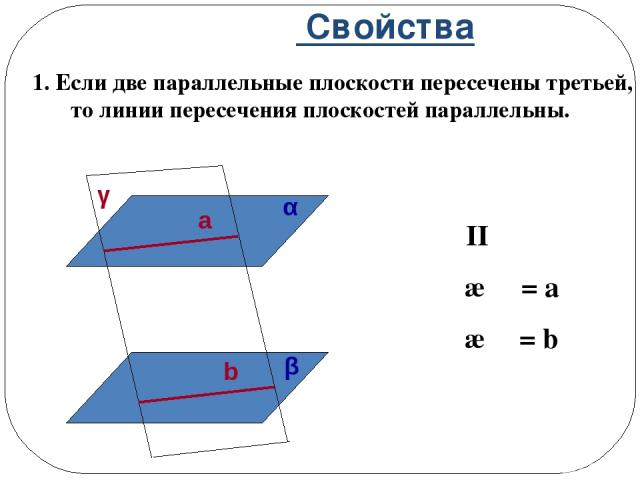
Свойства 1. Если две параллельные плоскости пересечены третьей, то линии пересечения плоскостей параллельны. α II β γ ∩ α = a γ ∩ β = b α β γ a b

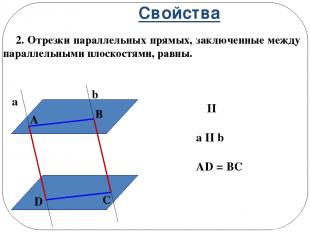
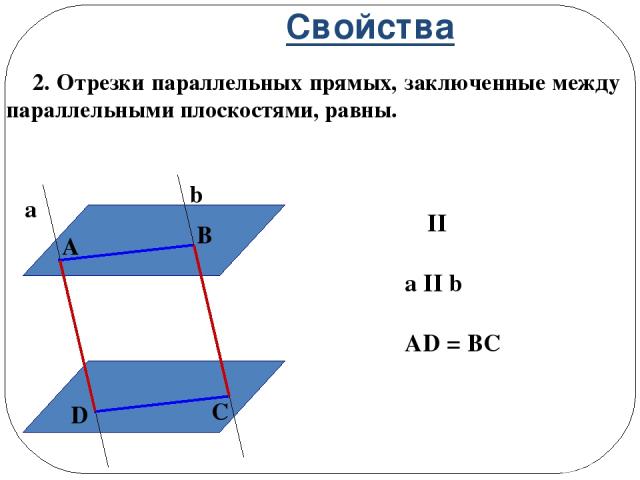
Свойства 2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. α II β a II b AD = BC α β a b А B C D

Спасибо за внимание!