Презентация на тему: Построения в пространстве

Построения в пространстве.геометрия 10

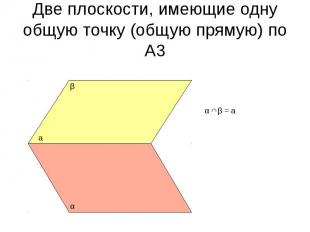
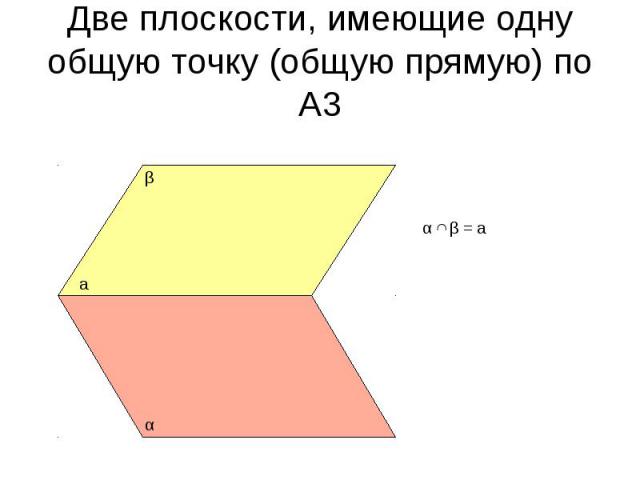
Две плоскости, имеющие одну общую точку (общую прямую) по А3

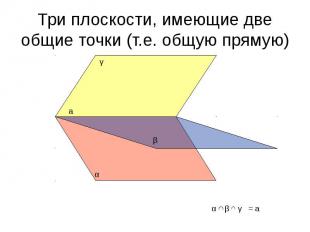
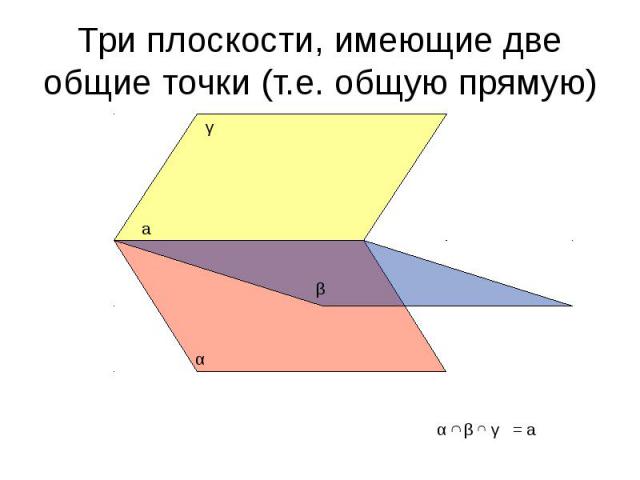
Три плоскости, имеющие две общие точки (т.е. общую прямую)

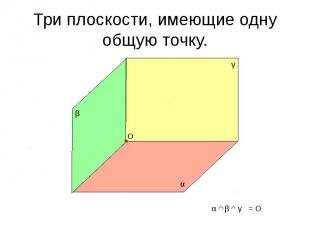
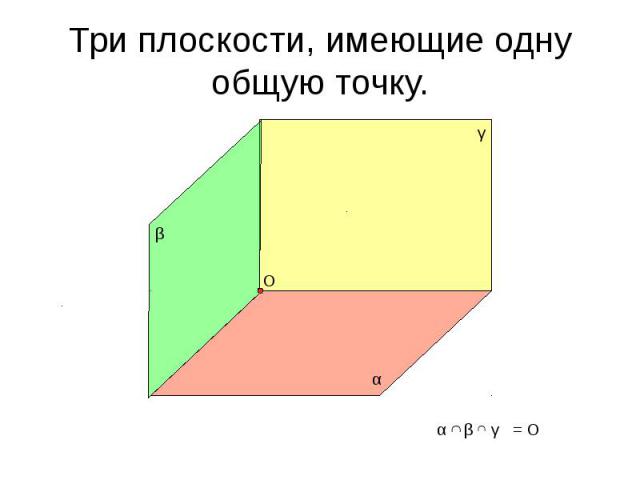
Три плоскости, имеющие одну общую точку.

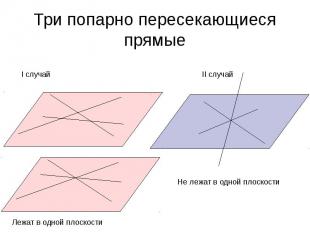
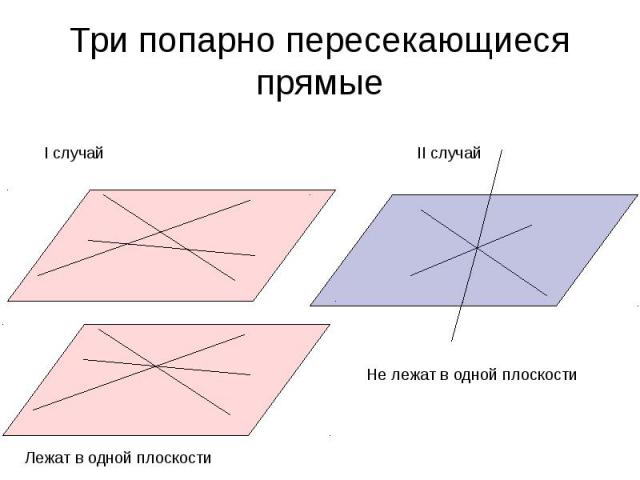
Три попарно пересекающиеся прямые I случай Лежат в одной плоскости Не лежат в одной плоскости

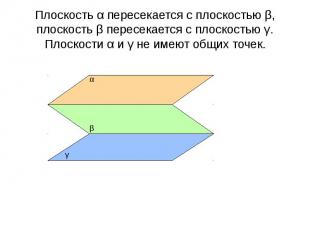
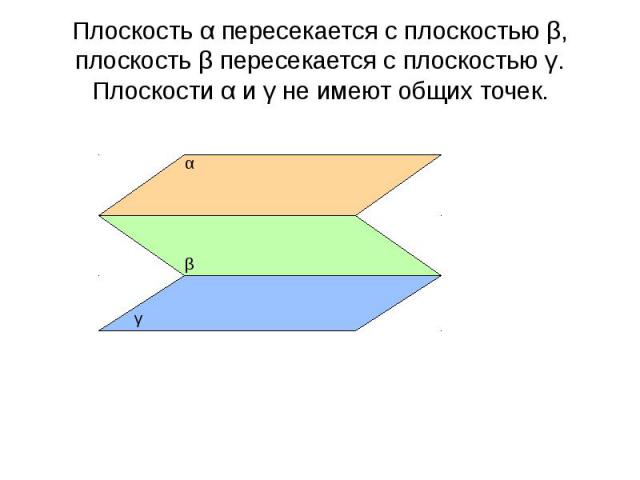
Плоскость α пересекается с плоскостью β, плоскость β пересекается с плоскостью γ. Плоскости α и γ не имеют общих точек.

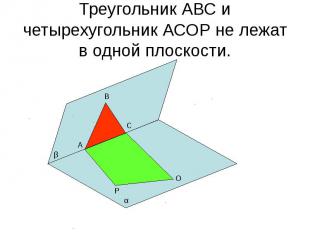
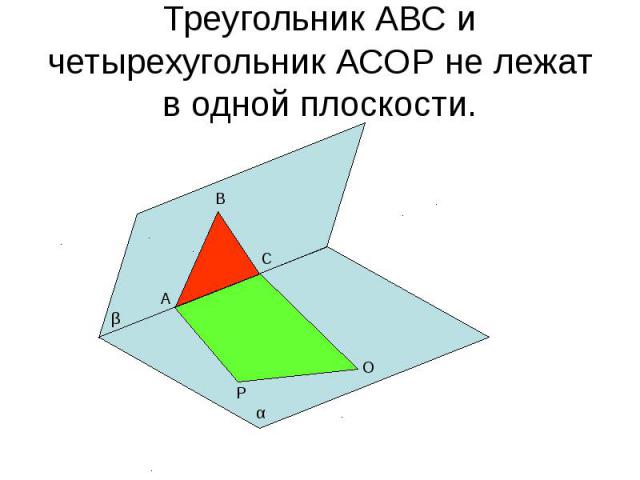
Треугольник АВС и четырехугольник АСОР не лежат в одной плоскости.

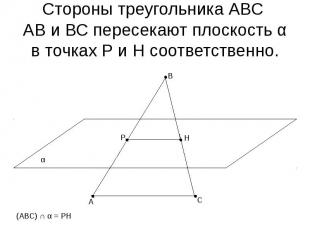
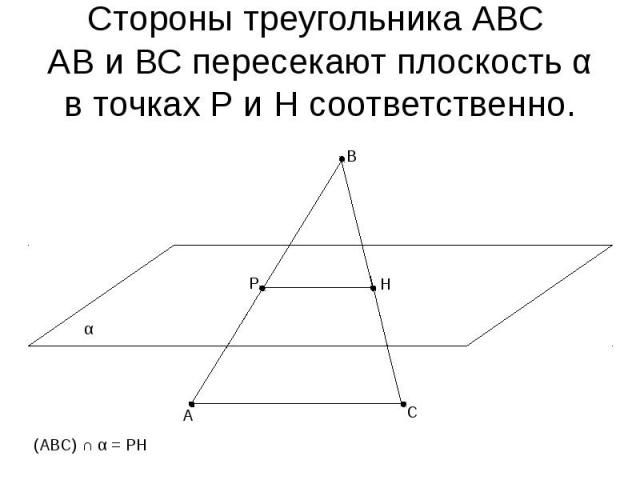
Стороны треугольника АВС АВ и ВС пересекают плоскость α в точках Р и Н соответственно.

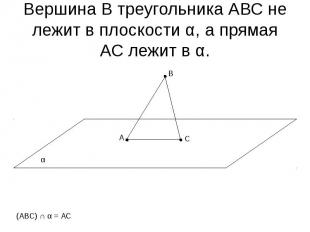
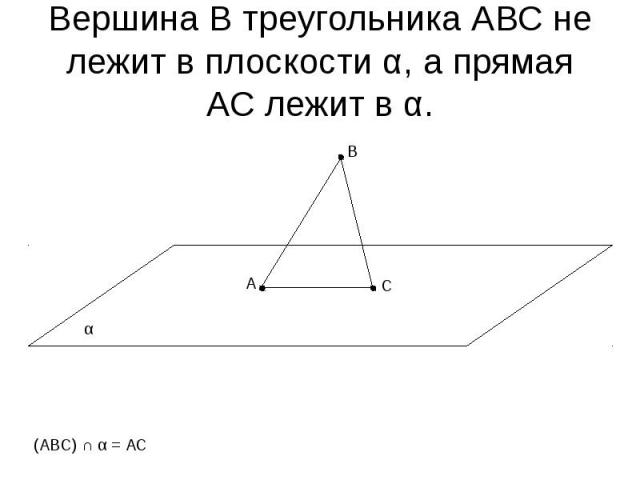
Вершина В треугольника АВС не лежит в плоскости α, а прямая АС лежит в α.

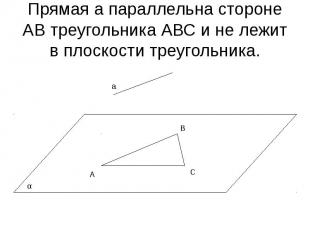
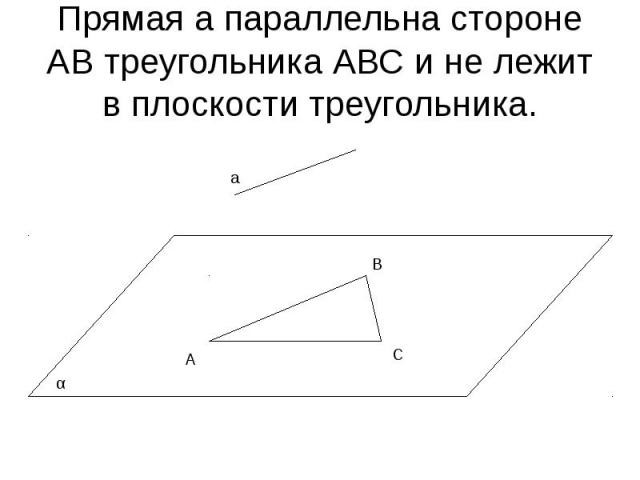
Прямая а параллельна стороне АВ треугольника АВС и не лежит в плоскости треугольника.

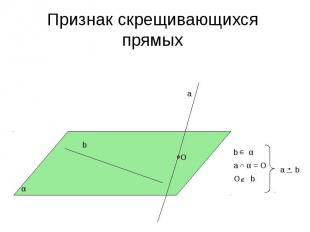
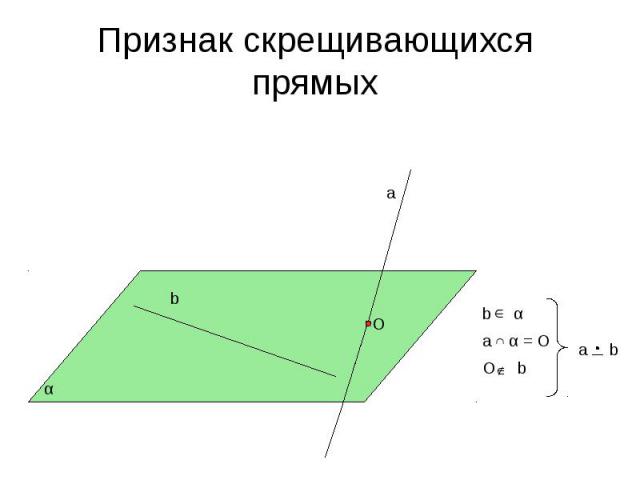
Признак скрещивающихся прямых

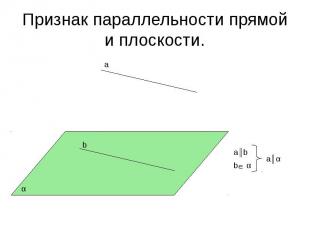
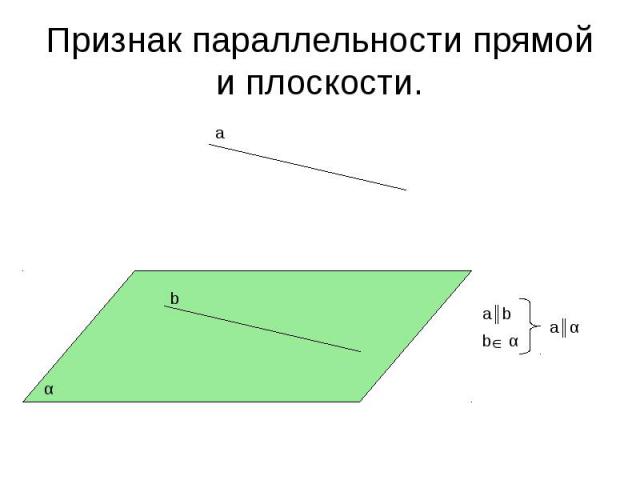
Признак параллельности прямой и плоскости.

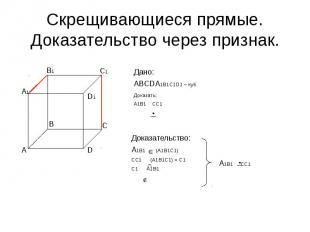
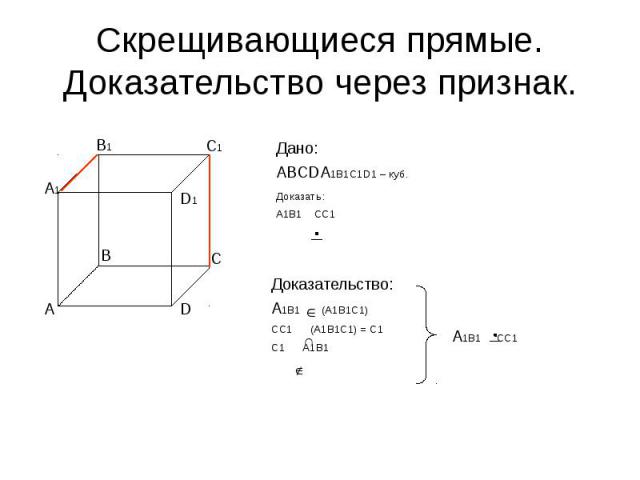
Скрещивающиеся прямые. Доказательство через признак. Дано:АВСDA1B1C1D1 – куб.Доказать:А1В1 СС1 Доказательство:А1В1 (А1В1С1)СС1 (А1В1С1) = С1С1 А1В1

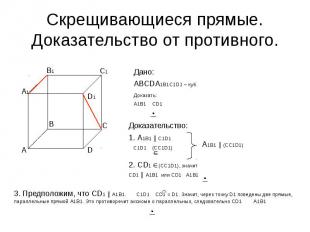
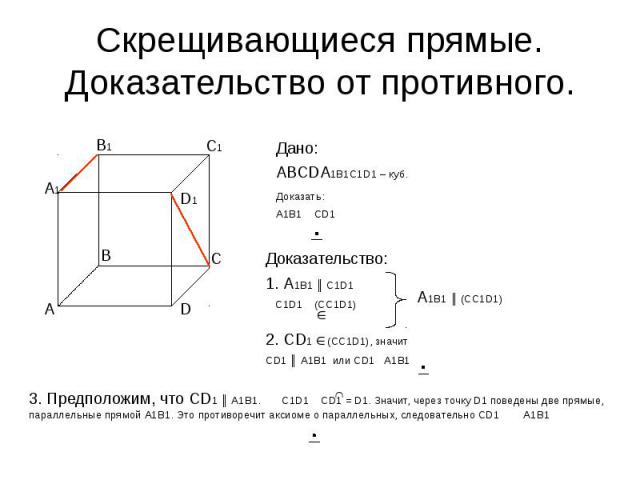
Скрещивающиеся прямые. Доказательство от противного. Дано:АВСDA1B1C1D1 – куб.Доказать:А1В1 СD1 Доказательство:1. А1В1 ║ С1D1 С1D1 (CC1D1) 2. СD1 (CC1D1), значит СD1 ║ А1В1 или СD1 А1В1 3. Предположим, что СD1 ║ А1В1. C1D1 CD1 = D1. Значит, через точку D1 поведены две прямые, параллельные прямой А1В1. Это противоречит аксиоме о параллельных, следовательно СD1 А1В1