Презентация на тему: Перпендикулярность прямой и плоскости

Перпендикулярность прямой и плоскости

Перпендикулярные прямые в пространствеДве прямые в пространстве называются перпендикулярными (взаимно перпендикулярными) , если угол между ними равен 90°. Перпендикулярность прямых a и b обозначается так: a b. Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися. На рисунке 1 перпендикулярные прямые a и b пересекаются, а перпендикулярные прямые a и c скрещивающиеся.

Докажем лемму о перпендикулярности двух параллельных прямых к третьей прямой Лемма:Если одна из двух параллельных прямых перпендикулярна к третьей прямой , то и другая прямая перпендикулярна к этой прямой.Доказательство: Пусть a || b и a b. Докажем, что b c. Через произвольную т. М пространства, не лежащую на данных прямых, проведем прямые МА и МС, параллельные соответственно прямым a и c. Так как a c, то AMC = 90°. По условию b || а, а по построению а || МА, поэтому b || МА. Итак, прямые b и с параллельны соответственно прямым МА и МС, угол между которыми равен 90°. Это означает, что угол между прямыми b и с также равен 90°, т. е. b c.

Параллельные прямые, перпендикулярные к плоскостиПрямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.Перпендикулярность прямой а и плоскости α обозначается так: а α. Если прямая а перпендикулярна к плоскости α, то она пересекает эту плоскость. В самом деле, если бы прямая а не пересекала плоскость α, то она или лежала бы в этой плоскости, или была бы параллельна ей. Но тогда в плоскости α имелись бы прямые, не перпендикулярные к прямой а, например прямые, параллельные ей, что противоречит определению перпендикулярности прямой и плоскости. Значит, прямая а пересекает плоскость α.

На рисунке 3 изображена прямая а, перпендикулярная к плоскости α.Окружающая нас обстановка дает много примеров, иллюстрирующих перпендикулярность прямой и плоскости. Непокосившийся телеграфный столб стоит прямо, т. е. перпендикулярно к плоскости земли. Так же расположены колонны здания по отношению к плоскости фундамента, линии пересечения стен по отношению к плоскости пола и т. д.

Докажем две теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярностью к плоскостиЕсли одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости. Доказательство: Рассмотрим две параллельные прямые а и b и плоскость α, такую, что аα. Докажем, что и b α. Проведем какую-нибудь прямую х в плоскости α (рисунок 4). Так как а α, то а х. По лемме о перпендикулярности двух параллельных прямых к третьей b х. Таким образом, прямая b перпендикулярна к любой прямой, лежащей в плоскости α, т.е. b α.

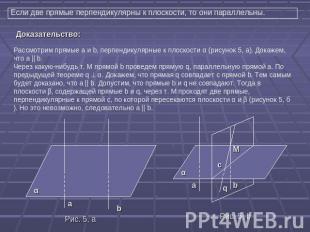
Если две прямые перпендикулярны к плоскости, то они параллельны. Доказательство: Рассмотрим прямые а и b, перпендикулярные к плоскости α (рисунок 5, a). Докажем, что а || b.Через какую-нибудь т. M прямой b проведем прямую q, параллельную прямой а. По предыдущей теореме q α. Докажем, что прямая q совпадает с прямой b. Тем самым будет доказано, что а || b. Допустим, что прямые b и q не совпадают. Тогда в плоскости β, содержащей прямые b и q, через т. M проходят две прямые, перпендикулярные к прямой c, по которой пересекаются плоскости α и β (рисунок 5, б). Но это невозможно, следовательно а || b.