Презентация на тему: Подобие треугольников. Первый признак подобия

Подобие треугольников.Первый признак подобия

Изобразим: а) две неравные окружности; б) два неравных квадрата; в) два неравных равнобедренных прямоугольных треугольника; г) два неравных равносторонних треугольника.Чем отличаются фигуры в каждой представленной паре? Что у них общего? Почему они не равны?

Определение. Два треугольника называются подобными, если углы одного соответственно равны углам другого и соответствующие стороны пропорциональны. Коэффициент пропорциональности называется коэффициентом подобия.

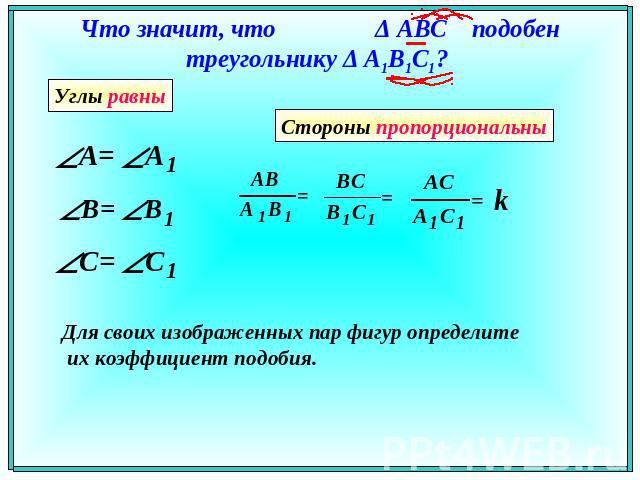
Что значит, что Δ АВС подобен треугольнику Δ A1В1С1? Для своих изображенных пар фигур определите их коэффициент подобия.
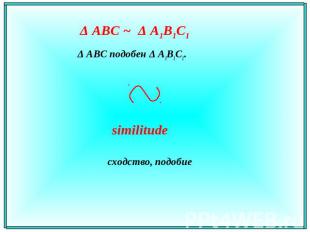
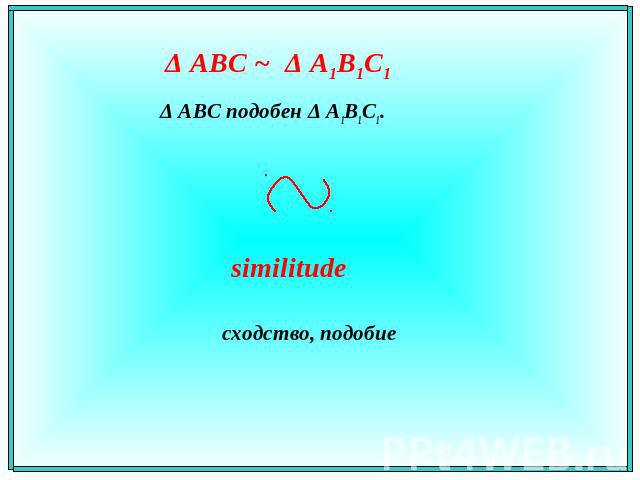
Δ АВС ~ Δ A1В1С1 Δ АВС подобен Δ A1В1С1. similitudeсходство, подобие

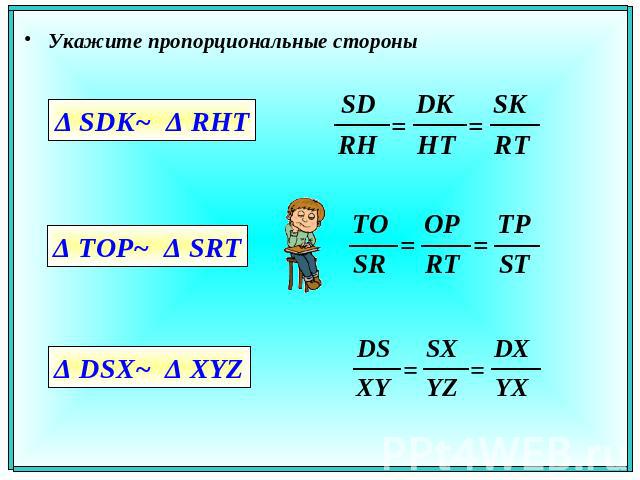
Укажите пропорциональные стороны
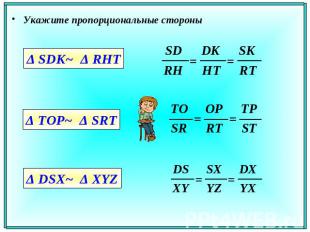
Укажите пропорциональные стороны

Стороны треугольника равны 5 см, 8 см и 10 см. Найдите стороны подобного ему треугольника, если коэффициент подобия равен: а) 0,5; б) 2.
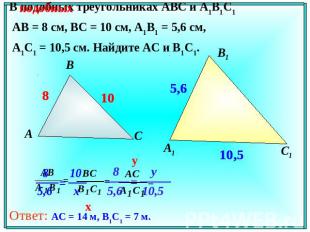
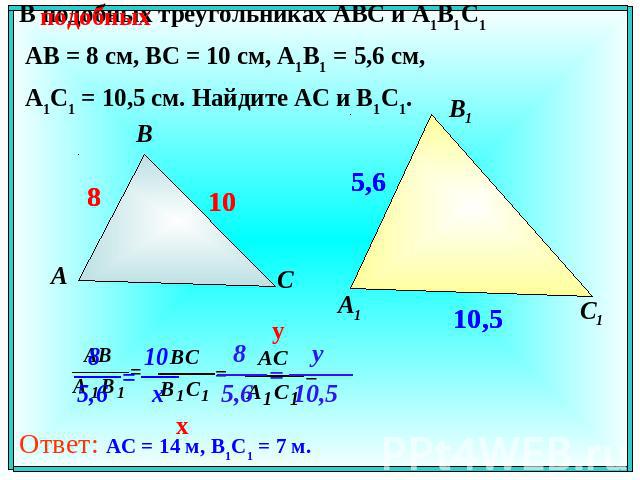
В подобных треугольниках АВС и А1В1С1 АВ = 8 см, ВС = 10 см, А1В1 = 5,6 см, А1С1 = 10,5 см. Найдите АС и В1С1.

– Пройдите глазами по знаку подобия.– Закройте глаза. – Расслабьте мышцы лба.– Медленно переведите глазные яблоки в крайнее левое положение.– Почувствуйте напряжение глазных мышц.– Зафиксируйте положение– Теперь медленно с напряжением переведите глаза вправо.– Повторите четыре раза.– Откройте глаза.– Пройдите глазами по знаку подобия.
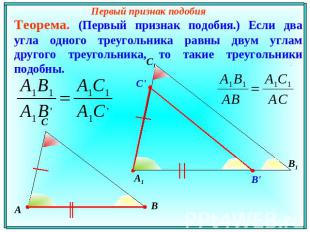
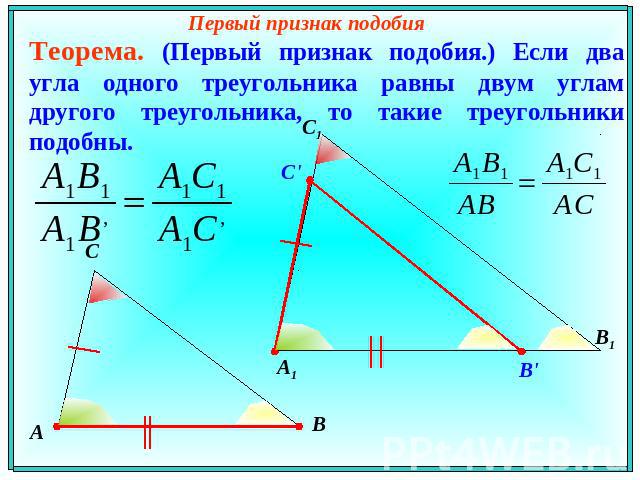
Первый признак подобия Теорема. (Первый признак подобия.) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Теорема. (Первый признак подобия треугольников.) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
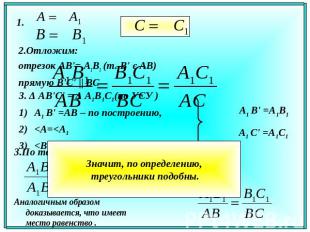
Значит, по определению, треугольники подобны. Аналогичным образом доказывается, что имеет место равенство .

Подобны ли прямоугольные треугольники, если у одного из них есть угол 40о, а у другого 50о?Два треугольника подобны. Два угла одного треугольника равны 55о и 80о. Найдите наименьший угол второго треугольника.
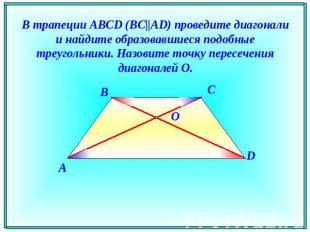
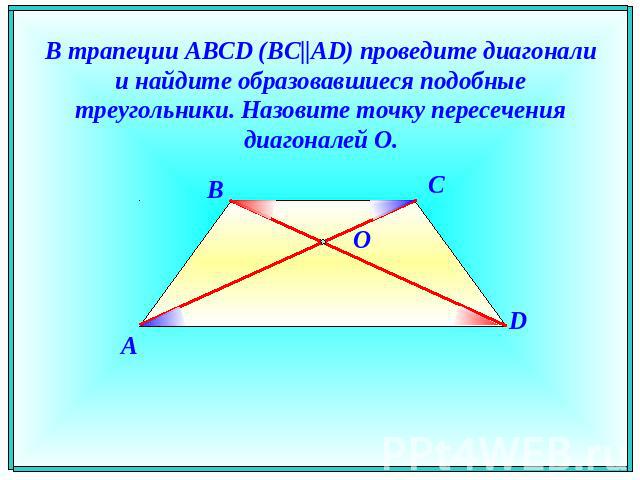
В трапеции ABCD (BC||AD) проведите диагонали и найдите образовавшиеся подобные треугольники. Назовите точку пересечения диагоналей O.