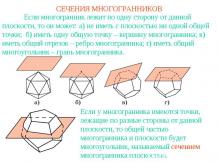
Презентация на тему: Двугранный угол

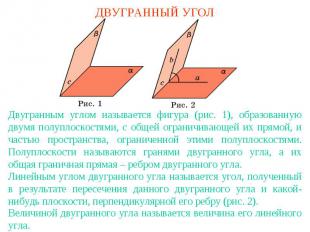
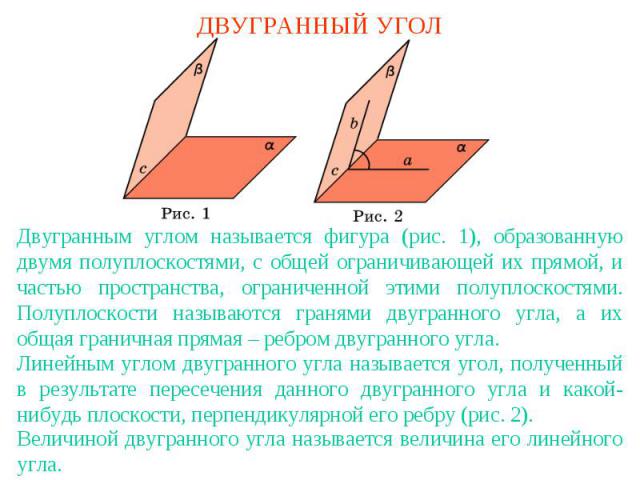
ДВУГРАННЫЙ УГОЛДвугранным углом называется фигура (рис. 1), образованную двумя полуплоскостями, с общей ограничивающей их прямой, и частью пространства, ограниченной этими полуплоскостями. Полуплоскости называются гранями двугранного угла, а их общая граничная прямая – ребром двугранного угла. Линейным углом двугранного угла называется угол, полученный в результате пересечения данного двугранного угла и какой-нибудь плоскости, перпендикулярной его ребру (рис. 2).Величиной двугранного угла называется величина его линейного угла.

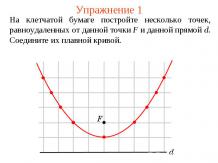
Упражнение 1Какой угол образует ребро двугранного угла с любой прямой, лежащей в плоскости его линейного угла?

Упражнение 2Плоскости двух равнобедренных треугольников с общим основанием образуют двугранный угол. Верно ли утверждение о том, что высоты, проведенные к общему основанию треугольников, образуют линейный угол двугранного угла?

Упражнение 3Треугольник MAB и квадрат ABCD заданы таким образом, что MB - перпендикуляр к плоскости квадрата. Какой угол можно считать углом между плоскостями AMD и ABC?

Упражнение 4В правильной треугольной призме найдите угол между боковыми гранями.

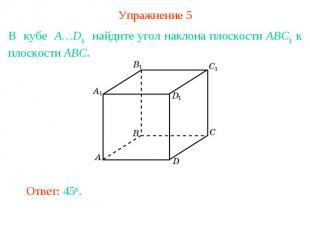
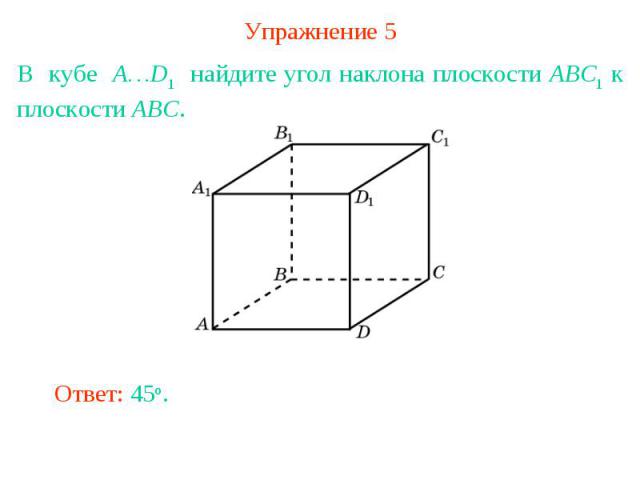
Упражнение 5В кубе A…D1 найдите угол наклона плоскости ABC1 к плоскости ABC.

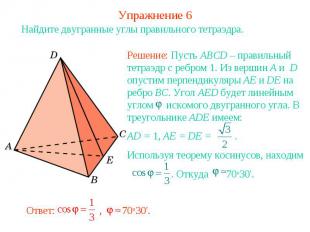
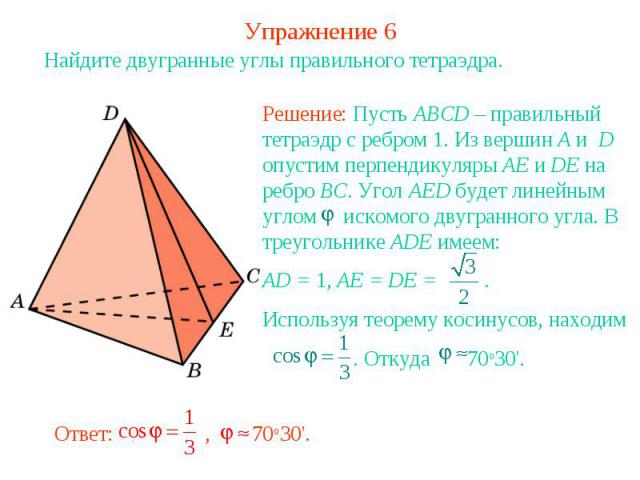
Упражнение 6Найдите двугранные углы правильного тетраэдра.Решение: Пусть ABCD – правильный тетраэдр с ребром 1. Из вершин A и D опустим перпендикуляры AE и DE на ребро BC. Угол AED будет линейным углом искомого двугранного угла. В треугольнике ADE имеем:AD = 1, AE = DE = . Используя теорему косинусов, находим . Откуда 70о30'.

Упражнение 7Найдите геометрическое место точек в пространстве, равноудаленных от двух пересекающихся плоскостей. Ответ: Две биссектральные плоскости.

Упражнение 8Через сторону BC треугольника ABC проведена плоскость под углом 30° к плоскости треугольника. Высота AD треугольника ABC равна a. Найдите расстояние от вершины A треугольника до плоскости α.

Упражнение 9Через катет BC=a равнобедренного прямоугольного треугольника ABC (угол C равен 90°) проведена плоскость α, образующая с плоскостью треугольника угол 30°. Найдите расстояние от вершины A до плоскости α.

Упражнение 10Через сторону BC треугольника ABC проведена плоскость под углом 30° к плоскости треугольника; угол C равен 150°, AC = 6. Найдите расстояние от вершины A до этой плоскости.

Упражнение 11Дан квадрат ABCD, через вершину D параллельно диагонали AC проведена плоскость α, образующая с диагональю BD угол 60°. Чему равен угол между плоскостью квадрата и плоскостью α?

Упражнение 12Основанием высоты четырехугольной пирамиды является точка пересечения диагоналей основания пирамиды. Верно ли, что двугранные углы, образованные боковыми гранями пирамиды с плоскостью основания, равны, если основанием пирамиды является: а) квадрат; б) параллелограмм; в) ромб; г) равнобедренная трапеция?

Упражнение 13В основании прямой призмы параллелограмм со сторонами 4 дм и 5 дм. Угол между ними 30°. Найдите площадь сечения призмы плоскостью, если известно, что она пересекает все боковые ребра и образует с плоскостью основания угол 45°.

Упражнение 14Боковое ребро прямой призмы равно 6 см. Ее основание – прямоугольный треугольник с катетами 3 см и 2 см. Найдите площади сечений призмы плоскостями, проходящими через каждый из данных катетов и образующими углы 60° с плоскостью основания.

Упражнение 15Сторона основания правильной треугольной призмы равна 4 см. Найдите площадь сечения призмы плоскостью, проходящей через середины двух сторон основания и образующей угол 45° с его плоскостью, если известно, что плоскость пересекает: а) только одно боковое ребро призмы; б) два ее боковых ребра.

Упражнение 16Ребро куба равно a. Найдите площадь сечения куба плоскостью, проходящей через сторону основания, если угол между этой плоскостью и плоскостью основания равен: а) 30°; б) .

Упражнение 17Через середины двух смежных сторон основания правильной четырехугольной призмы проведена плоскость, образующая с плоскостью основания угол и пересекающая три боковых ребра призмы. Найдите сторону основания, если площадь сечения равна Q.

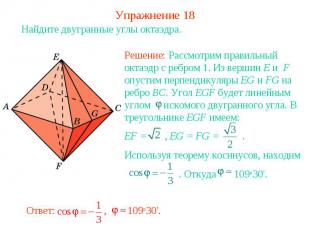
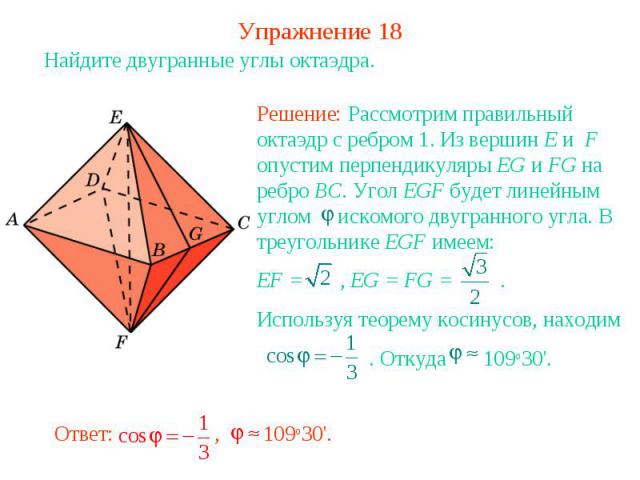
Упражнение 18Найдите двугранные углы октаэдра.Решение: Рассмотрим правильный октаэдр с ребром 1. Из вершин E и F опустим перпендикуляры EG и FG на ребро BC. Угол EGF будет линейным углом искомого двугранного угла. В треугольнике EGF имеем:EF = , EG = FG = . Используя теорему косинусов, находим . Откуда 109о30'.

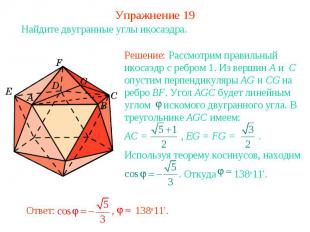
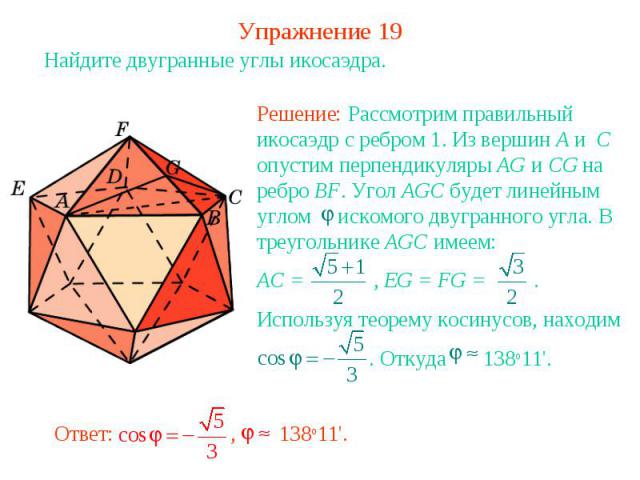
Упражнение 19Найдите двугранные углы икосаэдра.Решение: Рассмотрим правильный икосаэдр с ребром 1. Из вершин A и C опустим перпендикуляры AG и CG на ребро BF. Угол AGC будет линейным углом искомого двугранного угла. В треугольнике AGC имеем:AC = , EG = FG = . Используя теорему косинусов, находим . Откуда 138о11'.

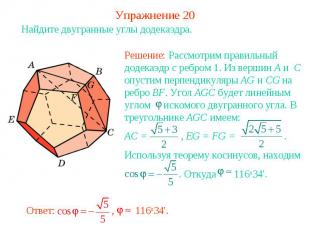
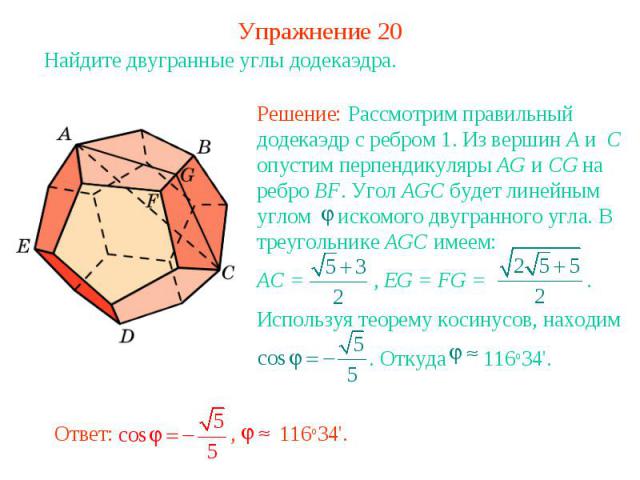
Упражнение 20Найдите двугранные углы додекаэдра.Решение: Рассмотрим правильный додекаэдр с ребром 1. Из вершин A и C опустим перпендикуляры AG и CG на ребро BF. Угол AGC будет линейным углом искомого двугранного угла. В треугольнике AGC имеем:AC = , EG = FG = . Используя теорему косинусов, находим . Откуда 116о34'.